Layer-wise Learning of Kernel Dependence Networks

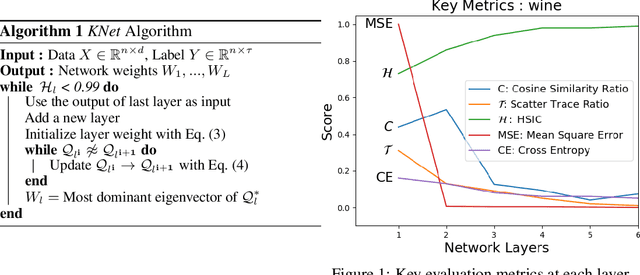
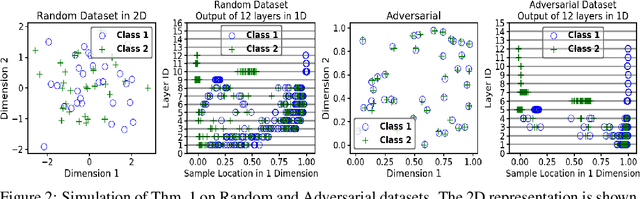
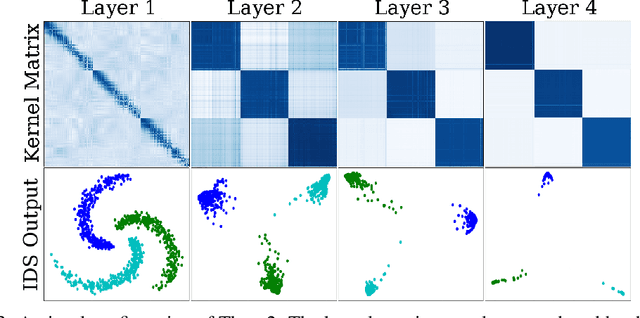
We propose a greedy strategy to train a deep network for multi-class classification, where each layer is defined as a composition of a linear projection and a nonlinear mapping. This nonlinear mapping is defined as the feature map of a Gaussian kernel, and the linear projection is learned by maximizing the dependence between the layer output and the labels, using the Hilbert Schmidt Independence Criterion (HSIC) as the dependence measure. Since each layer is trained greedily in sequence, all learning is local, and neither backpropagation nor even gradient descent is needed. The depth and width of the network are determined via natural guidelines, and the procedure regularizes its weights in the linear layer. As the key theoretical result, the function class represented by the network is proved to be sufficiently rich to learn any dataset labeling using a finite number of layers, in the sense of reaching minimum mean-squared error or cross-entropy, as long as no two data points with different labels coincide. Experiments demonstrate good generalization performance of the greedy approach across multiple benchmarks while showing a significant computational advantage against a multilayer perceptron of the same complexity trained globally by backpropagation.