3D-HGS: 3D Half-Gaussian Splatting

Photo-realistic 3D Reconstruction is a fundamental problem in 3D computer vision. This domain has seen considerable advancements owing to the advent of recent neural rendering techniques. These techniques predominantly aim to focus on learning volumetric representations of 3D scenes and refining these representations via loss functions derived from rendering. Among these, 3D Gaussian Splatting (3D-GS) has emerged as a significant method, surpassing Neural Radiance Fields (NeRFs). 3D-GS uses parameterized 3D Gaussians for modeling both spatial locations and color information, combined with a tile-based fast rendering technique. Despite its superior rendering performance and speed, the use of 3D Gaussian kernels has inherent limitations in accurately representing discontinuous functions, notably at edges and corners for shape discontinuities, and across varying textures for color discontinuities. To address this problem, we propose to employ 3D Half-Gaussian (3D-HGS) kernels, which can be used as a plug-and-play kernel. Our experiments demonstrate their capability to improve the performance of current 3D-GS related methods and achieve state-of-the-art rendering performance on various datasets without compromising rendering speed.

Solving Masked Jigsaw Puzzles with Diffusion Vision Transformers

Solving image and video jigsaw puzzles poses the challenging task of rearranging image fragments or video frames from unordered sequences to restore meaningful images and video sequences. Existing approaches often hinge on discriminative models tasked with predicting either the absolute positions of puzzle elements or the permutation actions applied to the original data. Unfortunately, these methods face limitations in effectively solving puzzles with a large number of elements. In this paper, we propose JPDVT, an innovative approach that harnesses diffusion transformers to address this challenge. Specifically, we generate positional information for image patches or video frames, conditioned on their underlying visual content. This information is then employed to accurately assemble the puzzle pieces in their correct positions, even in scenarios involving missing pieces. Our method achieves state-of-the-art performance on several datasets.

On the Hardness of Learning to Stabilize Linear Systems

Inspired by the work of Tsiamis et al. \cite{tsiamis2022learning}, in this paper we study the statistical hardness of learning to stabilize linear time-invariant systems. Hardness is measured by the number of samples required to achieve a learning task with a given probability. The work in \cite{tsiamis2022learning} shows that there exist system classes that are hard to learn to stabilize with the core reason being the hardness of identification. Here we present a class of systems that can be easy to identify, thanks to a non-degenerate noise process that excites all modes, but the sample complexity of stabilization still increases exponentially with the system dimension. We tie this result to the hardness of co-stabilizability for this class of systems using ideas from robust control.

Inferring Relational Potentials in Interacting Systems

Systems consisting of interacting agents are prevalent in the world, ranging from dynamical systems in physics to complex biological networks. To build systems which can interact robustly in the real world, it is thus important to be able to infer the precise interactions governing such systems. Existing approaches typically discover such interactions by explicitly modeling the feed-forward dynamics of the trajectories. In this work, we propose Neural Interaction Inference with Potentials (NIIP) as an alternative approach to discover such interactions that enables greater flexibility in trajectory modeling: it discovers a set of relational potentials, represented as energy functions, which when minimized reconstruct the original trajectory. NIIP assigns low energy to the subset of trajectories which respect the relational constraints observed. We illustrate that with these representations NIIP displays unique capabilities in test-time. First, it allows trajectory manipulation, such as interchanging interaction types across separately trained models, as well as trajectory forecasting. Additionally, it allows adding external hand-crafted potentials at test-time. Finally, NIIP enables the detection of out-of-distribution samples and anomalies without explicit training. Website: https://energy-based-model.github.io/interaction-potentials.

Cross-view Action Recognition via Contrastive View-invariant Representation

Cross view action recognition (CVAR) seeks to recognize a human action when observed from a previously unseen viewpoint. This is a challenging problem since the appearance of an action changes significantly with the viewpoint. Applications of CVAR include surveillance and monitoring of assisted living facilities where is not practical or feasible to collect large amounts of training data when adding a new camera. We present a simple yet efficient CVAR framework to learn invariant features from either RGB videos, 3D skeleton data, or both. The proposed approach outperforms the current state-of-the-art achieving similar levels of performance across input modalities: 99.4% (RGB) and 99.9% (3D skeletons), 99.4% (RGB) and 99.9% (3D Skeletons), 97.3% (RGB), and 99.2% (3D skeletons), and 84.4%(RGB) for the N-UCLA, NTU-RGB+D 60, NTU-RGB+D 120, and UWA3DII datasets, respectively.

SAIF: Sparse Adversarial and Interpretable Attack Framework

Adversarial attacks hamper the decision-making ability of neural networks by perturbing the input signal. The addition of calculated small distortion to images, for instance, can deceive a well-trained image classification network. In this work, we propose a novel attack technique called Sparse Adversarial and Interpretable Attack Framework (SAIF). Specifically, we design imperceptible attacks that contain low-magnitude perturbations at a small number of pixels and leverage these sparse attacks to reveal the vulnerability of classifiers. We use the Frank-Wolfe (conditional gradient) algorithm to simultaneously optimize the attack perturbations for bounded magnitude and sparsity with $O(1/\sqrt{T})$ convergence. Empirical results show that SAIF computes highly imperceptible and interpretable adversarial examples, and outperforms state-of-the-art sparse attack methods on the ImageNet dataset.

Self-Supervised Decomposition, Disentanglement and Prediction of Video Sequences while Interpreting Dynamics: A Koopman Perspective

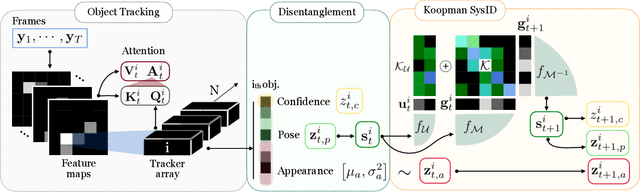
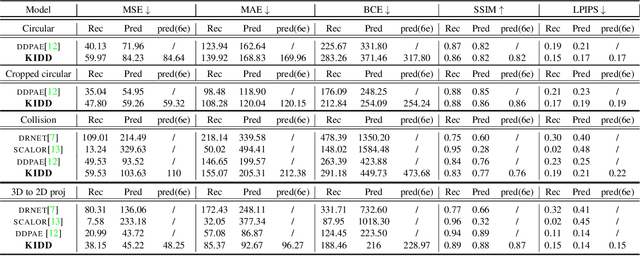
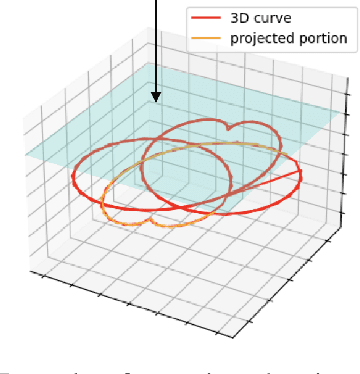
Human interpretation of the world encompasses the use of symbols to categorize sensory inputs and compose them in a hierarchical manner. One of the long-term objectives of Computer Vision and Artificial Intelligence is to endow machines with the capacity of structuring and interpreting the world as we do. Towards this goal, recent methods have successfully been able to decompose and disentangle video sequences into their composing objects and dynamics, in a self-supervised fashion. However, there has been a scarce effort in giving interpretation to the dynamics of the scene. We propose a method to decompose a video into moving objects and their attributes, and model each object's dynamics with linear system identification tools, by means of a Koopman embedding. This allows interpretation, manipulation and extrapolation of the dynamics of the different objects by employing the Koopman operator K. We test our method in various synthetic datasets and successfully forecast challenging trajectories while interpreting them.

Key Frame Proposal Network for Efficient Pose Estimation in Videos

Human pose estimation in video relies on local information by either estimating each frame independently or tracking poses across frames. In this paper, we propose a novel method combining local approaches with global context. We introduce a light weighted, unsupervised, key frame proposal network (K-FPN) to select informative frames and a learned dictionary to recover the entire pose sequence from these frames. The K-FPN speeds up the pose estimation and provides robustness to bad frames with occlusion, motion blur, and illumination changes, while the learned dictionary provides global dynamic context. Experiments on Penn Action and sub-JHMDB datasets show that the proposed method achieves state-of-the-art accuracy, with substantial speed-up.

Solving Interpretable Kernel Dimension Reduction

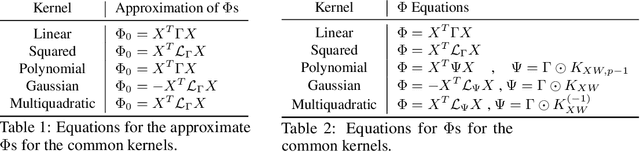
Kernel dimensionality reduction (KDR) algorithms find a low dimensional representation of the original data by optimizing kernel dependency measures that are capable of capturing nonlinear relationships. The standard strategy is to first map the data into a high dimensional feature space using kernels prior to a projection onto a low dimensional space. While KDR methods can be easily solved by keeping the most dominant eigenvectors of the kernel matrix, its features are no longer easy to interpret. Alternatively, Interpretable KDR (IKDR) is different in that it projects onto a subspace \textit{before} the kernel feature mapping, therefore, the projection matrix can indicate how the original features linearly combine to form the new features. Unfortunately, the IKDR objective requires a non-convex manifold optimization that is difficult to solve and can no longer be solved by eigendecomposition. Recently, an efficient iterative spectral (eigendecomposition) method (ISM) has been proposed for this objective in the context of alternative clustering. However, ISM only provides theoretical guarantees for the Gaussian kernel. This greatly constrains ISM's usage since any kernel method using ISM is now limited to a single kernel. This work extends the theoretical guarantees of ISM to an entire family of kernels, thereby empowering ISM to solve any kernel method of the same objective. In identifying this family, we prove that each kernel within the family has a surrogate $\Phi$ matrix and the optimal projection is formed by its most dominant eigenvectors. With this extension, we establish how a wide range of IKDR applications across different learning paradigms can be solved by ISM. To support reproducible results, the source code is made publicly available on \url{https://github.com/chieh-neu/ISM_supervised_DR}.

Iterative Spectral Method for Alternative Clustering

Given a dataset and an existing clustering as input, alternative clustering aims to find an alternative partition. One of the state-of-the-art approaches is Kernel Dimension Alternative Clustering (KDAC). We propose a novel Iterative Spectral Method (ISM) that greatly improves the scalability of KDAC. Our algorithm is intuitive, relies on easily implementable spectral decompositions, and comes with theoretical guarantees. Its computation time improves upon existing implementations of KDAC by as much as 5 orders of magnitude.