On the Hardness of Learning to Stabilize Linear Systems

Inspired by the work of Tsiamis et al. \cite{tsiamis2022learning}, in this paper we study the statistical hardness of learning to stabilize linear time-invariant systems. Hardness is measured by the number of samples required to achieve a learning task with a given probability. The work in \cite{tsiamis2022learning} shows that there exist system classes that are hard to learn to stabilize with the core reason being the hardness of identification. Here we present a class of systems that can be easy to identify, thanks to a non-degenerate noise process that excites all modes, but the sample complexity of stabilization still increases exponentially with the system dimension. We tie this result to the hardness of co-stabilizability for this class of systems using ideas from robust control.

Can Transformers Learn Optimal Filtering for Unknown Systems?

Transformers have demonstrated remarkable success in natural language processing; however, their potential remains mostly unexplored for problems arising in dynamical systems. In this work, we investigate the optimal output estimation problem using transformers, which generate output predictions using all the past ones. We train the transformer using various systems drawn from a prior distribution and then evaluate its performance on previously unseen systems from the same distribution. As a result, the obtained transformer acts like a prediction algorithm that learns in-context and quickly adapts to and predicts well for different systems - thus we call it meta-output-predictor (MOP). MOP matches the performance of the optimal output estimator, based on Kalman filter, for most linear dynamical systems even though it does not have access to a model. We observe via extensive numerical experiments that MOP also performs well in challenging scenarios with non-i.i.d. noise, time-varying dynamics, and nonlinear dynamics like a quadrotor system with unknown parameters. To further support this observation, in the second part of the paper, we provide statistical guarantees on the performance of MOP and quantify the required amount of training to achieve a desired excess risk during test-time. Finally, we point out some limitations of MOP by identifying two classes of problems MOP fails to perform well, highlighting the need for caution when using transformers for control and estimation.

Mode Reduction for Markov Jump Systems

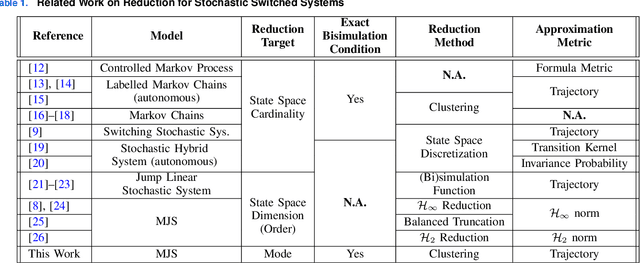
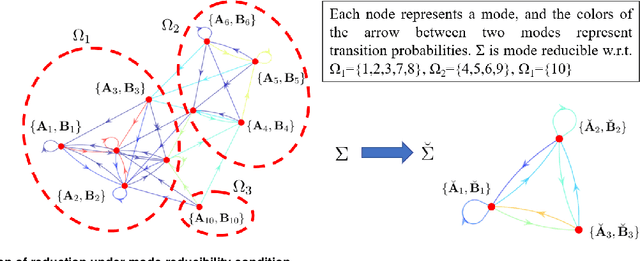
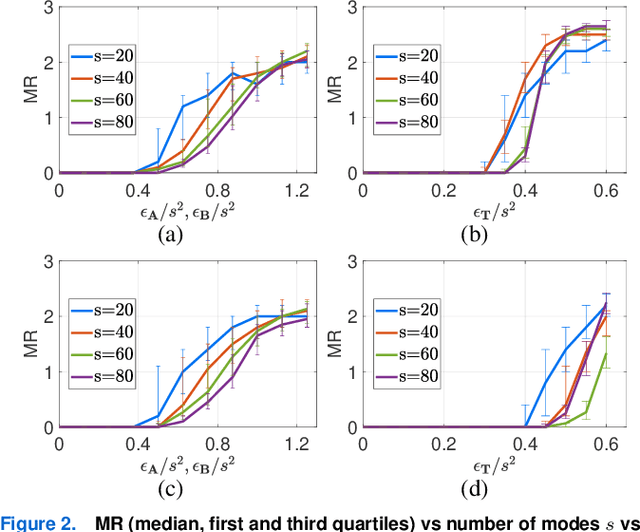
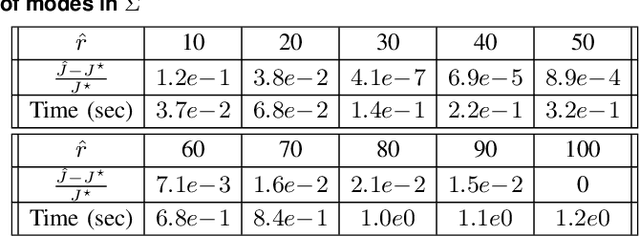
Switched systems are capable of modeling processes with underlying dynamics that may change abruptly over time. To achieve accurate modeling in practice, one may need a large number of modes, but this may in turn increase the model complexity drastically. Existing work on reducing system complexity mainly considers state space reduction, yet reducing the number of modes is less studied. In this work, we consider Markov jump linear systems (MJSs), a special class of switched systems where the active mode switches according to a Markov chain, and several issues associated with its mode complexity. Specifically, inspired by clustering techniques from unsupervised learning, we are able to construct a reduced MJS with fewer modes that approximates well the original MJS under various metrics. Furthermore, both theoretically and empirically, we show how one can use the reduced MJS to analyze stability and design controllers with significant reduction in computational cost while achieving guaranteed accuracy.

A Circle Grid-based Approach for Obstacle Avoidance Motion Planning of Unmanned Surface Vehicles

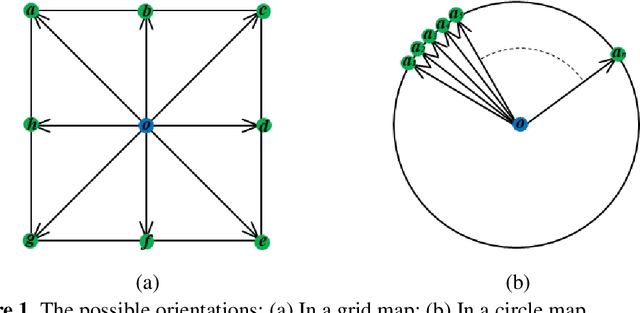
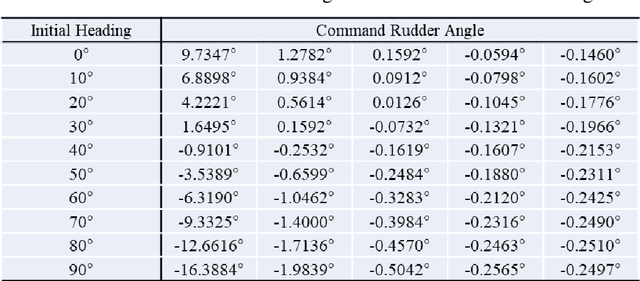
Aiming at an obstacle avoidance problem with dynamic constraints for Unmanned Surface Vehicle (USV), a method based on Circle Grid Trajectory Cell (CGTC) is proposed. Firstly, the ship model and standardization rules are constructed to develop and constrain the trajectory, respectively. Secondly, by analyzing the properties of the circle grid, the circle grid tree is produced to guide the motion of the USV. Then, the kinematics and dynamics of the USV are considered through the on-line trajectory generator by designing a relational function that links the rudder angle, heading angle, and the central angle of the circle grid. Finally, obstacle avoidance is achieved by leveraging the on-line trajectory generator to choose a safe, smooth, and efficient path for the USV. The experimental results indicate that the proposed method can avoid both static and dynamic obstacles, have better performance in terms of distance cost and steering cost comparing with the related methods, and our method only takes 50% steering cost of the grid-based method; the collision avoidance path not only conforms to the USV dynamic characteristic but also provides a reference of steering command.

Identification and Adaptive Control of Markov Jump Systems: Sample Complexity and Regret Bounds

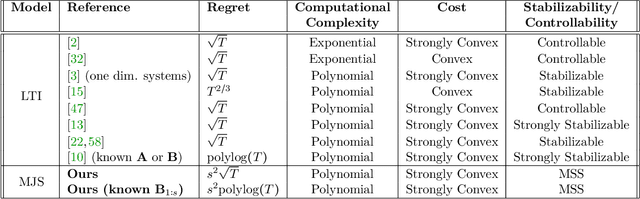
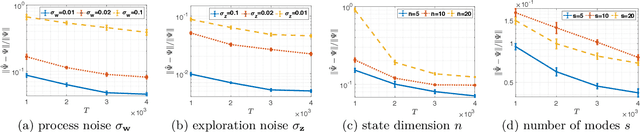
Learning how to effectively control unknown dynamical systems is crucial for intelligent autonomous systems. This task becomes a significant challenge when the underlying dynamics are changing with time. Motivated by this challenge, this paper considers the problem of controlling an unknown Markov jump linear system (MJS) to optimize a quadratic objective. By taking a model-based perspective, we consider identification-based adaptive control for MJSs. We first provide a system identification algorithm for MJS to learn the dynamics in each mode as well as the Markov transition matrix, underlying the evolution of the mode switches, from a single trajectory of the system states, inputs, and modes. Through mixing-time arguments, sample complexity of this algorithm is shown to be $\mathcal{O}(1/\sqrt{T})$. We then propose an adaptive control scheme that performs system identification together with certainty equivalent control to adapt the controllers in an episodic fashion. Combining our sample complexity results with recent perturbation results for certainty equivalent control, we prove that when the episode lengths are appropriately chosen, the proposed adaptive control scheme achieves $\mathcal{O}(\sqrt{T})$ regret, which can be improved to $\mathcal{O}(polylog(T))$ with partial knowledge of the system. Our proof strategy introduces innovations to handle Markovian jumps and a weaker notion of stability common in MJSs. Our analysis provides insights into system theoretic quantities that affect learning accuracy and control performance. Numerical simulations are presented to further reinforce these insights.

Certainty Equivalent Quadratic Control for Markov Jump Systems

Real-world control applications often involve complex dynamics subject to abrupt changes or variations. Markov jump linear systems (MJS) provide a rich framework for modeling such dynamics. Despite an extensive history, theoretical understanding of parameter sensitivities of MJS control is somewhat lacking. Motivated by this, we investigate robustness aspects of certainty equivalent model-based optimal control for MJS with quadratic cost function. Given the uncertainty in the system matrices and in the Markov transition matrix is bounded by $\epsilon$ and $\eta$ respectively, robustness results are established for (i) the solution to coupled Riccati equations and (ii) the optimal cost, by providing explicit perturbation bounds which decay as $\mathcal{O}(\epsilon + \eta)$ and $\mathcal{O}((\epsilon + \eta)^2)$ respectively.

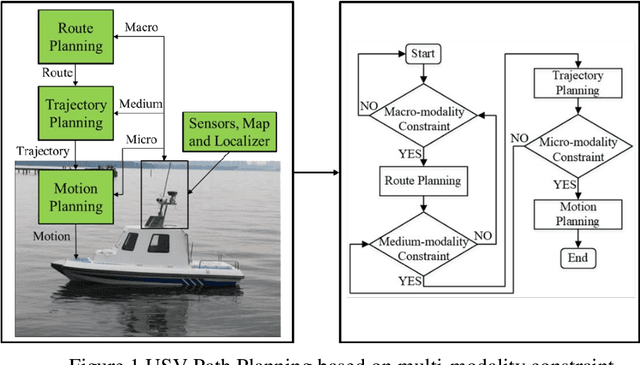
The Review Unmanned Surface Vehicle Path Planning: Based on Multi-modality Constraint

The essence of the path planning problems is multi-modality constraint. However, most of the current literature has not mentioned this issue. This paper introduces the research progress of path planning based on the multi-modality constraint. The path planning of multi-modality constraint research can be classified into three stages in terms of its basic ingredients (such as shape, kinematics and dynamics et al.): Route Planning, Trajectory Planning and Motion Planning. It then reviews the research methods and classical algorithms, especially those applied to the Unmanned Surface Vehicle (USV) in every stage. Finally, the paper points out some existing problems in every stage and suggestions for future research.