Identification and Adaptive Control of Markov Jump Systems: Sample Complexity and Regret Bounds

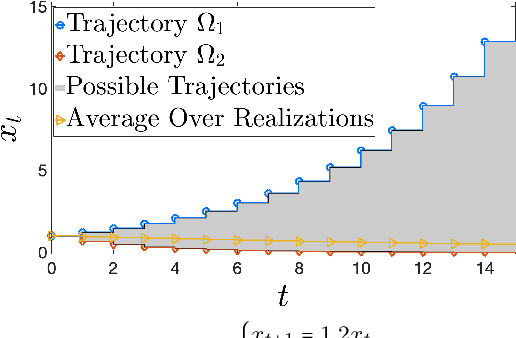
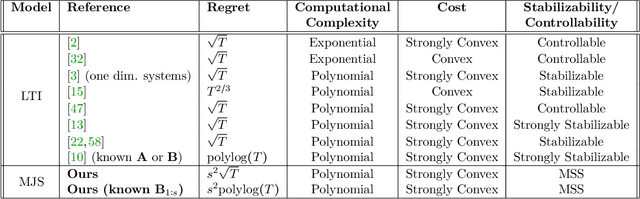
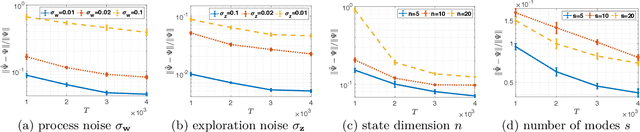
Learning how to effectively control unknown dynamical systems is crucial for intelligent autonomous systems. This task becomes a significant challenge when the underlying dynamics are changing with time. Motivated by this challenge, this paper considers the problem of controlling an unknown Markov jump linear system (MJS) to optimize a quadratic objective. By taking a model-based perspective, we consider identification-based adaptive control for MJSs. We first provide a system identification algorithm for MJS to learn the dynamics in each mode as well as the Markov transition matrix, underlying the evolution of the mode switches, from a single trajectory of the system states, inputs, and modes. Through mixing-time arguments, sample complexity of this algorithm is shown to be $\mathcal{O}(1/\sqrt{T})$. We then propose an adaptive control scheme that performs system identification together with certainty equivalent control to adapt the controllers in an episodic fashion. Combining our sample complexity results with recent perturbation results for certainty equivalent control, we prove that when the episode lengths are appropriately chosen, the proposed adaptive control scheme achieves $\mathcal{O}(\sqrt{T})$ regret, which can be improved to $\mathcal{O}(polylog(T))$ with partial knowledge of the system. Our proof strategy introduces innovations to handle Markovian jumps and a weaker notion of stability common in MJSs. Our analysis provides insights into system theoretic quantities that affect learning accuracy and control performance. Numerical simulations are presented to further reinforce these insights.