Ankle Exoskeletons May Hinder Standing Balance in Simple Models of Older and Younger Adults

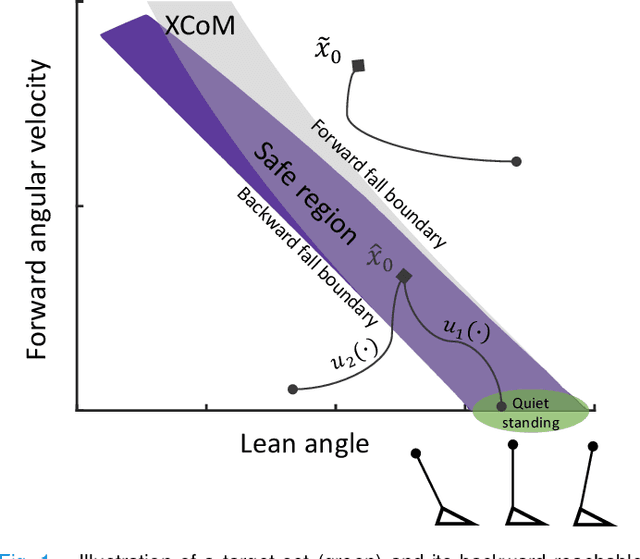
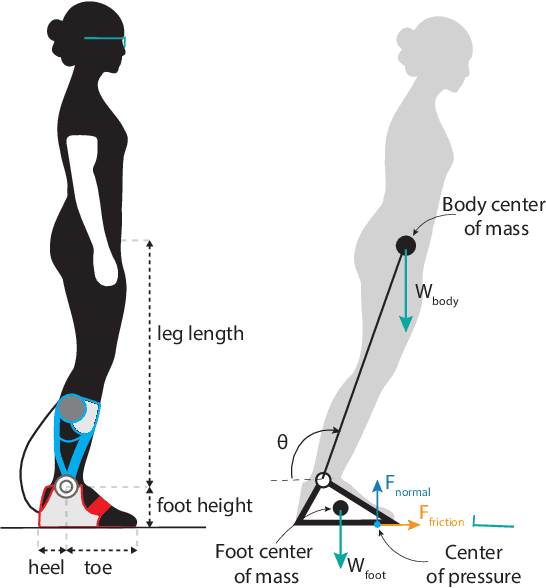
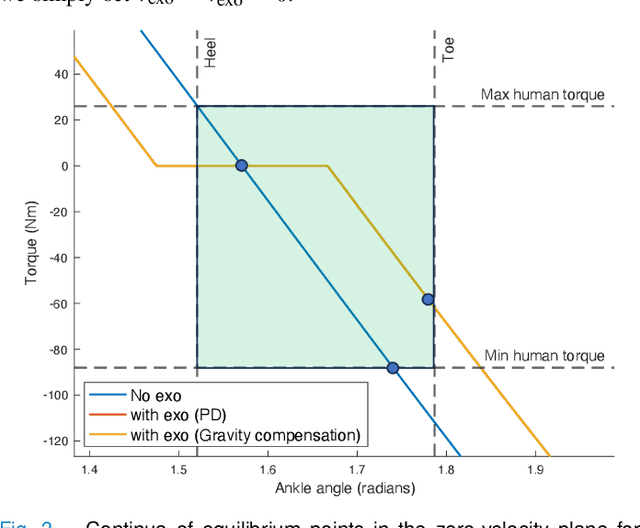
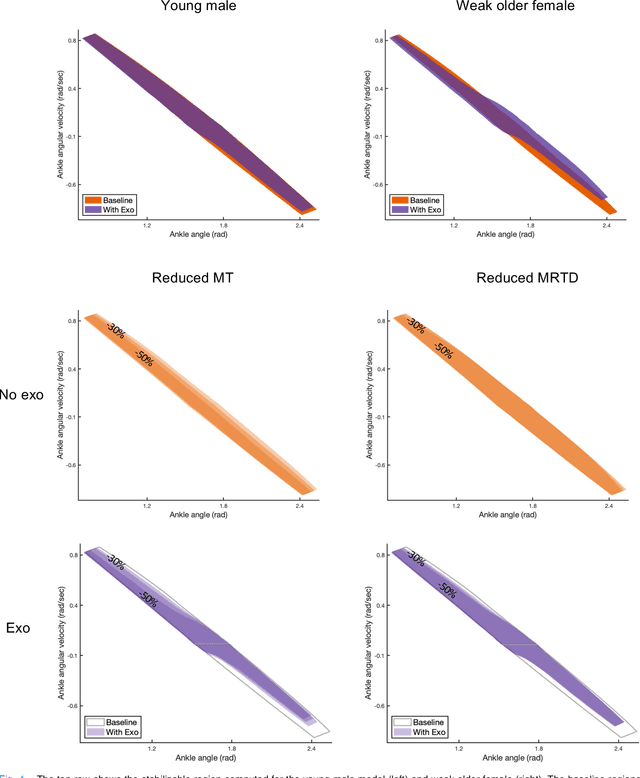
Humans rely on ankle torque to maintain standing balance, particularly in the presence of small to moderate perturbations. Reductions in maximum torque (MT) production and maximum rate of torque development (MRTD) occur at the ankle with age, diminishing stability. Ankle exoskeletons are powered orthotic devices that may assist older adults by compensating for reduced muscle force and power production capabilities. They may also be able to assist with ankle strategies used for balance. However, no studies have investigated the effect of such devices on balance in older adults. Here, we model the effect ankle exoskeletons have on stability in physics-based models of healthy young and old adults, focusing on the mitigation of age-related deficits such as reduced MT and MRTD. We show that an ankle exoskeleton moderately reduces feasible stability boundaries in users who have full ankle strength. For individuals with age-related deficits, there is a trade-off. While exoskeletons augment stability in low velocity conditions, they reduce stability in some high velocity conditions. Our results suggest that well-established control strategies must still be experimentally validated in older adults.

On the Hardness of Learning to Stabilize Linear Systems

Inspired by the work of Tsiamis et al. \cite{tsiamis2022learning}, in this paper we study the statistical hardness of learning to stabilize linear time-invariant systems. Hardness is measured by the number of samples required to achieve a learning task with a given probability. The work in \cite{tsiamis2022learning} shows that there exist system classes that are hard to learn to stabilize with the core reason being the hardness of identification. Here we present a class of systems that can be easy to identify, thanks to a non-degenerate noise process that excites all modes, but the sample complexity of stabilization still increases exponentially with the system dimension. We tie this result to the hardness of co-stabilizability for this class of systems using ideas from robust control.

A Preference Learning Approach to Develop Safe and Personalizable Autonomous Vehicles

This work introduces a preference learning method that ensures adherence to traffic rules for autonomous vehicles. Our approach incorporates priority ordering of signal temporal logic (STL) formulas, describing traffic rules, into a learning framework. By leveraging the parametric weighted signal temporal logic (PWSTL), we formulate the problem of safety-guaranteed preference learning based on pairwise comparisons, and propose an approach to solve this learning problem. Our approach finds a feasible valuation for the weights of the given PWSTL formula such that, with these weights, preferred signals have weighted quantitative satisfaction measures greater than their non-preferred counterparts. The feasible valuation of weights given by our approach leads to a weighted STL formula which can be used in correct-and-custom-by-construction controller synthesis. We demonstrate the performance of our method with human subject studies in two different simulated driving scenarios involving a stop sign and a pedestrian crossing. Our approach yields competitive results compared to existing preference learning methods in terms of capturing preferences, and notably outperforms them when safety is considered.

Can Transformers Learn Optimal Filtering for Unknown Systems?

Transformers have demonstrated remarkable success in natural language processing; however, their potential remains mostly unexplored for problems arising in dynamical systems. In this work, we investigate the optimal output estimation problem using transformers, which generate output predictions using all the past ones. We train the transformer using various systems drawn from a prior distribution and then evaluate its performance on previously unseen systems from the same distribution. As a result, the obtained transformer acts like a prediction algorithm that learns in-context and quickly adapts to and predicts well for different systems - thus we call it meta-output-predictor (MOP). MOP matches the performance of the optimal output estimator, based on Kalman filter, for most linear dynamical systems even though it does not have access to a model. We observe via extensive numerical experiments that MOP also performs well in challenging scenarios with non-i.i.d. noise, time-varying dynamics, and nonlinear dynamics like a quadrotor system with unknown parameters. To further support this observation, in the second part of the paper, we provide statistical guarantees on the performance of MOP and quantify the required amount of training to achieve a desired excess risk during test-time. Finally, we point out some limitations of MOP by identifying two classes of problems MOP fails to perform well, highlighting the need for caution when using transformers for control and estimation.

Falsification of a Vision-based Automatic Landing System

At smaller airports without an instrument approach or advanced equipment, automatic landing of aircraft is a safety-critical task that requires the use of sensors present on the aircraft. In this paper, we study falsification of an automatic landing system for fixed-wing aircraft using a camera as its main sensor. We first present an architecture for vision-based automatic landing, including a vision-based runway distance and orientation estimator and an associated PID controller. We then outline landing specifications that we validate with actual flight data. Using these specifications, we propose the use of the falsification tool Breach to find counterexamples to the specifications in the automatic landing system. Our experiments are implemented using a Beechcraft Baron 58 in the X-Plane flight simulator communicating with MATLAB Simulink.

Finite Sample Identification of Bilinear Dynamical Systems

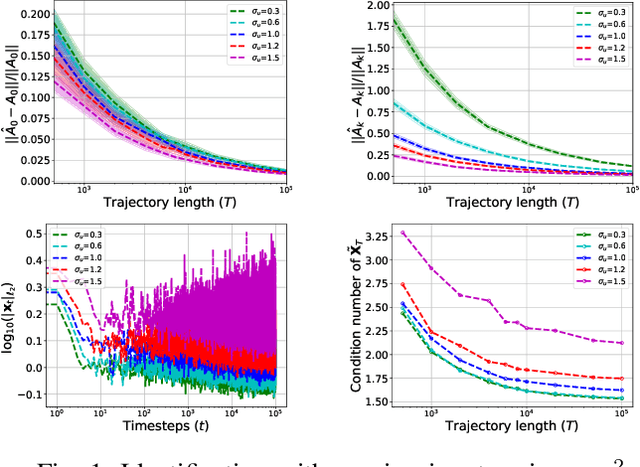
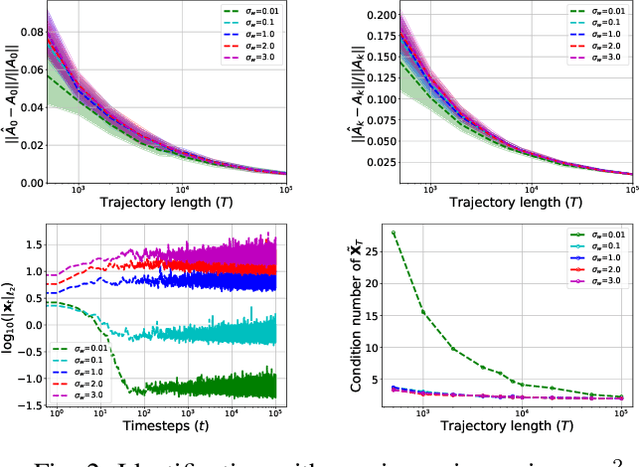
Bilinear dynamical systems are ubiquitous in many different domains and they can also be used to approximate more general control-affine systems. This motivates the problem of learning bilinear systems from a single trajectory of the system's states and inputs. Under a mild marginal mean-square stability assumption, we identify how much data is needed to estimate the unknown bilinear system up to a desired accuracy with high probability. Our sample complexity and statistical error rates are optimal in terms of the trajectory length, the dimensionality of the system and the input size. Our proof technique relies on an application of martingale small-ball condition. This enables us to correctly capture the properties of the problem, specifically our error rates do not deteriorate with increasing instability. Finally, we show that numerical experiments are well-aligned with our theoretical results.

Safe Output Feedback Motion Planning from Images via Learned Perception Modules and Contraction Theory

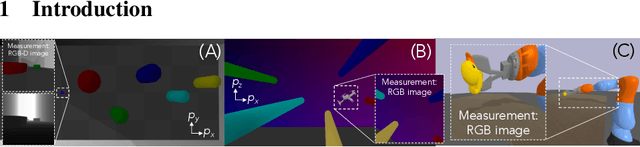
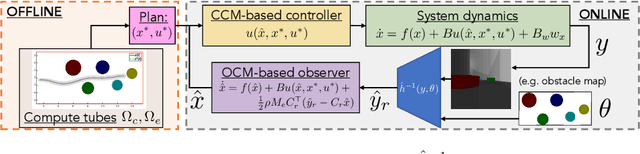
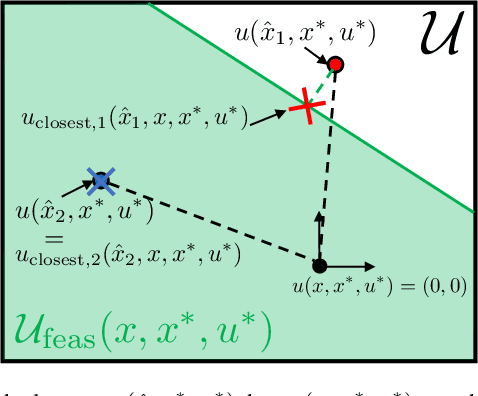
We present a motion planning algorithm for a class of uncertain control-affine nonlinear systems which guarantees runtime safety and goal reachability when using high-dimensional sensor measurements (e.g., RGB-D images) and a learned perception module in the feedback control loop. First, given a dataset of states and observations, we train a perception system that seeks to invert a subset of the state from an observation, and estimate an upper bound on the perception error which is valid with high probability in a trusted domain near the data. Next, we use contraction theory to design a stabilizing state feedback controller and a convergent dynamic state observer which uses the learned perception system to update its state estimate. We derive a bound on the trajectory tracking error when this controller is subjected to errors in the dynamics and incorrect state estimates. Finally, we integrate this bound into a sampling-based motion planner, guiding it to return trajectories that can be safely tracked at runtime using sensor data. We demonstrate our approach in simulation on a 4D car, a 6D planar quadrotor, and a 17D manipulation task with RGB(-D) sensor measurements, demonstrating that our method safely and reliably steers the system to the goal, while baselines that fail to consider the trusted domain or state estimation errors can be unsafe.

Mode Reduction for Markov Jump Systems

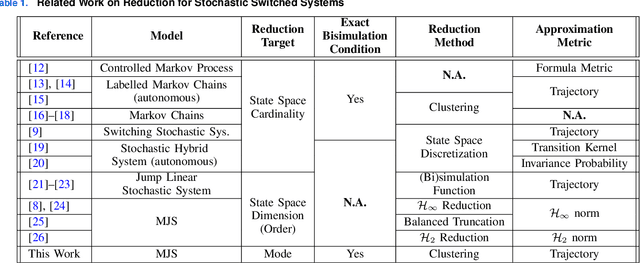
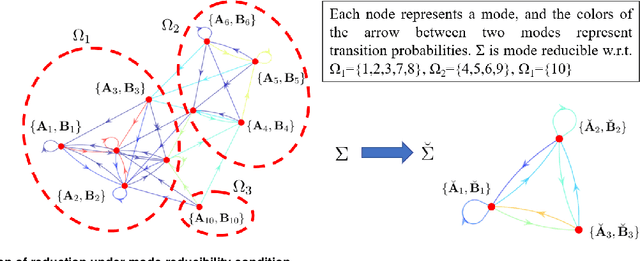
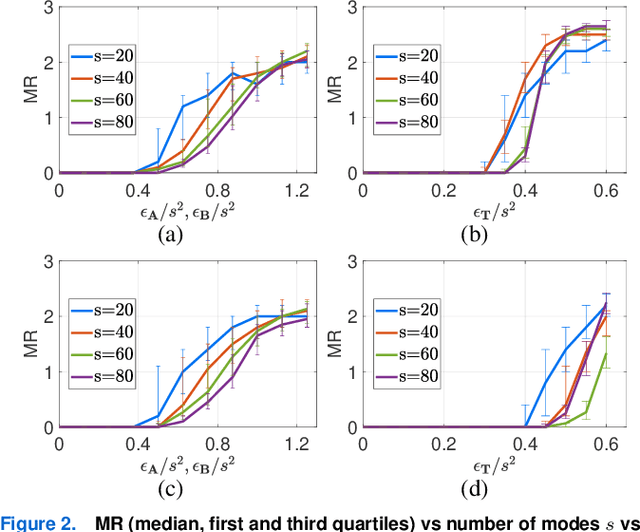
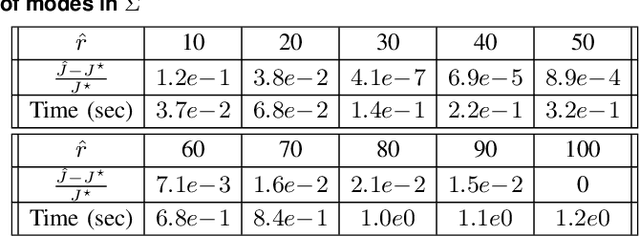
Switched systems are capable of modeling processes with underlying dynamics that may change abruptly over time. To achieve accurate modeling in practice, one may need a large number of modes, but this may in turn increase the model complexity drastically. Existing work on reducing system complexity mainly considers state space reduction, yet reducing the number of modes is less studied. In this work, we consider Markov jump linear systems (MJSs), a special class of switched systems where the active mode switches according to a Markov chain, and several issues associated with its mode complexity. Specifically, inspired by clustering techniques from unsupervised learning, we are able to construct a reduced MJS with fewer modes that approximates well the original MJS under various metrics. Furthermore, both theoretically and empirically, we show how one can use the reduced MJS to analyze stability and design controllers with significant reduction in computational cost while achieving guaranteed accuracy.

Identification and Adaptive Control of Markov Jump Systems: Sample Complexity and Regret Bounds

Learning how to effectively control unknown dynamical systems is crucial for intelligent autonomous systems. This task becomes a significant challenge when the underlying dynamics are changing with time. Motivated by this challenge, this paper considers the problem of controlling an unknown Markov jump linear system (MJS) to optimize a quadratic objective. By taking a model-based perspective, we consider identification-based adaptive control for MJSs. We first provide a system identification algorithm for MJS to learn the dynamics in each mode as well as the Markov transition matrix, underlying the evolution of the mode switches, from a single trajectory of the system states, inputs, and modes. Through mixing-time arguments, sample complexity of this algorithm is shown to be $\mathcal{O}(1/\sqrt{T})$. We then propose an adaptive control scheme that performs system identification together with certainty equivalent control to adapt the controllers in an episodic fashion. Combining our sample complexity results with recent perturbation results for certainty equivalent control, we prove that when the episode lengths are appropriately chosen, the proposed adaptive control scheme achieves $\mathcal{O}(\sqrt{T})$ regret, which can be improved to $\mathcal{O}(polylog(T))$ with partial knowledge of the system. Our proof strategy introduces innovations to handle Markovian jumps and a weaker notion of stability common in MJSs. Our analysis provides insights into system theoretic quantities that affect learning accuracy and control performance. Numerical simulations are presented to further reinforce these insights.

Certainty Equivalent Quadratic Control for Markov Jump Systems

Real-world control applications often involve complex dynamics subject to abrupt changes or variations. Markov jump linear systems (MJS) provide a rich framework for modeling such dynamics. Despite an extensive history, theoretical understanding of parameter sensitivities of MJS control is somewhat lacking. Motivated by this, we investigate robustness aspects of certainty equivalent model-based optimal control for MJS with quadratic cost function. Given the uncertainty in the system matrices and in the Markov transition matrix is bounded by $\epsilon$ and $\eta$ respectively, robustness results are established for (i) the solution to coupled Riccati equations and (ii) the optimal cost, by providing explicit perturbation bounds which decay as $\mathcal{O}(\epsilon + \eta)$ and $\mathcal{O}((\epsilon + \eta)^2)$ respectively.