Improving Out-of-Distribution Generalization of Learned Dynamics by Learning Pseudometrics and Constraint Manifolds

We propose a method for improving the prediction accuracy of learned robot dynamics models on out-of-distribution (OOD) states. We achieve this by leveraging two key sources of structure often present in robot dynamics: 1) sparsity, i.e., some components of the state may not affect the dynamics, and 2) physical limits on the set of possible motions, in the form of nonholonomic constraints. Crucially, we do not assume this structure is known a priori, and instead learn it from data. We use contrastive learning to obtain a distance pseudometric that uncovers the sparsity pattern in the dynamics, and use it to reduce the input space when learning the dynamics. We then learn the unknown constraint manifold by approximating the normal space of possible motions from the data, which we use to train a Gaussian process (GP) representation of the constraint manifold. We evaluate our approach on a physical differential-drive robot and a simulated quadrotor, showing improved prediction accuracy on OOD data relative to baselines.

Fighting Uncertainty with Gradients: Offline Reinforcement Learning via Diffusion Score Matching

Offline optimization paradigms such as offline Reinforcement Learning (RL) or Imitation Learning (IL) allow policy search algorithms to make use of offline data, but require careful incorporation of uncertainty in order to circumvent the challenges of distribution shift. Gradient-based policy search methods are a promising direction due to their effectiveness in high dimensions; however, we require a more careful consideration of how these methods interplay with uncertainty estimation. We claim that in order for an uncertainty metric to be amenable for gradient-based optimization, it must be (i) stably convergent to data when uncertainty is minimized with gradients, and (ii) not prone to underestimation of true uncertainty. We investigate smoothed distance to data as a metric, and show that it not only stably converges to data, but also allows us to analyze model bias with Lipschitz constants. Moreover, we establish an equivalence between smoothed distance to data and data likelihood, which allows us to use score-matching techniques to learn gradients of distance to data. Importantly, we show that offline model-based policy search problems that maximize data likelihood do not require values of likelihood; but rather only the gradient of the log likelihood (the score function). Using this insight, we propose Score-Guided Planning (SGP), a planning algorithm for offline RL that utilizes score-matching to enable first-order planning in high-dimensional problems, where zeroth-order methods were unable to scale, and ensembles were unable to overcome local minima. Website: https://sites.google.com/view/score-guided-planning/home

Synthesizing Stable Reduced-Order Visuomotor Policies for Nonlinear Systems via Sums-of-Squares Optimization

We present a method for synthesizing dynamic, reduced-order output-feedback polynomial control policies for control-affine nonlinear systems which guarantees runtime stability to a goal state, when using visual observations and a learned perception module in the feedback control loop. We leverage Lyapunov analysis to formulate the problem of synthesizing such policies. This problem is nonconvex in the policy parameters and the Lyapunov function that is used to prove the stability of the policy. To solve this problem approximately, we propose two approaches: the first solves a sequence of sum-of-squares optimization problems to iteratively improve a policy which is provably-stable by construction, while the second directly performs gradient-based optimization on the parameters of the polynomial policy, and its closed-loop stability is verified a posteriori. We extend our approach to provide stability guarantees in the presence of observation noise, which realistically arises due to errors in the learned perception module. We evaluate our approach on several underactuated nonlinear systems, including pendula and quadrotors, showing that our guarantees translate to empirical stability when controlling these systems from images, while baseline approaches can fail to reliably stabilize the system.

Data-Efficient Learning of Natural Language to Linear Temporal Logic Translators for Robot Task Specification

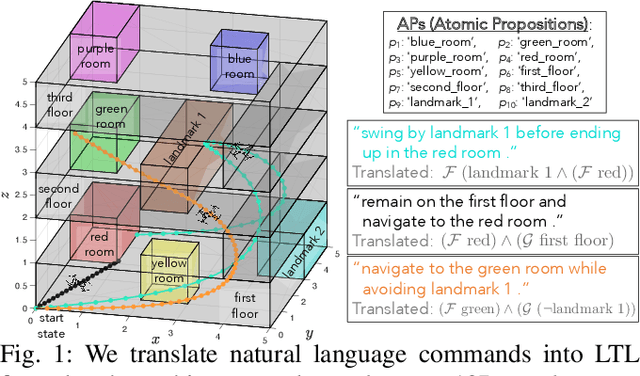
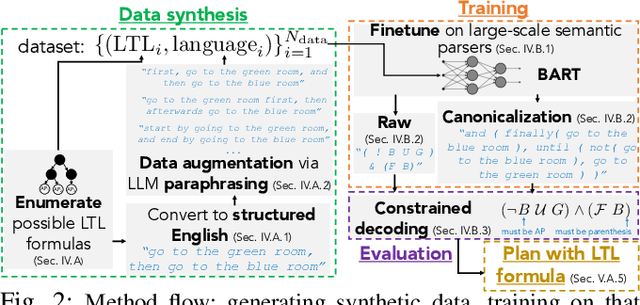
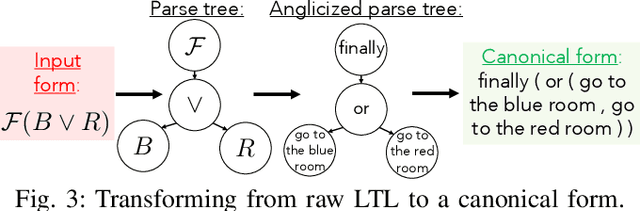
To make robots accessible to a broad audience, it is critical to endow them with the ability to take universal modes of communication, like commands given in natural language, and extract a concrete desired task specification, defined using a formal language like linear temporal logic (LTL). In this paper, we present a learning-based approach for translating from natural language commands to LTL specifications with very limited human-labeled training data. This is in stark contrast to existing natural-language to LTL translators, which require large human-labeled datasets, often in the form of labeled pairs of LTL formulas and natural language commands, to train the translator. To reduce reliance on human data, our approach generates a large synthetic training dataset through algorithmic generation of LTL formulas, conversion to structured English, and then exploiting the paraphrasing capabilities of modern large language models (LLMs) to synthesize a diverse corpus of natural language commands corresponding to the LTL formulas. We use this generated data to finetune an LLM and apply a constrained decoding procedure at inference time to ensure the returned LTL formula is syntactically correct. We evaluate our approach on three existing LTL/natural language datasets and show that we can translate natural language commands at 75\% accuracy with far less human data ($\le$12 annotations). Moreover, when training on large human-annotated datasets, our method achieves higher test accuracy (95\% on average) than prior work. Finally, we show the translated formulas can be used to plan long-horizon, multi-stage tasks on a 12D quadrotor.

Statistical Safety and Robustness Guarantees for Feedback Motion Planning of Unknown Underactuated Stochastic Systems

We present a method for providing statistical guarantees on runtime safety and goal reachability for integrated planning and control of a class of systems with unknown nonlinear stochastic underactuated dynamics. Specifically, given a dynamics dataset, our method jointly learns a mean dynamics model, a spatially-varying disturbance bound that captures the effect of noise and model mismatch, and a feedback controller based on contraction theory that stabilizes the learned dynamics. We propose a sampling-based planner that uses the mean dynamics model and simultaneously bounds the closed-loop tracking error via a learned disturbance bound. We employ techniques from Extreme Value Theory (EVT) to estimate, to a specified level of confidence, several constants which characterize the learned components and govern the size of the tracking error bound. This ensures plans are guaranteed to be safely tracked at runtime. We validate that our guarantees translate to empirical safety in simulation on a 10D quadrotor, and in the real world on a physical CrazyFlie quadrotor and Clearpath Jackal robot, whereas baselines that ignore the model error and stochasticity are unsafe.

Safe Output Feedback Motion Planning from Images via Learned Perception Modules and Contraction Theory

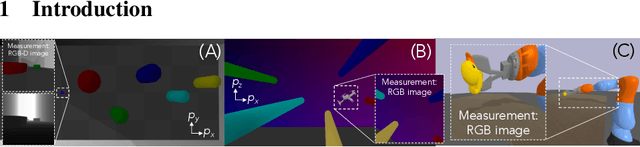
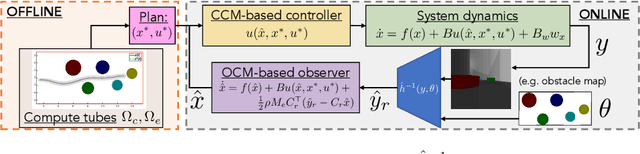
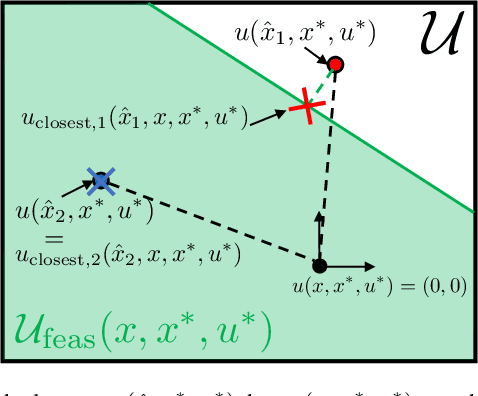
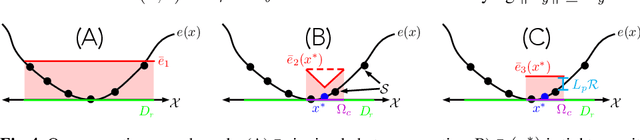
We present a motion planning algorithm for a class of uncertain control-affine nonlinear systems which guarantees runtime safety and goal reachability when using high-dimensional sensor measurements (e.g., RGB-D images) and a learned perception module in the feedback control loop. First, given a dataset of states and observations, we train a perception system that seeks to invert a subset of the state from an observation, and estimate an upper bound on the perception error which is valid with high probability in a trusted domain near the data. Next, we use contraction theory to design a stabilizing state feedback controller and a convergent dynamic state observer which uses the learned perception system to update its state estimate. We derive a bound on the trajectory tracking error when this controller is subjected to errors in the dynamics and incorrect state estimates. Finally, we integrate this bound into a sampling-based motion planner, guiding it to return trajectories that can be safely tracked at runtime using sensor data. We demonstrate our approach in simulation on a 4D car, a 6D planar quadrotor, and a 17D manipulation task with RGB(-D) sensor measurements, demonstrating that our method safely and reliably steers the system to the goal, while baselines that fail to consider the trusted domain or state estimation errors can be unsafe.

Gaussian Process Constraint Learning for Scalable Chance-Constrained Motion Planning from Demonstrations

We propose a method for learning constraints represented as Gaussian processes (GPs) from locally-optimal demonstrations. Our approach uses the Karush-Kuhn-Tucker (KKT) optimality conditions to determine where on the demonstrations the constraint is tight, and a scaling of the constraint gradient at those states. We then train a GP representation of the constraint which is consistent with and which generalizes this information. We further show that the GP uncertainty can be used within a kinodynamic RRT to plan probabilistically-safe trajectories, and that we can exploit the GP structure within the planner to exactly achieve a specified safety probability. We demonstrate our method can learn complex, nonlinear constraints demonstrated on a 5D nonholonomic car, a 12D quadrotor, and a 3-link planar arm, all while requiring minimal prior information on the constraint. Our results suggest the learned GP constraint is accurate, outperforming previous constraint learning methods that require more a priori knowledge.

Model Error Propagation via Learned Contraction Metrics for Safe Feedback Motion Planning of Unknown Systems

We present a method for contraction-based feedback motion planning of locally incrementally exponentially stabilizable systems with unknown dynamics that provides probabilistic safety and reachability guarantees. Given a dynamics dataset, our method learns a deep control-affine approximation of the dynamics. To find a trusted domain where this model can be used for planning, we obtain an estimate of the Lipschitz constant of the model error, which is valid with a given probability, in a region around the training data, providing a local, spatially-varying model error bound. We derive a trajectory tracking error bound for a contraction-based controller that is subjected to this model error, and then learn a controller that optimizes this tracking bound. With a given probability, we verify the correctness of the controller and tracking error bound in the trusted domain. We then use the trajectory error bound together with the trusted domain to guide a sampling-based planner to return trajectories that can be robustly tracked in execution. We show results on a 4D car, a 6D quadrotor, and a 22D deformable object manipulation task, showing our method plans safely with learned models of high-dimensional underactuated systems, while baselines that plan without considering the tracking error bound or the trusted domain can fail to stabilize the system and become unsafe.

Uncertainty-Aware Constraint Learning for Adaptive Safe Motion Planning from Demonstrations

We present a method for learning to satisfy uncertain constraints from demonstrations. Our method uses robust optimization to obtain a belief over the potentially infinite set of possible constraints consistent with the demonstrations, and then uses this belief to plan trajectories that trade off performance with satisfying the possible constraints. We use these trajectories in a closed-loop policy that executes and replans using belief updates, which incorporate data gathered during execution. We derive guarantees on the accuracy of our constraint belief and probabilistic guarantees on plan safety. We present results on a 7-DOF arm and 12D quadrotor, showing our method can learn to satisfy high-dimensional (up to 30D) uncertain constraints, and outperforms baselines in safety and efficiency.

Planning with Learned Dynamics: Guaranteed Safety and Reachability via Lipschitz Constants

We present an approach for feedback motion planning of systems with unknown dynamics which provides guarantees on safety, reachability, and stability about the goal. Given a learned control-affine approximation of the true dynamics, we estimate the Lipschitz constant of the difference between the true and learned dynamics to determine a trusted domain for our learned model. Provided the system has at least as many controls as states, we further derive the conditions under which a one-step feedback law exists. This allows fora small bound on the tracking error when the trajectory is executed on the real system. Our method imposes a check for the existence of the feedback law as constraints in a sampling-based planner, which returns a feedback policy ensuring that under the true dynamics, the goal is reachable, the path is safe in execution, and the closed-loop system is invariant in a small set about the goal. We demonstrate our approach by planning using learned models of a 6D quadrotor and a 7DOF Kuka arm.We show that a baseline which plans using the same learned dynamics without considering the error bound or the existence of the feedback law can fail to stabilize around the plan and become unsafe.