Lyapunov-stable Neural Control for State and Output Feedback: A Novel Formulation for Efficient Synthesis and Verification

Learning-based neural network (NN) control policies have shown impressive empirical performance in a wide range of tasks in robotics and control. However, formal (Lyapunov) stability guarantees over the region-of-attraction (ROA) for NN controllers with nonlinear dynamical systems are challenging to obtain, and most existing approaches rely on expensive solvers such as sums-of-squares (SOS), mixed-integer programming (MIP), or satisfiability modulo theories (SMT). In this paper, we demonstrate a new framework for learning NN controllers together with Lyapunov certificates using fast empirical falsification and strategic regularizations. We propose a novel formulation that defines a larger verifiable region-of-attraction (ROA) than shown in the literature, and refines the conventional restrictive constraints on Lyapunov derivatives to focus only on certifiable ROAs. The Lyapunov condition is rigorously verified post-hoc using branch-and-bound with scalable linear bound propagation-based NN verification techniques. The approach is efficient and flexible, and the full training and verification procedure is accelerated on GPUs without relying on expensive solvers for SOS, MIP, nor SMT. The flexibility and efficiency of our framework allow us to demonstrate Lyapunov-stable output feedback control with synthesized NN-based controllers and NN-based observers with formal stability guarantees, for the first time in literature. Source code at https://github.com/Verified-Intelligence/Lyapunov_Stable_NN_Controllers.

Fighting Uncertainty with Gradients: Offline Reinforcement Learning via Diffusion Score Matching

Offline optimization paradigms such as offline Reinforcement Learning (RL) or Imitation Learning (IL) allow policy search algorithms to make use of offline data, but require careful incorporation of uncertainty in order to circumvent the challenges of distribution shift. Gradient-based policy search methods are a promising direction due to their effectiveness in high dimensions; however, we require a more careful consideration of how these methods interplay with uncertainty estimation. We claim that in order for an uncertainty metric to be amenable for gradient-based optimization, it must be (i) stably convergent to data when uncertainty is minimized with gradients, and (ii) not prone to underestimation of true uncertainty. We investigate smoothed distance to data as a metric, and show that it not only stably converges to data, but also allows us to analyze model bias with Lipschitz constants. Moreover, we establish an equivalence between smoothed distance to data and data likelihood, which allows us to use score-matching techniques to learn gradients of distance to data. Importantly, we show that offline model-based policy search problems that maximize data likelihood do not require values of likelihood; but rather only the gradient of the log likelihood (the score function). Using this insight, we propose Score-Guided Planning (SGP), a planning algorithm for offline RL that utilizes score-matching to enable first-order planning in high-dimensional problems, where zeroth-order methods were unable to scale, and ensembles were unable to overcome local minima. Website: https://sites.google.com/view/score-guided-planning/home

Suboptimal Controller Synthesis for Cart-Poles and Quadrotors via Sums-of-Squares

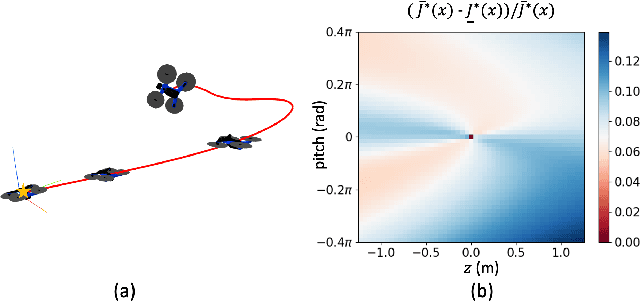
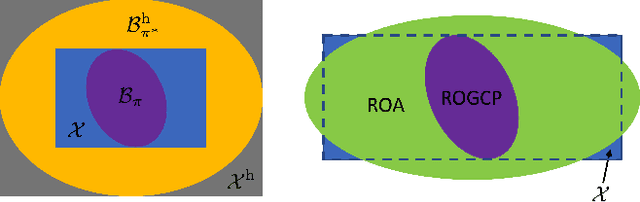
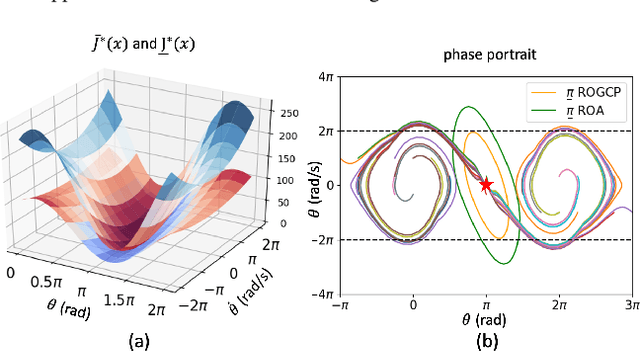
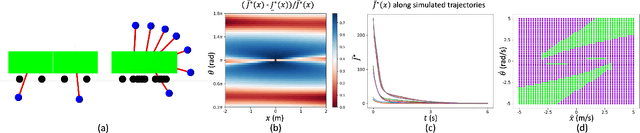
Sums-of-squares (SOS) optimization is a promising tool to synthesize certifiable controllers, but most examples to date have been limited to relatively simple systems. Here we demonstrate that SOS can synthesize controllers with bounded suboptimal performance for various underactuated robotic systems by finding good approximations of the value function. We summarize a unified SOS framework to synthesize both under- and over- approximations of the value function for continuous-time, control-affine systems, use these approximations to generate suboptimal controllers, and perform regional analysis on the closed-loop system driven by these controllers. We then extend the formulation to handle hybrid systems with contacts. We demonstrate that our method can generate tight under- and over- approximations of the value function with low-degree polynomials, which are used to provide stabilizing controllers for continuous-time systems including the inverted pendulum, the cart-pole, and the 3D quadrotor as well as a hybrid system, the planar pusher. To the best of our knowledge, this is the first time that a SOS-based time-invariant controller can swing up and stabilize a cart-pole, and push the planar slider to the desired pose.

Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models

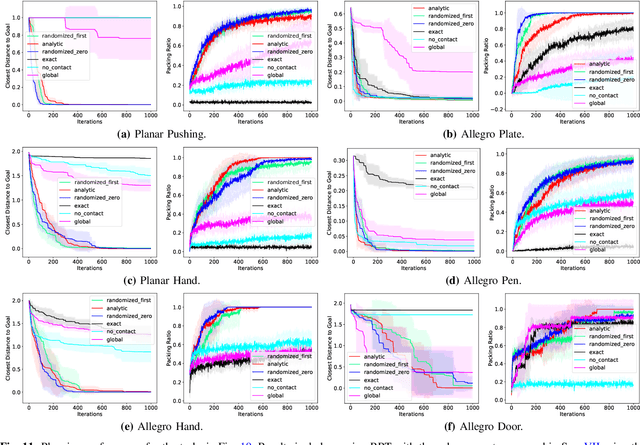
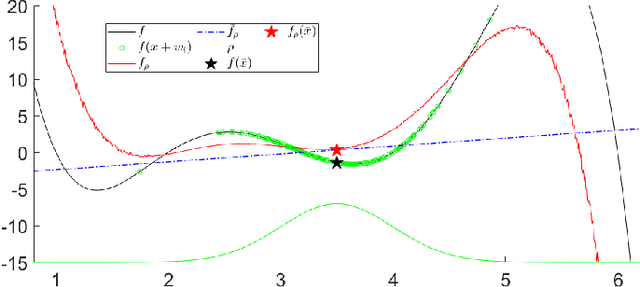
The empirical success of Reinforcement Learning (RL) in the setting of contact-rich manipulation leaves much to be understood from a model-based perspective, where the key difficulties are often attributed to (i) the explosion of contact modes, (ii) stiff, non-smooth contact dynamics and the resulting exploding / discontinuous gradients, and (iii) the non-convexity of the planning problem. The stochastic nature of RL addresses (i) and (ii) by effectively sampling and averaging the contact modes. On the other hand, model-based methods have tackled the same challenges by smoothing contact dynamics analytically. Our first contribution is to establish the theoretical equivalence of the two methods for simple systems, and provide qualitative and empirical equivalence on a number of complex examples. In order to further alleviate (ii), our second contribution is a convex, differentiable and quasi-dynamic formulation of contact dynamics, which is amenable to both smoothing schemes, and has proven through experiments to be highly effective for contact-rich planning. Our final contribution resolves (iii), where we show that classical sampling-based motion planning algorithms can be effective in global planning when contact modes are abstracted via smoothing. Applying our method on a collection of challenging contact-rich manipulation tasks, we demonstrate that efficient model-based motion planning can achieve results comparable to RL with dramatically less computation. Video: https://youtu.be/12Ew4xC-VwA

Lyapunov-stable neural-network control

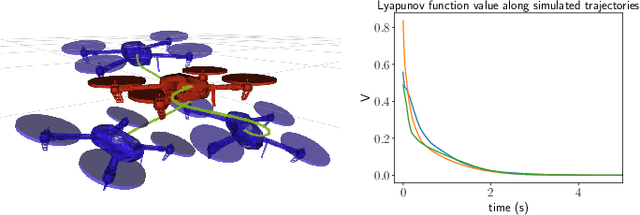
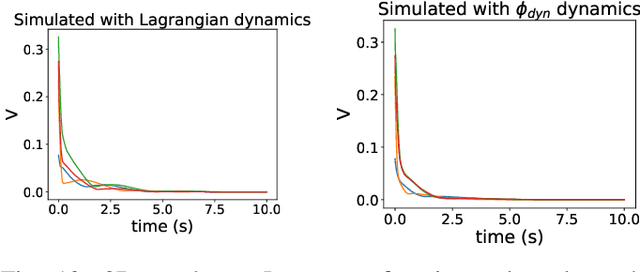
Deep learning has had a far reaching impact in robotics. Specifically, deep reinforcement learning algorithms have been highly effective in synthesizing neural-network controllers for a wide range of tasks. However, despite this empirical success, these controllers still lack theoretical guarantees on their performance, such as Lyapunov stability (i.e., all trajectories of the closed-loop system are guaranteed to converge to a goal state under the control policy). This is in stark contrast to traditional model-based controller design, where principled approaches (like LQR) can synthesize stable controllers with provable guarantees. To address this gap, we propose a generic method to synthesize a Lyapunov-stable neural-network controller, together with a neural-network Lyapunov function to simultaneously certify its stability. Our approach formulates the Lyapunov condition verification as a mixed-integer linear program (MIP). Our MIP verifier either certifies the Lyapunov condition, or generates counter examples that can help improve the candidate controller and the Lyapunov function. We also present an optimization program to compute an inner approximation of the region of attraction for the closed-loop system. We apply our approach to robots including an inverted pendulum, a 2D and a 3D quadrotor, and showcase that our neural-network controller outperforms a baseline LQR controller. The code is open sourced at \url{https://github.com/StanfordASL/neural-network-lyapunov}.