Lyapunov-stable neural-network control

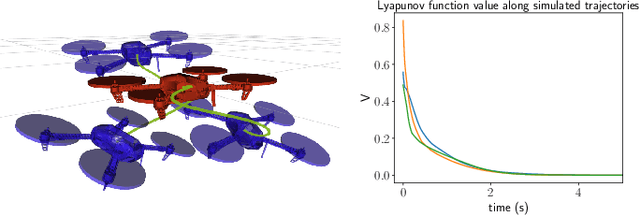
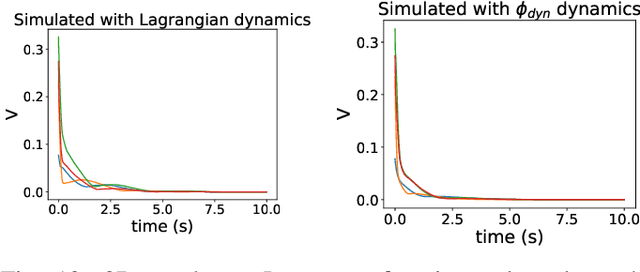
Deep learning has had a far reaching impact in robotics. Specifically, deep reinforcement learning algorithms have been highly effective in synthesizing neural-network controllers for a wide range of tasks. However, despite this empirical success, these controllers still lack theoretical guarantees on their performance, such as Lyapunov stability (i.e., all trajectories of the closed-loop system are guaranteed to converge to a goal state under the control policy). This is in stark contrast to traditional model-based controller design, where principled approaches (like LQR) can synthesize stable controllers with provable guarantees. To address this gap, we propose a generic method to synthesize a Lyapunov-stable neural-network controller, together with a neural-network Lyapunov function to simultaneously certify its stability. Our approach formulates the Lyapunov condition verification as a mixed-integer linear program (MIP). Our MIP verifier either certifies the Lyapunov condition, or generates counter examples that can help improve the candidate controller and the Lyapunov function. We also present an optimization program to compute an inner approximation of the region of attraction for the closed-loop system. We apply our approach to robots including an inverted pendulum, a 2D and a 3D quadrotor, and showcase that our neural-network controller outperforms a baseline LQR controller. The code is open sourced at \url{https://github.com/StanfordASL/neural-network-lyapunov}.

Vision-based Autonomous Disinfection of High Touch Surfaces in Indoor Environments

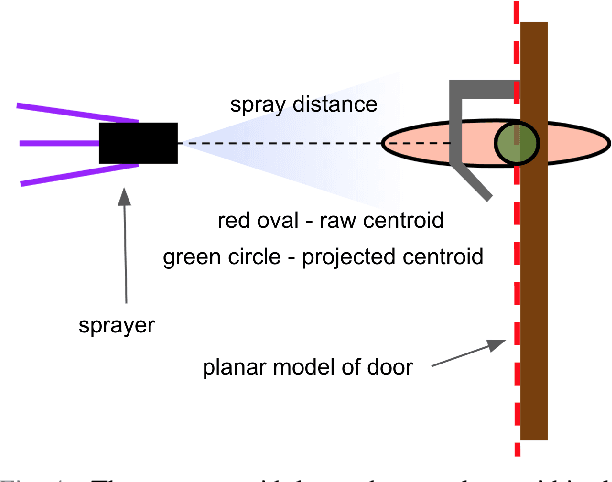
Autonomous systems have played an important role in response to the Covid-19 pandemic. Notably, there have been multiple attempts to leverage Unmanned Aerial Vehicles (UAVs) to disinfect surfaces. Although recent research suggests that surface transmission has a minimal impact in the spread of Covid-19, surfaces do play a significant role in the transmission of many other viruses. Employing UAVs for mass spray disinfection offers several potential advantages including high throughput application of disinfectant, large scale deployment, and the minimization of health risks to sanitation workers. Despite these potential benefits and preliminary usage of UAVs for disinfection, there has been little research into their design and effectiveness. In this work we present an autonomous UAV capable of effectively disinfecting surfaces. We identify relevant parameters such as disinfectant concentration, amount, and application distance required of the UAV to sterilize high touch surfaces such as door handles. Finally, we develop a robotic system that enables the fully autonomous disinfection of door handles in an unstructured, previously unknown environment. To our knowledge, this is the smallest untethered UAV ever built with both full autonomy and spraying capabilities, allowing it to operate in confined indoor settings, and the first autonomous UAV to specifically target high touch surfaces on an individual basis with spray disinfectant, resulting in more efficient use of disinfectant.

Bilevel Optimization for Planning through Contact: A Semidirect Method

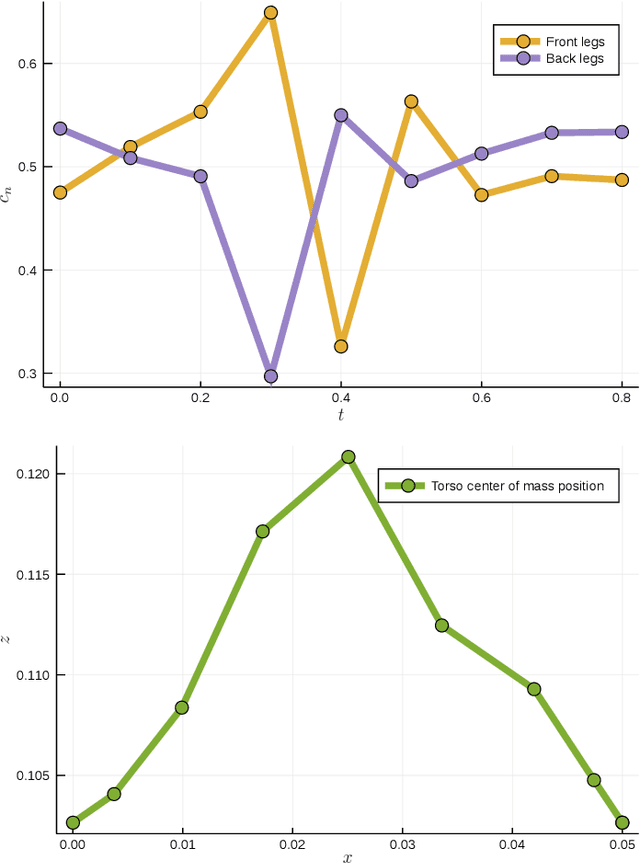
Many robotics applications, from object manipulation to locomotion, require planning methods that are capable of handling the dynamics of contact. Trajectory optimization has been shown to be a viable approach that can be made to support contact dynamics. However, the current state-of-the art methods remain slow and are often difficult to get to converge. In this work, we leverage recent advances in bilevel optimization to design an algorithm capable of efficiently generating trajectories that involve making and breaking contact. We demonstrate our method's efficiency by outperforming an alternative state-of-the-art method on a benchmark problem. We moreover demonstrate the method's ability to design a simple periodic gait for a quadruped with 15 degrees of freedom and four contact points.

A Differentiable Augmented Lagrangian Method for Bilevel Nonlinear Optimization

Many problems in modern robotics can be addressed by modeling them as bilevel optimization problems. In this work, we leverage augmented Lagrangian methods and recent advances in automatic differentiation to develop a general-purpose nonlinear optimization solver that is well suited to bilevel optimization. We then demonstrate the validity and scalability of our algorithm with two representative robotic problems, namely robust control and parameter estimation for a system involving contact. We stress the general nature of the algorithm and its potential relevance to many other problems in robotics.

Reach-Avoid Problems via Sum-of-Squares Optimization and Dynamic Programming

Reach-avoid problems involve driving a system to a set of desirable configurations while keeping it away from undesirable ones. Providing mathematical guarantees for such scenarios is challenging but have numerous potential practical applications. Due to the challenges, analysis of reach-avoid problems involves making trade-offs between generality of system dynamics, generality of problem setups, optimality of solutions, and computational complexity. In this paper, we combine sum-of-squares optimization and dynamic programming to address the reach-avoid problem, and provide a conservative solution that maintains reaching and avoidance guarantees. Our method is applicable to polynomial system dynamics and to general problem setups, and is more computationally scalable than previous related methods. Through a numerical example involving two single integrators, we validate our proposed theory and compare our method to Hamilton-Jacobi reachability. Having validated our theory, we demonstrate the computational scalability of our method by computing the reach-avoid set of a system involving two kinematic cars.

Perception-Aware Motion Planning via Multiobjective Search on GPUs

In this paper we describe a framework towards computing well-localized, robust motion plans through the perception-aware motion planning problem, whereby we seek a low-cost motion plan subject to a separate constraint on perception localization quality. To solve this problem we introduce the Multiobjective Perception-Aware Planning (MPAP) algorithm which explores the state space via a multiobjective search, considering both cost and a perception heuristic. This framework can accommodate a large range of heuristics, allowing those that capture the history dependence of localization drift and represent complex modern perception methods. We present two such heuristics, one derived from a simplified model of robot perception and a second learned from ground-truth sensor error, which we show to be capable of predicting the performance of a state-of-the-art perception system. The solution trajectory from this heuristic-based search is then certified via Monte Carlo methods to be well-localized and robust. The additional computational burden of perception-aware planning is offset by GPU massive parallelization. Through numerical experiments the algorithm is shown to find well-localized, robust solutions in about a second. Finally, we demonstrate MPAP on a quadrotor flying perception-aware and perception-agnostic plans using Google Tango for localization, finding the quadrotor safely executes the perception-aware plan every time, while crashing in over 20% of the perception-agnostic runs due to loss of localization.