Diffusion Policy Policy Optimization

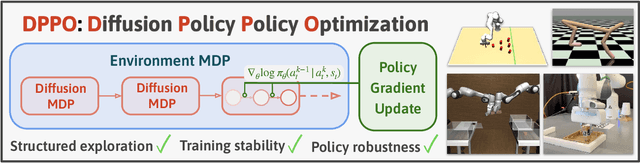
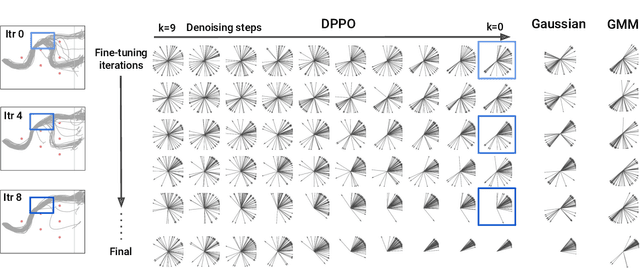
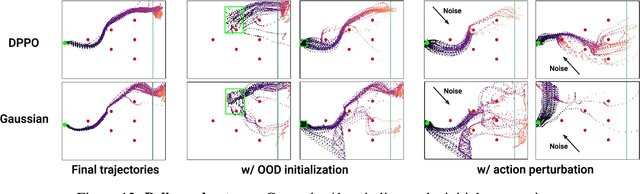
We introduce Diffusion Policy Policy Optimization, DPPO, an algorithmic framework including best practices for fine-tuning diffusion-based policies (e.g. Diffusion Policy) in continuous control and robot learning tasks using the policy gradient (PG) method from reinforcement learning (RL). PG methods are ubiquitous in training RL policies with other policy parameterizations; nevertheless, they had been conjectured to be less efficient for diffusion-based policies. Surprisingly, we show that DPPO achieves the strongest overall performance and efficiency for fine-tuning in common benchmarks compared to other RL methods for diffusion-based policies and also compared to PG fine-tuning of other policy parameterizations. Through experimental investigation, we find that DPPO takes advantage of unique synergies between RL fine-tuning and the diffusion parameterization, leading to structured and on-manifold exploration, stable training, and strong policy robustness. We further demonstrate the strengths of DPPO in a range of realistic settings, including simulated robotic tasks with pixel observations, and via zero-shot deployment of simulation-trained policies on robot hardware in a long-horizon, multi-stage manipulation task. Website with code: diffusion-ppo.github.io

Verification and Synthesis of Compatible Control Lyapunov and Control Barrier Functions

Safety and stability are essential properties of control systems. Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs) have been proposed to ensure safety and stability respectively. However, previous approaches typically verify and synthesize the CBFs and CLFs separately, satisfying their respective constraints, without proving that the CBFs and CLFs are compatible with each other, namely at every state, there exists control actions that satisfy both the CBF and CLF constraints simultaneously. There exists some recent works that synthesized compatible CLF and CBF, but relying on nominal polynomial or rational controllers, which is just a sufficient but not necessary condition for compatibility. In this work, we investigate verification and synthesis of compatible CBF and CLF independent from any nominal controllers. We derive exact necessary and sufficient conditions for compatibility, and further formulate Sum-Of-Squares program for the compatibility verification. Based on our verification framework, we also design an alternating nominal-controller-free synthesis method. We evaluate our method in a linear toy, a non-linear toy, and a power converter example.

Lyapunov-stable Neural Control for State and Output Feedback: A Novel Formulation for Efficient Synthesis and Verification

Learning-based neural network (NN) control policies have shown impressive empirical performance in a wide range of tasks in robotics and control. However, formal (Lyapunov) stability guarantees over the region-of-attraction (ROA) for NN controllers with nonlinear dynamical systems are challenging to obtain, and most existing approaches rely on expensive solvers such as sums-of-squares (SOS), mixed-integer programming (MIP), or satisfiability modulo theories (SMT). In this paper, we demonstrate a new framework for learning NN controllers together with Lyapunov certificates using fast empirical falsification and strategic regularizations. We propose a novel formulation that defines a larger verifiable region-of-attraction (ROA) than shown in the literature, and refines the conventional restrictive constraints on Lyapunov derivatives to focus only on certifiable ROAs. The Lyapunov condition is rigorously verified post-hoc using branch-and-bound with scalable linear bound propagation-based NN verification techniques. The approach is efficient and flexible, and the full training and verification procedure is accelerated on GPUs without relying on expensive solvers for SOS, MIP, nor SMT. The flexibility and efficiency of our framework allow us to demonstrate Lyapunov-stable output feedback control with synthesized NN-based controllers and NN-based observers with formal stability guarantees, for the first time in literature. Source code at https://github.com/Verified-Intelligence/Lyapunov_Stable_NN_Controllers.

Fighting Uncertainty with Gradients: Offline Reinforcement Learning via Diffusion Score Matching

Offline optimization paradigms such as offline Reinforcement Learning (RL) or Imitation Learning (IL) allow policy search algorithms to make use of offline data, but require careful incorporation of uncertainty in order to circumvent the challenges of distribution shift. Gradient-based policy search methods are a promising direction due to their effectiveness in high dimensions; however, we require a more careful consideration of how these methods interplay with uncertainty estimation. We claim that in order for an uncertainty metric to be amenable for gradient-based optimization, it must be (i) stably convergent to data when uncertainty is minimized with gradients, and (ii) not prone to underestimation of true uncertainty. We investigate smoothed distance to data as a metric, and show that it not only stably converges to data, but also allows us to analyze model bias with Lipschitz constants. Moreover, we establish an equivalence between smoothed distance to data and data likelihood, which allows us to use score-matching techniques to learn gradients of distance to data. Importantly, we show that offline model-based policy search problems that maximize data likelihood do not require values of likelihood; but rather only the gradient of the log likelihood (the score function). Using this insight, we propose Score-Guided Planning (SGP), a planning algorithm for offline RL that utilizes score-matching to enable first-order planning in high-dimensional problems, where zeroth-order methods were unable to scale, and ensembles were unable to overcome local minima. Website: https://sites.google.com/view/score-guided-planning/home

Suboptimal Controller Synthesis for Cart-Poles and Quadrotors via Sums-of-Squares

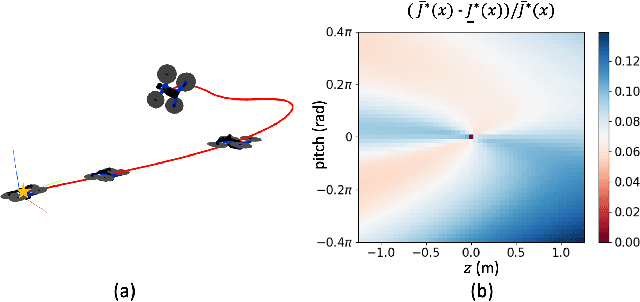
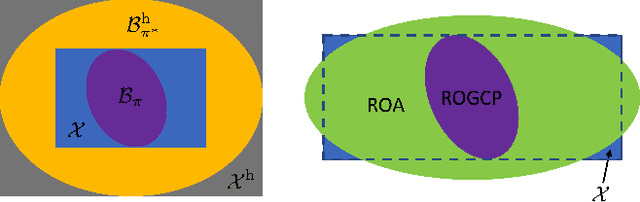
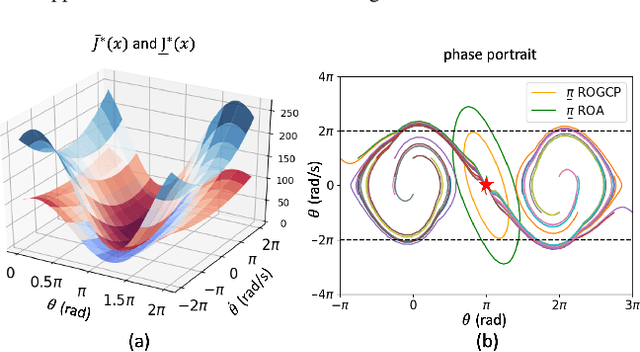
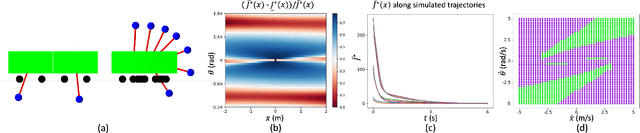
Sums-of-squares (SOS) optimization is a promising tool to synthesize certifiable controllers, but most examples to date have been limited to relatively simple systems. Here we demonstrate that SOS can synthesize controllers with bounded suboptimal performance for various underactuated robotic systems by finding good approximations of the value function. We summarize a unified SOS framework to synthesize both under- and over- approximations of the value function for continuous-time, control-affine systems, use these approximations to generate suboptimal controllers, and perform regional analysis on the closed-loop system driven by these controllers. We then extend the formulation to handle hybrid systems with contacts. We demonstrate that our method can generate tight under- and over- approximations of the value function with low-degree polynomials, which are used to provide stabilizing controllers for continuous-time systems including the inverted pendulum, the cart-pole, and the 3D quadrotor as well as a hybrid system, the planar pusher. To the best of our knowledge, this is the first time that a SOS-based time-invariant controller can swing up and stabilize a cart-pole, and push the planar slider to the desired pose.

Certified Polyhedral Decompositions of Collision-Free Configuration Space

Understanding the geometry of collision-free configuration space (C-free) in the presence of task-space obstacles is an essential ingredient for collision-free motion planning. While it is possible to check for collisions at a point using standard algorithms, to date no practical method exists for computing C-free regions with rigorous certificates due to the complexity of mapping task-space obstacles through the kinematics. In this work, we present the first to our knowledge rigorous method for approximately decomposing a rational parametrization of C-free into certified polyhedral regions. Our method, called C-IRIS (C-space Iterative Regional Inflation by Semidefinite programming), generates large, convex polytopes in a rational parameterization of the configuration space which are rigorously certified to be collision-free. Such regions have been shown to be useful for both optimization-based and randomized motion planning. Based on convex optimization, our method works in arbitrary dimensions, only makes assumptions about the convexity of the obstacles in the task space, and is fast enough to scale to realistic problems in manipulation. We demonstrate our algorithm's ability to fill a non-trivial amount of collision-free C-space in several 2-DOF examples where the C-space can be visualized, as well as the scalability of our algorithm on a 7-DOF KUKA iiwa, a 6-DOF UR3e and 12-DOF bimanual manipulators. An implementation of our algorithm is open-sourced in Drake. We furthermore provide examples of our algorithm in interactive Python notebooks.

AdaptSim: Task-Driven Simulation Adaptation for Sim-to-Real Transfer

Simulation parameter settings such as contact models and object geometry approximations are critical to training robust robotic policies capable of transferring from simulation to real-world deployment. Previous approaches typically handcraft distributions over such parameters (domain randomization), or identify parameters that best match the dynamics of the real environment (system identification). However, there is often an irreducible gap between simulation and reality: attempting to match the dynamics between simulation and reality across all states and tasks may be infeasible and may not lead to policies that perform well in reality for a specific task. Addressing this issue, we propose AdaptSim, a new task-driven adaptation framework for sim-to-real transfer that aims to optimize task performance in target (real) environments -- instead of matching dynamics between simulation and reality. First, we meta-learn an adaptation policy in simulation using reinforcement learning for adjusting the simulation parameter distribution based on the current policy's performance in a target environment. We then perform iterative real-world adaptation by inferring new simulation parameter distributions for policy training, using a small amount of real data. We perform experiments in three robotic tasks: (1) swing-up of linearized double pendulum, (2) dynamic table-top pushing of a bottle, and (3) dynamic scooping of food pieces with a spatula. Our extensive simulation and hardware experiments demonstrate AdaptSim achieving 1-3x asymptotic performance and $\sim$2x real data efficiency when adapting to different environments, compared to methods based on Sys-ID and directly training the task policy in target environments.

Convex synthesis and verification of control-Lyapunov and barrier functions with input constraints

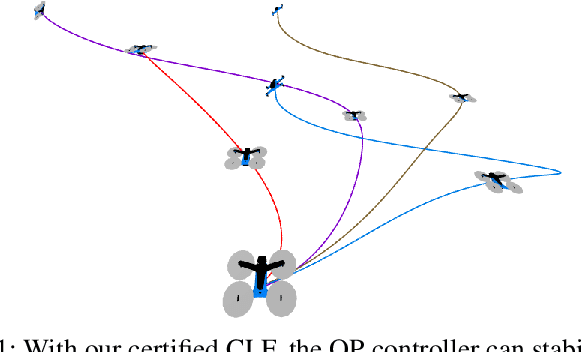
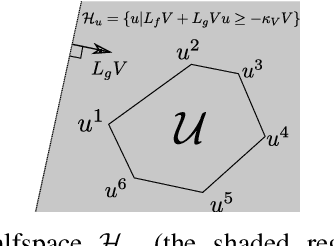
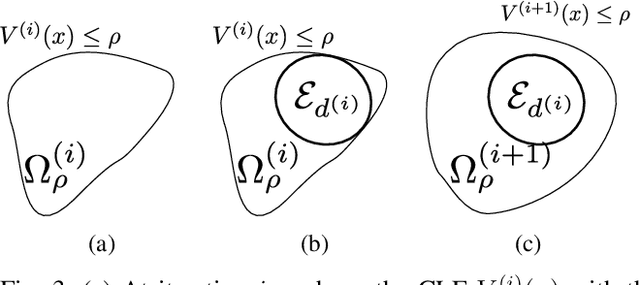
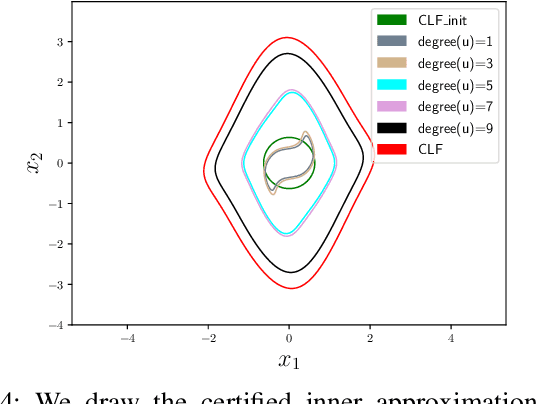
Control Lyapunov functions (CLFs) and control barrier functions (CBFs) are widely used tools for synthesizing controllers subject to stability and safety constraints. Paired with online optimization, they provide stabilizing control actions that satisfy input constraints and avoid unsafe regions of state-space. Designing CLFs and CBFs with rigorous performance guarantees is computationally challenging. To certify existence of control actions, current techniques not only design a CLF/CBF, but also a nominal controller. This can make the synthesis task more expensive, and performance estimation more conservative. In this work, we characterize polynomial CLFs/CBFs using sum-of-squares conditions, which can be directly certified using convex optimization. This yields a CLF and CBF synthesis technique that does not rely on a nominal controller. We then present algorithms for iteratively enlarging estimates of the stabilizable and safe regions. We demonstrate our algorithms on a 2D toy system, a pendulum and a quadrotor.

Finding and Optimizing Certified, Collision-Free Regions in Configuration Space for Robot Manipulators

Configuration space (C-space) has played a central role in collision-free motion planning, particularly for robot manipulators. While it is possible to check for collisions at a point using standard algorithms, to date no practical method exists for computing collision-free C-space regions with rigorous certificates due to the complexities of mapping task-space obstacles through the kinematics. In this work, we present the first to our knowledge method for generating such regions and certificates through convex optimization. Our method, called C-Iris (C-space Iterative Regional Inflation by Semidefinite programming), generates large, convex polytopes in a rational parametrization of the configuration space which are guaranteed to be collision-free. Such regions have been shown to be useful for both optimization-based and randomized motion planning. Our regions are generated by alternating between two convex optimization problems: (1) a simultaneous search for a maximal-volume ellipse inscribed in a given polytope and a certificate that the polytope is collision-free and (2) a maximal expansion of the polytope away from the ellipse which does not violate the certificate. The volume of the ellipse and size of the polytope are allowed to grow over several iterations while being collision-free by construction. Our method works in arbitrary dimensions, only makes assumptions about the convexity of the obstacles in the task space, and scales to realistic problems in manipulation. We demonstrate our algorithm's ability to fill a non-trivial amount of collision-free C-space in a 3-DOF example where the C-space can be visualized, as well as the scalability of our algorithm on a 7-DOF KUKA iiwa and a 12-DOF bimanual manipulator.

Lyapunov-stable neural-network control

Deep learning has had a far reaching impact in robotics. Specifically, deep reinforcement learning algorithms have been highly effective in synthesizing neural-network controllers for a wide range of tasks. However, despite this empirical success, these controllers still lack theoretical guarantees on their performance, such as Lyapunov stability (i.e., all trajectories of the closed-loop system are guaranteed to converge to a goal state under the control policy). This is in stark contrast to traditional model-based controller design, where principled approaches (like LQR) can synthesize stable controllers with provable guarantees. To address this gap, we propose a generic method to synthesize a Lyapunov-stable neural-network controller, together with a neural-network Lyapunov function to simultaneously certify its stability. Our approach formulates the Lyapunov condition verification as a mixed-integer linear program (MIP). Our MIP verifier either certifies the Lyapunov condition, or generates counter examples that can help improve the candidate controller and the Lyapunov function. We also present an optimization program to compute an inner approximation of the region of attraction for the closed-loop system. We apply our approach to robots including an inverted pendulum, a 2D and a 3D quadrotor, and showcase that our neural-network controller outperforms a baseline LQR controller. The code is open sourced at \url{https://github.com/StanfordASL/neural-network-lyapunov}.