Enhancing Sample Generation of Diffusion Models using Noise Level Correction

The denoising process of diffusion models can be interpreted as a projection of noisy samples onto the data manifold. Moreover, the noise level in these samples approximates their distance to the underlying manifold. Building on this insight, we propose a novel method to enhance sample generation by aligning the estimated noise level with the true distance of noisy samples to the manifold. Specifically, we introduce a noise level correction network, leveraging a pre-trained denoising network, to refine noise level estimates during the denoising process. Additionally, we extend this approach to various image restoration tasks by integrating task-specific constraints, including inpainting, deblurring, super-resolution, colorization, and compressed sensing. Experimental results demonstrate that our method significantly improves sample quality in both unconstrained and constrained generation scenarios. Notably, the proposed noise level correction framework is compatible with existing denoising schedulers (e.g., DDIM), offering additional performance improvements.

Parametric-ControlNet: Multimodal Control in Foundation Models for Precise Engineering Design Synthesis

This paper introduces a generative model designed for multimodal control over text-to-image foundation generative AI models such as Stable Diffusion, specifically tailored for engineering design synthesis. Our model proposes parametric, image, and text control modalities to enhance design precision and diversity. Firstly, it handles both partial and complete parametric inputs using a diffusion model that acts as a design autocomplete co-pilot, coupled with a parametric encoder to process the information. Secondly, the model utilizes assembly graphs to systematically assemble input component images, which are then processed through a component encoder to capture essential visual data. Thirdly, textual descriptions are integrated via CLIP encoding, ensuring a comprehensive interpretation of design intent. These diverse inputs are synthesized through a multimodal fusion technique, creating a joint embedding that acts as the input to a module inspired by ControlNet. This integration allows the model to apply robust multimodal control to foundation models, facilitating the generation of complex and precise engineering designs. This approach broadens the capabilities of AI-driven design tools and demonstrates significant advancements in precise control based on diverse data modalities for enhanced design generation.

Bridging Design Gaps: A Parametric Data Completion Approach With Graph Guided Diffusion Models

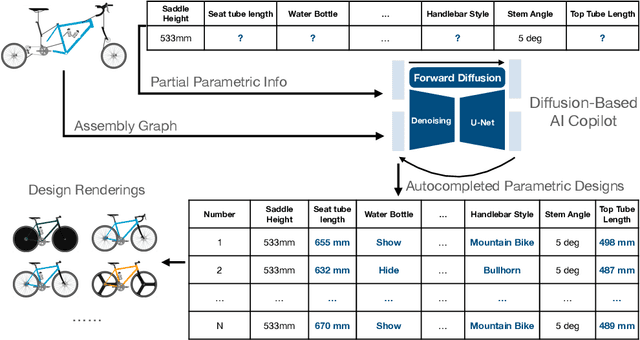
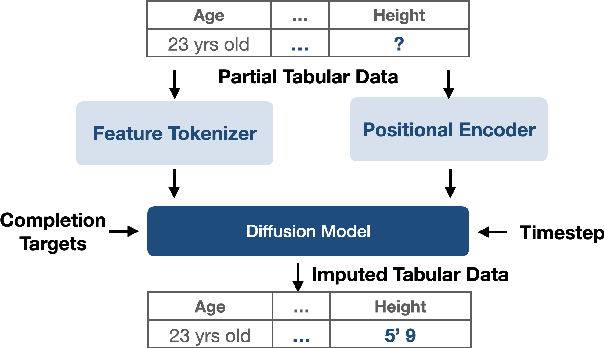
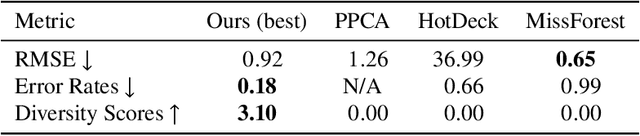
This study introduces a generative imputation model leveraging graph attention networks and tabular diffusion models for completing missing parametric data in engineering designs. This model functions as an AI design co-pilot, providing multiple design options for incomplete designs, which we demonstrate using the bicycle design CAD dataset. Through comparative evaluations, we demonstrate that our model significantly outperforms existing classical methods, such as MissForest, hotDeck, PPCA, and tabular generative method TabCSDI in both the accuracy and diversity of imputation options. Generative modeling also enables a broader exploration of design possibilities, thereby enhancing design decision-making by allowing engineers to explore a variety of design completions. The graph model combines GNNs with the structural information contained in assembly graphs, enabling the model to understand and predict the complex interdependencies between different design parameters. The graph model helps accurately capture and impute complex parametric interdependencies from an assembly graph, which is key for design problems. By learning from an existing dataset of designs, the imputation capability allows the model to act as an intelligent assistant that autocompletes CAD designs based on user-defined partial parametric design, effectively bridging the gap between ideation and realization. The proposed work provides a pathway to not only facilitate informed design decisions but also promote creative exploration in design.

Drag-guided diffusion models for vehicle image generation

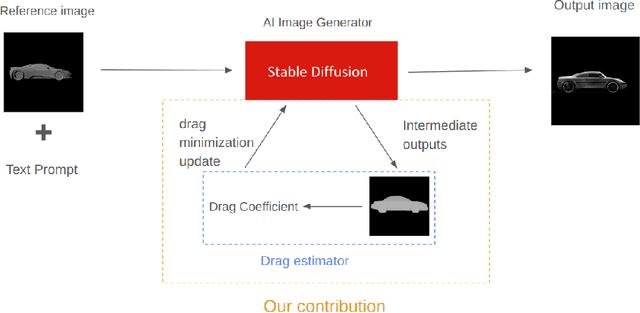
Denoising diffusion models trained at web-scale have revolutionized image generation. The application of these tools to engineering design is an intriguing possibility, but is currently limited by their inability to parse and enforce concrete engineering constraints. In this paper, we take a step towards this goal by proposing physics-based guidance, which enables optimization of a performance metric (as predicted by a surrogate model) during the generation process. As a proof-of-concept, we add drag guidance to Stable Diffusion, which allows this tool to generate images of novel vehicles while simultaneously minimizing their predicted drag coefficients.

Interpreting and Improving Diffusion Models Using the Euclidean Distance Function

Denoising is intuitively related to projection. Indeed, under the manifold hypothesis, adding random noise is approximately equivalent to orthogonal perturbation. Hence, learning to denoise is approximately learning to project. In this paper, we use this observation to reinterpret denoising diffusion models as approximate gradient descent applied to the Euclidean distance function. We then provide straight-forward convergence analysis of the DDIM sampler under simple assumptions on the projection-error of the denoiser. Finally, we propose a new sampler based on two simple modifications to DDIM using insights from our theoretical results. In as few as 5-10 function evaluations, our sampler achieves state-of-the-art FID scores on pretrained CIFAR-10 and CelebA models and can generate high quality samples on latent diffusion models.

Surrogate Modeling of Car Drag Coefficient with Depth and Normal Renderings

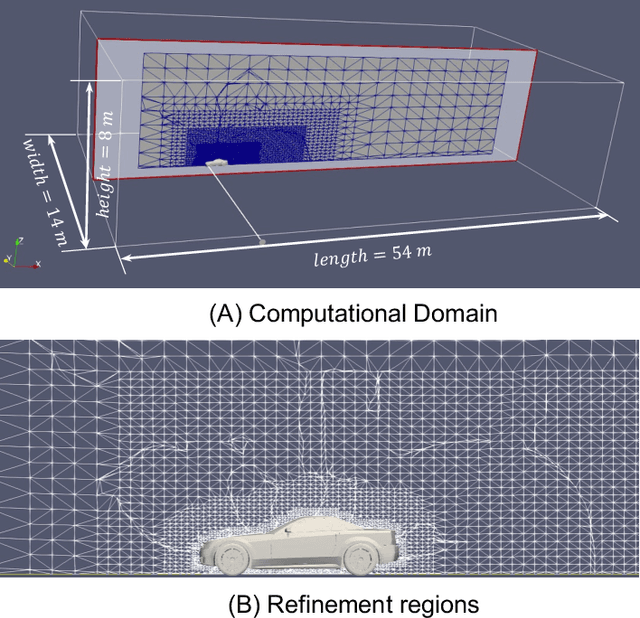
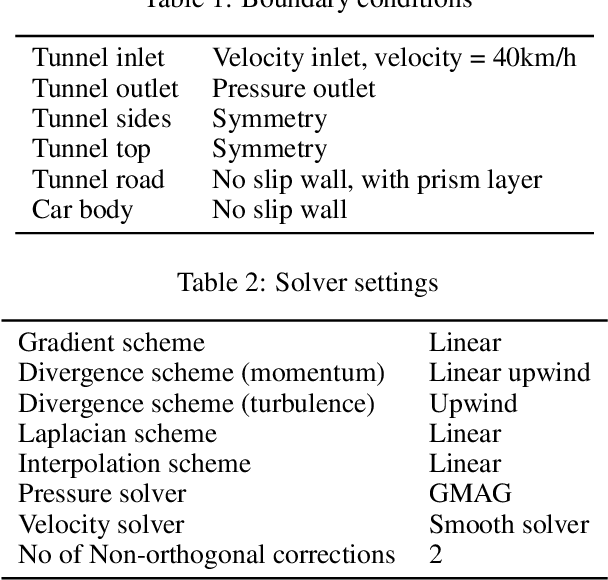
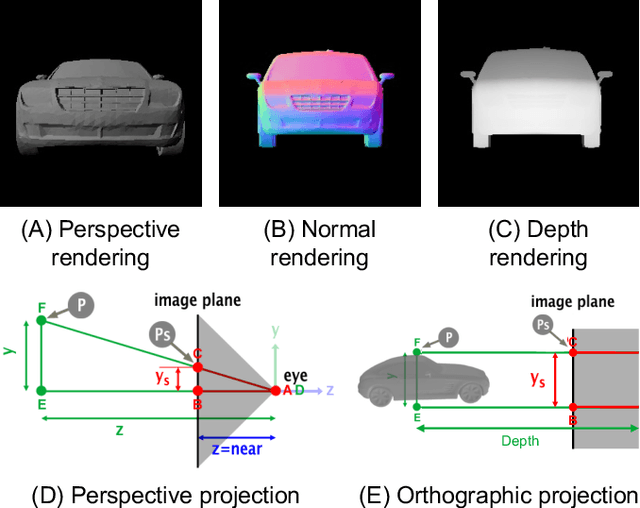
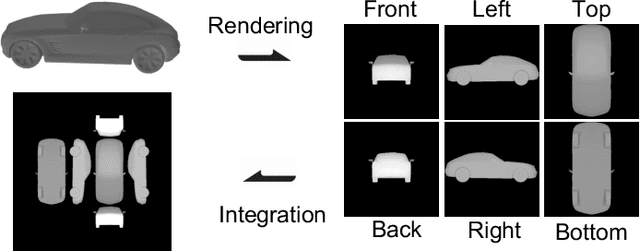
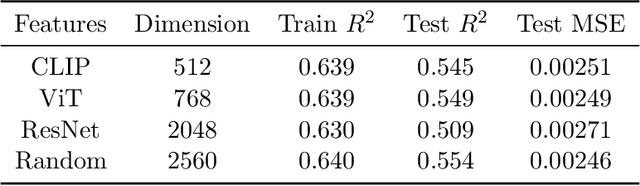
Generative AI models have made significant progress in automating the creation of 3D shapes, which has the potential to transform car design. In engineering design and optimization, evaluating engineering metrics is crucial. To make generative models performance-aware and enable them to create high-performing designs, surrogate modeling of these metrics is necessary. However, the currently used representations of three-dimensional (3D) shapes either require extensive computational resources to learn or suffer from significant information loss, which impairs their effectiveness in surrogate modeling. To address this issue, we propose a new two-dimensional (2D) representation of 3D shapes. We develop a surrogate drag model based on this representation to verify its effectiveness in predicting 3D car drag. We construct a diverse dataset of 9,070 high-quality 3D car meshes labeled by drag coefficients computed from computational fluid dynamics (CFD) simulations to train our model. Our experiments demonstrate that our model can accurately and efficiently evaluate drag coefficients with an $R^2$ value above 0.84 for various car categories. Moreover, the proposed representation method can be generalized to many other product categories beyond cars. Our model is implemented using deep neural networks, making it compatible with recent AI image generation tools (such as Stable Diffusion) and a significant step towards the automatic generation of drag-optimized car designs. We have made the dataset and code publicly available at https://decode.mit.edu/projects/dragprediction/.

Convex synthesis and verification of control-Lyapunov and barrier functions with input constraints

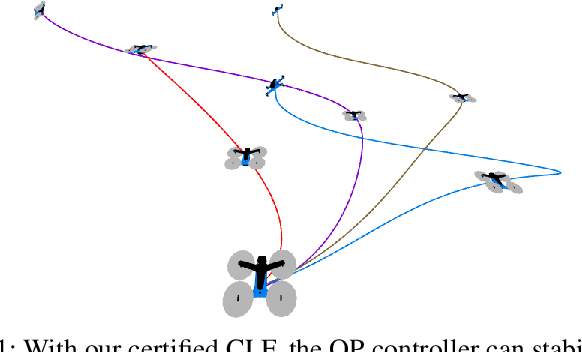
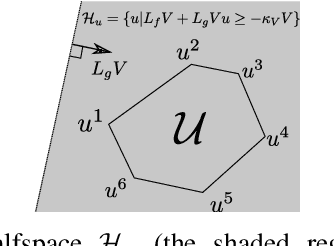
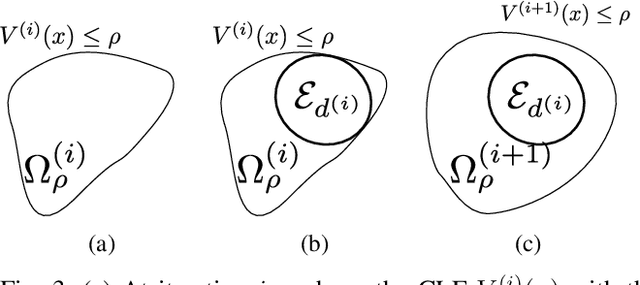
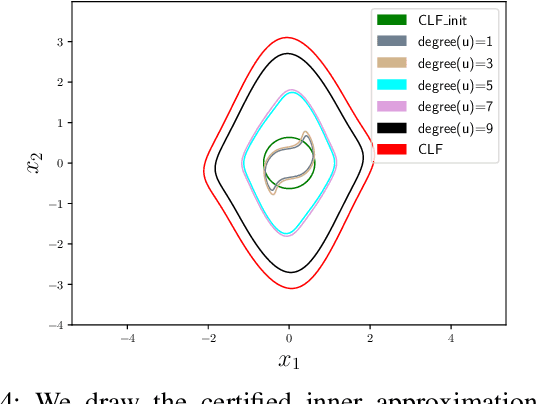
Control Lyapunov functions (CLFs) and control barrier functions (CBFs) are widely used tools for synthesizing controllers subject to stability and safety constraints. Paired with online optimization, they provide stabilizing control actions that satisfy input constraints and avoid unsafe regions of state-space. Designing CLFs and CBFs with rigorous performance guarantees is computationally challenging. To certify existence of control actions, current techniques not only design a CLF/CBF, but also a nominal controller. This can make the synthesis task more expensive, and performance estimation more conservative. In this work, we characterize polynomial CLFs/CBFs using sum-of-squares conditions, which can be directly certified using convex optimization. This yields a CLF and CBF synthesis technique that does not rely on a nominal controller. We then present algorithms for iteratively enlarging estimates of the stabilizable and safe regions. We demonstrate our algorithms on a 2D toy system, a pendulum and a quadrotor.

An Efficiently Solvable Quadratic Program for Stabilizing Dynamic Locomotion

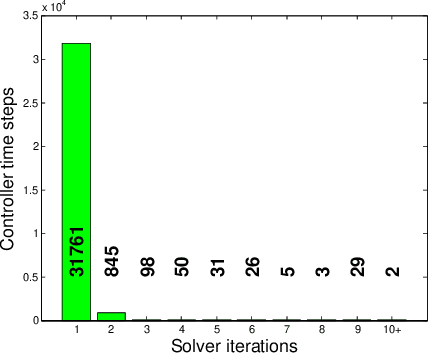
We describe a whole-body dynamic walking controller implemented as a convex quadratic program. The controller solves an optimal control problem using an approximate value function derived from a simple walking model while respecting the dynamic, input, and contact constraints of the full robot dynamics. By exploiting sparsity and temporal structure in the optimization with a custom active-set algorithm, we surpass the performance of the best available off-the-shelf solvers and achieve 1kHz control rates for a 34-DOF humanoid. We describe applications to balancing and walking tasks using the simulated Atlas robot in the DARPA Virtual Robotics Challenge.