Convex synthesis and verification of control-Lyapunov and barrier functions with input constraints
Paper and Code
Oct 02, 2022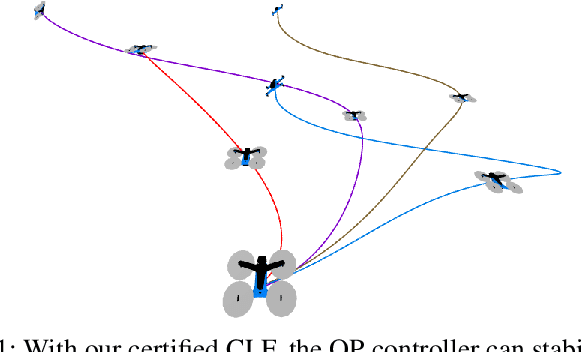
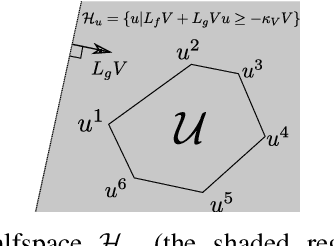
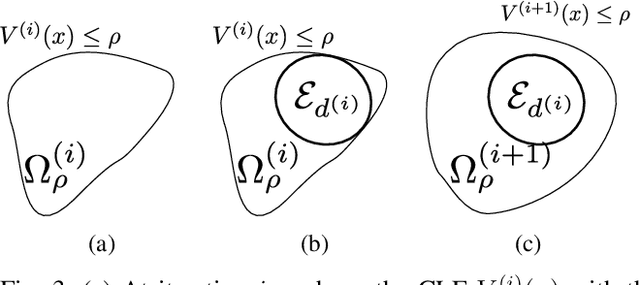
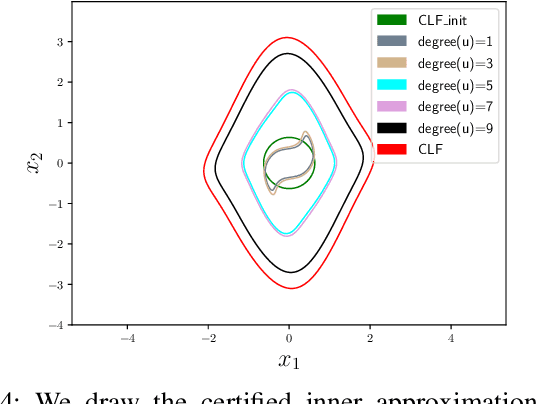
Control Lyapunov functions (CLFs) and control barrier functions (CBFs) are widely used tools for synthesizing controllers subject to stability and safety constraints. Paired with online optimization, they provide stabilizing control actions that satisfy input constraints and avoid unsafe regions of state-space. Designing CLFs and CBFs with rigorous performance guarantees is computationally challenging. To certify existence of control actions, current techniques not only design a CLF/CBF, but also a nominal controller. This can make the synthesis task more expensive, and performance estimation more conservative. In this work, we characterize polynomial CLFs/CBFs using sum-of-squares conditions, which can be directly certified using convex optimization. This yields a CLF and CBF synthesis technique that does not rely on a nominal controller. We then present algorithms for iteratively enlarging estimates of the stabilizable and safe regions. We demonstrate our algorithms on a 2D toy system, a pendulum and a quadrotor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge