Zhouxing Shi
PII-VisBench: Evaluating Personally Identifiable Information Safety in Vision Language Models Along a Continuum of Visibility
Jan 09, 2026Abstract:Vision Language Models (VLMs) are increasingly integrated into privacy-critical domains, yet existing evaluations of personally identifiable information (PII) leakage largely treat privacy as a static extraction task and ignore how a subject's online presence--the volume of their data available online--influences privacy alignment. We introduce PII-VisBench, a novel benchmark containing 4000 unique probes designed to evaluate VLM safety through the continuum of online presence. The benchmark stratifies 200 subjects into four visibility categories: high, medium, low, and zero--based on the extent and nature of their information available online. We evaluate 18 open-source VLMs (0.3B-32B) based on two key metrics: percentage of PII probing queries refused (Refusal Rate) and the fraction of non-refusal responses flagged for containing PII (Conditional PII Disclosure Rate). Across models, we observe a consistent pattern: refusals increase and PII disclosures decrease (9.10% high to 5.34% low) as subject visibility drops. We identify that models are more likely to disclose PII for high-visibility subjects, alongside substantial model-family heterogeneity and PII-type disparities. Finally, paraphrasing and jailbreak-style prompts expose attack and model-dependent failures, motivating visibility-aware safety evaluation and training interventions.
Bridging Efficiency and Safety: Formal Verification of Neural Networks with Early Exits
Dec 23, 2025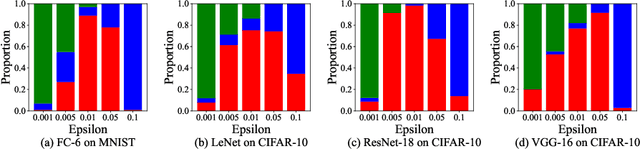
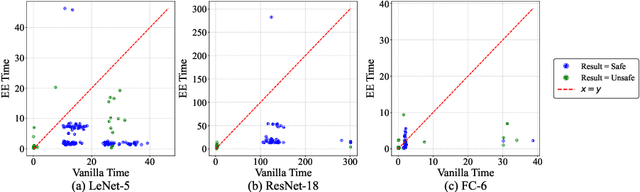


Abstract:Ensuring the safety and efficiency of AI systems is a central goal of modern research. Formal verification provides guarantees of neural network robustness, while early exits improve inference efficiency by enabling intermediate predictions. Yet verifying networks with early exits introduces new challenges due to their conditional execution paths. In this work, we define a robustness property tailored to early exit architectures and show how off-the-shelf solvers can be used to assess it. We present a baseline algorithm, enhanced with an early stopping strategy and heuristic optimizations that maintain soundness and completeness. Experiments on multiple benchmarks validate our framework's effectiveness and demonstrate the performance gains of the improved algorithm. Alongside the natural inference acceleration provided by early exits, we show that they also enhance verifiability, enabling more queries to be solved in less time compared to standard networks. Together with a robustness analysis, we show how these metrics can help users navigate the inherent trade-off between accuracy and efficiency.
Testing Neural Network Verifiers: A Soundness Benchmark with Hidden Counterexamples
Dec 04, 2024



Abstract:In recent years, many neural network (NN) verifiers have been developed to formally verify certain properties of neural networks such as robustness. Although many benchmarks have been constructed to evaluate the performance of NN verifiers, they typically lack a ground-truth for hard instances where no current verifier can verify and no counterexample can be found, which makes it difficult to check the soundness of a new verifier if it claims to verify hard instances which no other verifier can do. We propose to develop a soundness benchmark for NN verification. Our benchmark contains instances with deliberately inserted counterexamples while we also try to hide the counterexamples from regular adversarial attacks which can be used for finding counterexamples. We design a training method to produce neural networks with such hidden counterexamples. Our benchmark aims to be used for testing the soundness of NN verifiers and identifying falsely claimed verifiability when it is known that hidden counterexamples exist. We systematically construct our benchmark and generate instances across diverse model architectures, activation functions, input sizes, and perturbation radii. We demonstrate that our benchmark successfully identifies bugs in state-of-the-art NN verifiers, as well as synthetic bugs, providing a crucial step toward enhancing the reliability of testing NN verifiers. Our code is available at https://github.com/MVP-Harry/SoundnessBench and our benchmark is available at https://huggingface.co/datasets/SoundnessBench/SoundnessBench.
Certified Training with Branch-and-Bound: A Case Study on Lyapunov-stable Neural Control
Nov 27, 2024



Abstract:We study the problem of learning Lyapunov-stable neural controllers which provably satisfy the Lyapunov asymptotic stability condition within a region-of-attraction. Compared to previous works which commonly used counterexample guided training on this task, we develop a new and generally formulated certified training framework named CT-BaB, and we optimize for differentiable verified bounds, to produce verification-friendly models. In order to handle the relatively large region-of-interest, we propose a novel framework of training-time branch-and-bound to dynamically maintain a training dataset of subregions throughout training, such that the hardest subregions are iteratively split into smaller ones whose verified bounds can be computed more tightly to ease the training. We demonstrate that our new training framework can produce models which can be more efficiently verified at test time. On the largest 2D quadrotor dynamical system, verification for our model is more than 5X faster compared to the baseline, while our size of region-of-attraction is 16X larger than the baseline.
Neural Network Verification with Branch-and-Bound for General Nonlinearities
May 31, 2024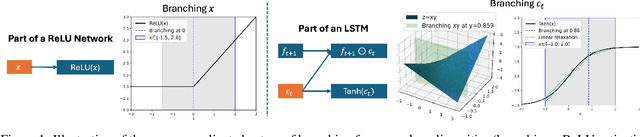

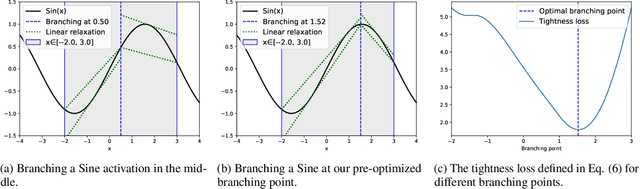
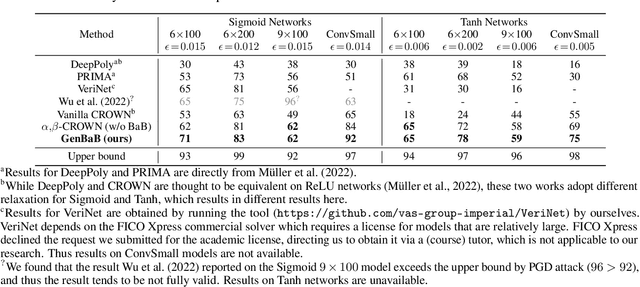
Abstract:Branch-and-bound (BaB) is among the most effective methods for neural network (NN) verification. However, existing works on BaB have mostly focused on NNs with piecewise linear activations, especially ReLU networks. In this paper, we develop a general framework, named GenBaB, to conduct BaB for general nonlinearities in general computational graphs based on linear bound propagation. To decide which neuron to branch, we design a new branching heuristic which leverages linear bounds as shortcuts to efficiently estimate the potential improvement after branching. To decide nontrivial branching points for general nonlinear functions, we propose to optimize branching points offline, which can be efficiently leveraged during verification with a lookup table. We demonstrate the effectiveness of our GenBaB on verifying a wide range of NNs, including networks with activation functions such as Sigmoid, Tanh, Sine and GeLU, as well as networks involving multi-dimensional nonlinear operations such as multiplications in LSTMs and Vision Transformers. Our framework also allows the verification of general nonlinear computation graphs and enables verification applications beyond simple neural networks, particularly for AC Optimal Power Flow (ACOPF). GenBaB is part of the latest $\alpha,\!\beta$-CROWN, the winner of the 4th International Verification of Neural Networks Competition (VNN-COMP 2023).
Lyapunov-stable Neural Control for State and Output Feedback: A Novel Formulation for Efficient Synthesis and Verification
Apr 11, 2024



Abstract:Learning-based neural network (NN) control policies have shown impressive empirical performance in a wide range of tasks in robotics and control. However, formal (Lyapunov) stability guarantees over the region-of-attraction (ROA) for NN controllers with nonlinear dynamical systems are challenging to obtain, and most existing approaches rely on expensive solvers such as sums-of-squares (SOS), mixed-integer programming (MIP), or satisfiability modulo theories (SMT). In this paper, we demonstrate a new framework for learning NN controllers together with Lyapunov certificates using fast empirical falsification and strategic regularizations. We propose a novel formulation that defines a larger verifiable region-of-attraction (ROA) than shown in the literature, and refines the conventional restrictive constraints on Lyapunov derivatives to focus only on certifiable ROAs. The Lyapunov condition is rigorously verified post-hoc using branch-and-bound with scalable linear bound propagation-based NN verification techniques. The approach is efficient and flexible, and the full training and verification procedure is accelerated on GPUs without relying on expensive solvers for SOS, MIP, nor SMT. The flexibility and efficiency of our framework allow us to demonstrate Lyapunov-stable output feedback control with synthesized NN-based controllers and NN-based observers with formal stability guarantees, for the first time in literature. Source code at https://github.com/Verified-Intelligence/Lyapunov_Stable_NN_Controllers.
Defending LLMs against Jailbreaking Attacks via Backtranslation
Feb 28, 2024Abstract:Although many large language models (LLMs) have been trained to refuse harmful requests, they are still vulnerable to jailbreaking attacks, which rewrite the original prompt to conceal its harmful intent. In this paper, we propose a new method for defending LLMs against jailbreaking attacks by ``backtranslation''. Specifically, given an initial response generated by the target LLM from an input prompt, our backtranslation prompts a language model to infer an input prompt that can lead to the response. The inferred prompt is called the backtranslated prompt which tends to reveal the actual intent of the original prompt, since it is generated based on the LLM's response and is not directly manipulated by the attacker. We then run the target LLM again on the backtranslated prompt, and we refuse the original prompt if the model refuses the backtranslated prompt. We explain that the proposed defense provides several benefits on its effectiveness and efficiency. We empirically demonstrate that our defense significantly outperforms the baselines, in the cases that are hard for the baselines, and our defense also has little impact on the generation quality for benign input prompts.
Improving the Generation Quality of Watermarked Large Language Models via Word Importance Scoring
Nov 16, 2023
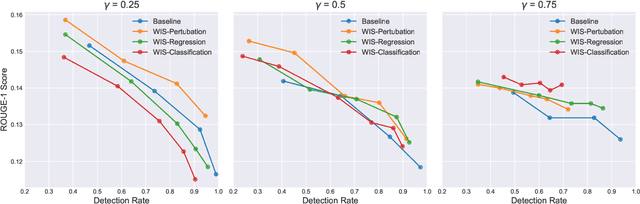
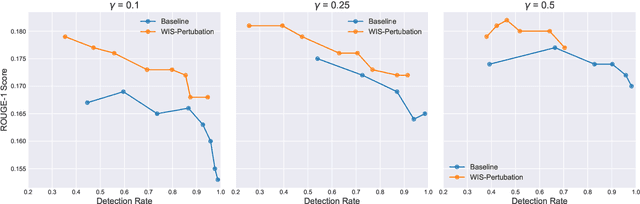
Abstract:The strong general capabilities of Large Language Models (LLMs) bring potential ethical risks if they are unrestrictedly accessible to malicious users. Token-level watermarking inserts watermarks in the generated texts by altering the token probability distributions with a private random number generator seeded by its prefix tokens. However, this watermarking algorithm alters the logits during generation, which can lead to a downgraded text quality if it chooses to promote tokens that are less relevant given the input. In this work, we propose to improve the quality of texts generated by a watermarked language model by Watermarking with Importance Scoring (WIS). At each generation step, we estimate the importance of the token to generate, and prevent it from being impacted by watermarking if it is important for the semantic correctness of the output. We further propose three methods to predict importance scoring, including a perturbation-based method and two model-based methods. Empirical experiments show that our method can generate texts with better quality with comparable level of detection rate.
Red Teaming Language Model Detectors with Language Models
May 31, 2023Abstract:The prevalence and high capacity of large language models (LLMs) present significant safety and ethical risks when malicious users exploit them for automated content generation. To prevent the potentially deceptive usage of LLMs, recent works have proposed several algorithms to detect machine-generated text. In this paper, we systematically test the reliability of the existing detectors, by designing two types of attack strategies to fool the detectors: 1) replacing words with their synonyms based on the context; 2) altering the writing style of generated text. These strategies are implemented by instructing LLMs to generate synonymous word substitutions or writing directives that modify the style without human involvement, and the LLMs leveraged in the attack can also be protected by detectors. Our research reveals that our attacks effectively compromise the performance of all tested detectors, thereby underscoring the urgent need for the development of more robust machine-generated text detection systems.
Effective Robustness against Natural Distribution Shifts for Models with Different Training Data
Feb 02, 2023Abstract:``Effective robustness'' measures the extra out-of-distribution (OOD) robustness beyond what can be predicted from the in-distribution (ID) performance. Existing effective robustness evaluations typically use a single test set such as ImageNet to evaluate ID accuracy. This becomes problematic when evaluating models trained on different data distributions, e.g., comparing models trained on ImageNet vs. zero-shot language-image pre-trained models trained on LAION. In this paper, we propose a new effective robustness evaluation metric to compare the effective robustness of models trained on different data distributions. To do this we control for the accuracy on multiple ID test sets that cover the training distributions for all the evaluated models. Our new evaluation metric provides a better estimate of the effectiveness robustness and explains the surprising effective robustness gains of zero-shot CLIP-like models exhibited when considering only one ID dataset, while the gains diminish under our evaluation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge