Neural Network Verification with Branch-and-Bound for General Nonlinearities

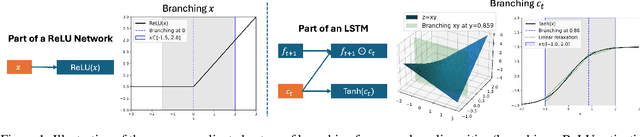
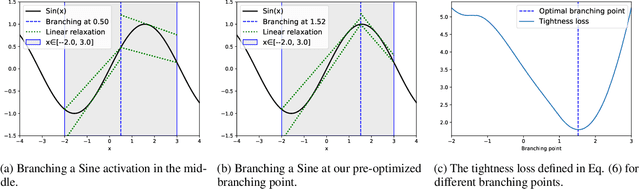
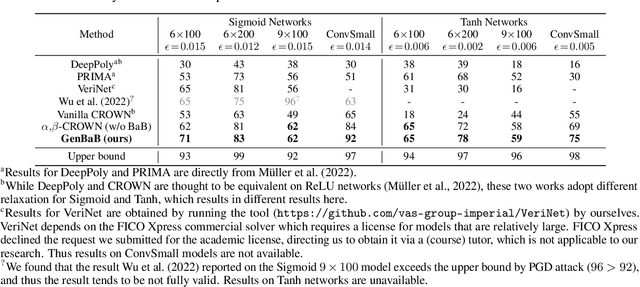
Branch-and-bound (BaB) is among the most effective methods for neural network (NN) verification. However, existing works on BaB have mostly focused on NNs with piecewise linear activations, especially ReLU networks. In this paper, we develop a general framework, named GenBaB, to conduct BaB for general nonlinearities in general computational graphs based on linear bound propagation. To decide which neuron to branch, we design a new branching heuristic which leverages linear bounds as shortcuts to efficiently estimate the potential improvement after branching. To decide nontrivial branching points for general nonlinear functions, we propose to optimize branching points offline, which can be efficiently leveraged during verification with a lookup table. We demonstrate the effectiveness of our GenBaB on verifying a wide range of NNs, including networks with activation functions such as Sigmoid, Tanh, Sine and GeLU, as well as networks involving multi-dimensional nonlinear operations such as multiplications in LSTMs and Vision Transformers. Our framework also allows the verification of general nonlinear computation graphs and enables verification applications beyond simple neural networks, particularly for AC Optimal Power Flow (ACOPF). GenBaB is part of the latest $\alpha,\!\beta$-CROWN, the winner of the 4th International Verification of Neural Networks Competition (VNN-COMP 2023).

Symmetry-Preserving Program Representations for Learning Code Semantics

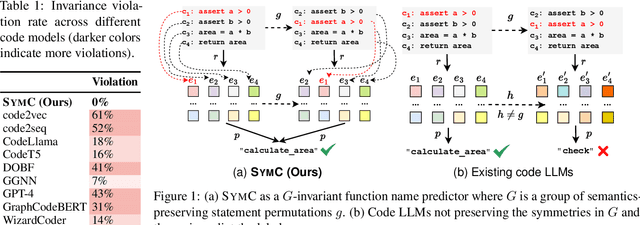
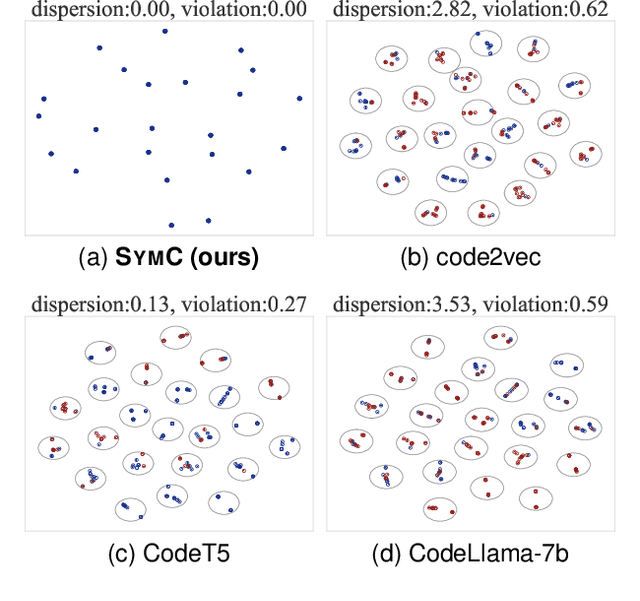
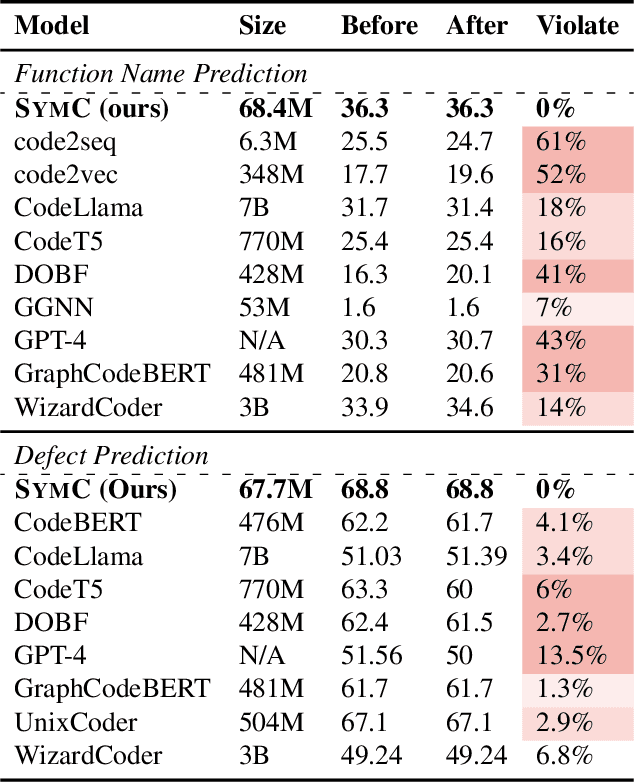
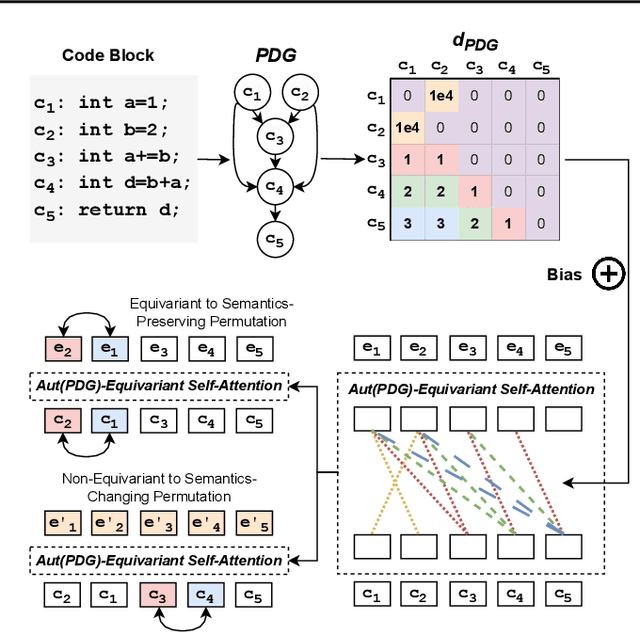
Large Language Models (LLMs) have shown promise in automated program reasoning, a crucial aspect of many security tasks. However, existing LLM architectures for code are often borrowed from other domains like natural language processing, raising concerns about their generalization and robustness to unseen code. A key generalization challenge is to incorporate the knowledge of code semantics, including control and data flow, into the LLM architectures. Drawing inspiration from examples of convolution layers exploiting translation symmetry, we explore how code symmetries can enhance LLM architectures for program analysis and modeling. We present a rigorous group-theoretic framework that formally defines code symmetries as semantics-preserving transformations and provides techniques for precisely reasoning about symmetry preservation within LLM architectures. Using this framework, we introduce a novel variant of self-attention that preserves program symmetries, demonstrating its effectiveness in generalization and robustness through detailed experimental evaluations across different binary and source code analysis tasks. Overall, our code symmetry framework offers rigorous and powerful reasoning techniques that can guide the future development of specialized LLMs for code and advance LLM-guided program reasoning tasks.