Neural Network Verification with Branch-and-Bound for General Nonlinearities
Paper and Code
May 31, 2024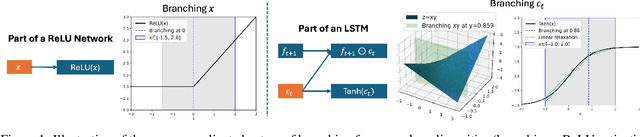

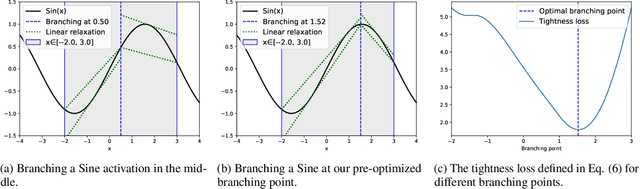
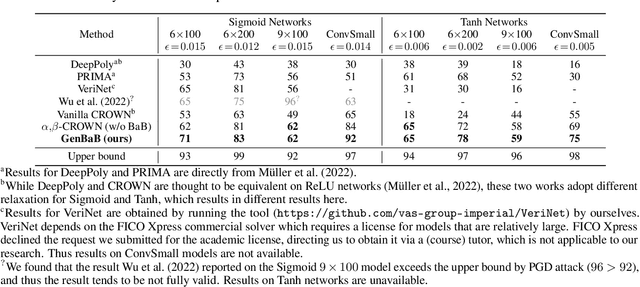
Branch-and-bound (BaB) is among the most effective methods for neural network (NN) verification. However, existing works on BaB have mostly focused on NNs with piecewise linear activations, especially ReLU networks. In this paper, we develop a general framework, named GenBaB, to conduct BaB for general nonlinearities in general computational graphs based on linear bound propagation. To decide which neuron to branch, we design a new branching heuristic which leverages linear bounds as shortcuts to efficiently estimate the potential improvement after branching. To decide nontrivial branching points for general nonlinear functions, we propose to optimize branching points offline, which can be efficiently leveraged during verification with a lookup table. We demonstrate the effectiveness of our GenBaB on verifying a wide range of NNs, including networks with activation functions such as Sigmoid, Tanh, Sine and GeLU, as well as networks involving multi-dimensional nonlinear operations such as multiplications in LSTMs and Vision Transformers. Our framework also allows the verification of general nonlinear computation graphs and enables verification applications beyond simple neural networks, particularly for AC Optimal Power Flow (ACOPF). GenBaB is part of the latest $\alpha,\!\beta$-CROWN, the winner of the 4th International Verification of Neural Networks Competition (VNN-COMP 2023).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge