On the Convergence of Certified Robust Training with Interval Bound Propagation
Paper and Code
Mar 16, 2022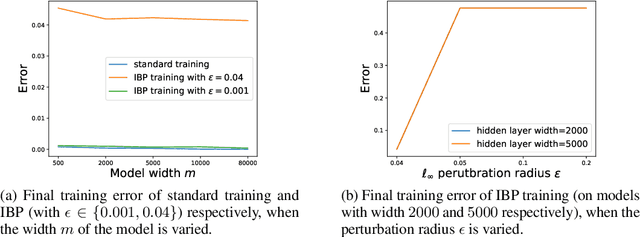
Interval Bound Propagation (IBP) is so far the base of state-of-the-art methods for training neural networks with certifiable robustness guarantees when potential adversarial perturbations present, while the convergence of IBP training remains unknown in existing literature. In this paper, we present a theoretical analysis on the convergence of IBP training. With an overparameterized assumption, we analyze the convergence of IBP robust training. We show that when using IBP training to train a randomly initialized two-layer ReLU neural network with logistic loss, gradient descent can linearly converge to zero robust training error with a high probability if we have sufficiently small perturbation radius and large network width.
* ICLR 2022
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge