Unifying 3D Representation and Control of Diverse Robots with a Single Camera

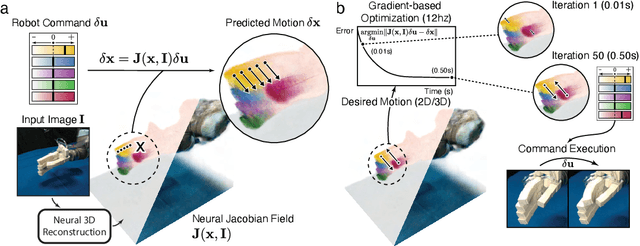
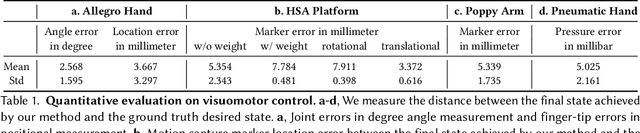
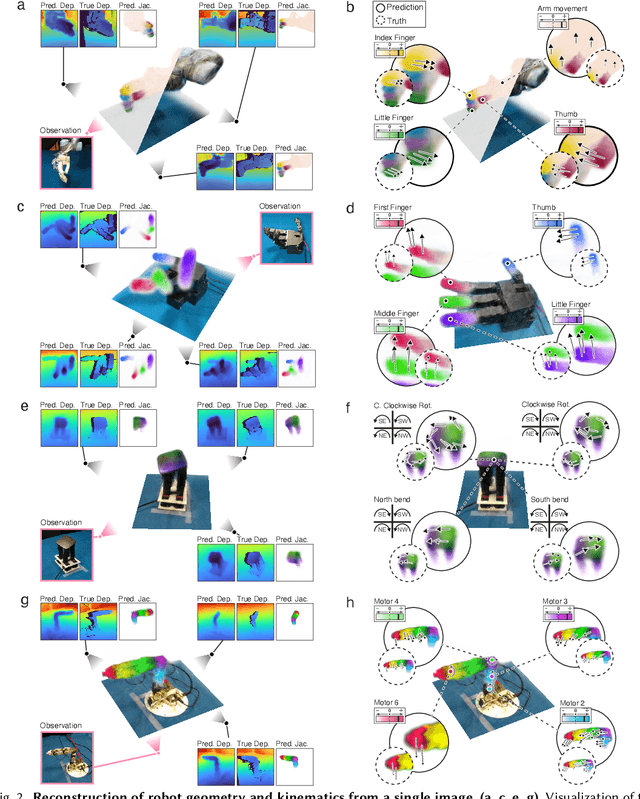
Mirroring the complex structures and diverse functions of natural organisms is a long-standing challenge in robotics. Modern fabrication techniques have dramatically expanded feasible hardware, yet deploying these systems requires control software to translate desired motions into actuator commands. While conventional robots can easily be modeled as rigid links connected via joints, it remains an open challenge to model and control bio-inspired robots that are often multi-material or soft, lack sensing capabilities, and may change their material properties with use. Here, we introduce Neural Jacobian Fields, an architecture that autonomously learns to model and control robots from vision alone. Our approach makes no assumptions about the robot's materials, actuation, or sensing, requires only a single camera for control, and learns to control the robot without expert intervention by observing the execution of random commands. We demonstrate our method on a diverse set of robot manipulators, varying in actuation, materials, fabrication, and cost. Our approach achieves accurate closed-loop control and recovers the causal dynamic structure of each robot. By enabling robot control with a generic camera as the only sensor, we anticipate our work will dramatically broaden the design space of robotic systems and serve as a starting point for lowering the barrier to robotic automation.

Certified Polyhedral Decompositions of Collision-Free Configuration Space

Understanding the geometry of collision-free configuration space (C-free) in the presence of task-space obstacles is an essential ingredient for collision-free motion planning. While it is possible to check for collisions at a point using standard algorithms, to date no practical method exists for computing C-free regions with rigorous certificates due to the complexity of mapping task-space obstacles through the kinematics. In this work, we present the first to our knowledge rigorous method for approximately decomposing a rational parametrization of C-free into certified polyhedral regions. Our method, called C-IRIS (C-space Iterative Regional Inflation by Semidefinite programming), generates large, convex polytopes in a rational parameterization of the configuration space which are rigorously certified to be collision-free. Such regions have been shown to be useful for both optimization-based and randomized motion planning. Based on convex optimization, our method works in arbitrary dimensions, only makes assumptions about the convexity of the obstacles in the task space, and is fast enough to scale to realistic problems in manipulation. We demonstrate our algorithm's ability to fill a non-trivial amount of collision-free C-space in several 2-DOF examples where the C-space can be visualized, as well as the scalability of our algorithm on a 7-DOF KUKA iiwa, a 6-DOF UR3e and 12-DOF bimanual manipulators. An implementation of our algorithm is open-sourced in Drake. We furthermore provide examples of our algorithm in interactive Python notebooks.

Finding and Optimizing Certified, Collision-Free Regions in Configuration Space for Robot Manipulators

Configuration space (C-space) has played a central role in collision-free motion planning, particularly for robot manipulators. While it is possible to check for collisions at a point using standard algorithms, to date no practical method exists for computing collision-free C-space regions with rigorous certificates due to the complexities of mapping task-space obstacles through the kinematics. In this work, we present the first to our knowledge method for generating such regions and certificates through convex optimization. Our method, called C-Iris (C-space Iterative Regional Inflation by Semidefinite programming), generates large, convex polytopes in a rational parametrization of the configuration space which are guaranteed to be collision-free. Such regions have been shown to be useful for both optimization-based and randomized motion planning. Our regions are generated by alternating between two convex optimization problems: (1) a simultaneous search for a maximal-volume ellipse inscribed in a given polytope and a certificate that the polytope is collision-free and (2) a maximal expansion of the polytope away from the ellipse which does not violate the certificate. The volume of the ellipse and size of the polytope are allowed to grow over several iterations while being collision-free by construction. Our method works in arbitrary dimensions, only makes assumptions about the convexity of the obstacles in the task space, and scales to realistic problems in manipulation. We demonstrate our algorithm's ability to fill a non-trivial amount of collision-free C-space in a 3-DOF example where the C-space can be visualized, as well as the scalability of our algorithm on a 7-DOF KUKA iiwa and a 12-DOF bimanual manipulator.