Multi-Query Shortest-Path Problem in Graphs of Convex Sets

The Shortest-Path Problem in Graph of Convex Sets (SPP in GCS) is a recently developed optimization framework that blends discrete and continuous decision making. Many relevant problems in robotics, such as collision-free motion planning, can be cast and solved as an SPP in GCS, yielding lower-cost solutions and faster runtimes than state-of-the-art algorithms. In this paper, we are motivated by motion planning of robot arms that must operate swiftly in static environments. We consider a multi-query extension of the SPP in GCS, where the goal is to efficiently precompute optimal paths between given sets of initial and target conditions. Our solution consists of two stages. Offline, we use semidefinite programming to compute a coarse lower bound on the problem's cost-to-go function. Then, online, this lower bound is used to incrementally generate feasible paths by solving short-horizon convex programs. For a robot arm with seven joints, our method designs higher quality trajectories up to two orders of magnitude faster than existing motion planners.

Towards Tight Convex Relaxations for Contact-Rich Manipulation

We present a method for global motion planning of robotic systems that interact with the environment through contacts. Our method directly handles the hybrid nature of such tasks using tools from convex optimization. We formulate the motion-planning problem as a shortest-path problem in a graph of convex sets, where a path in the graph corresponds to a contact sequence and a convex set models the quasi-static dynamics within a fixed contact mode. For each contact mode, we use semidefinite programming to relax the nonconvex dynamics that results from the simultaneous optimization of the object's pose, contact locations, and contact forces. The result is a tight convex relaxation of the overall planning problem, that can be efficiently solved and quickly rounded to find a feasible contact-rich trajectory. As a first application of this technique, we focus on the task of planar pushing. Exhaustive experiments show that our convex-optimization method generates plans that are consistently within a small percentage of the global optimum. We demonstrate the quality of these plans on a real robotic system.

Certifying Bimanual RRT Motion Plans in a Second

We present an efficient method for certifying non-collision for piecewise-polynomial motion plans in algebraic reparametrizations of configuration space. Such motion plans include those generated by popular randomized methods including RRTs and PRMs, as well as those generated by many methods in trajectory optimization. Based on Sums-of-Squares optimization, our method provides exact, rigorous certificates of non-collision; it can never falsely claim that a motion plan containing collisions is collision-free. We demonstrate that our formulation is practical for real world deployment, certifying the safety of a twelve degree of freedom motion plan in just over a second. Moreover, the method is capable of discriminating the safety or lack thereof of two motion plans which differ by only millimeters.

Approximating Robot Configuration Spaces with few Convex Sets using Clique Covers of Visibility Graphs

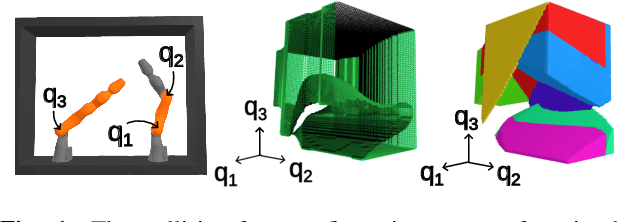
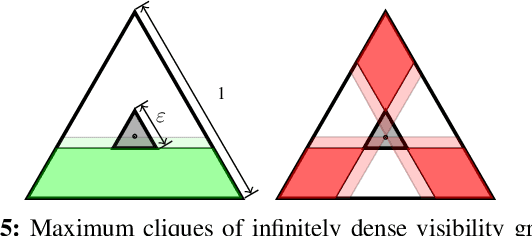
Many computations in robotics can be dramatically accelerated if the robot configuration space is described as a collection of simple sets. For example, recently developed motion planners rely on a convex decomposition of the free space to design collision-free trajectories using fast convex optimization. In this work, we present an efficient method for approximately covering complex configuration spaces with a small number of polytopes. The approach constructs a visibility graph using sampling and generates a clique cover of this graph to find clusters of samples that have mutual line of sight. These clusters are then inflated into large, full-dimensional, polytopes. We evaluate our method on a variety of robotic systems and show that it consistently covers larger portions of free configuration space, with fewer polytopes, and in a fraction of the time compared to previous methods.

Suboptimal Controller Synthesis for Cart-Poles and Quadrotors via Sums-of-Squares

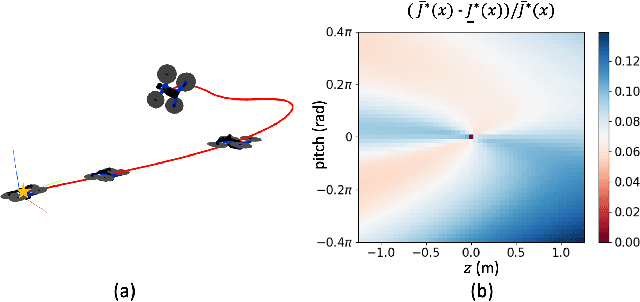
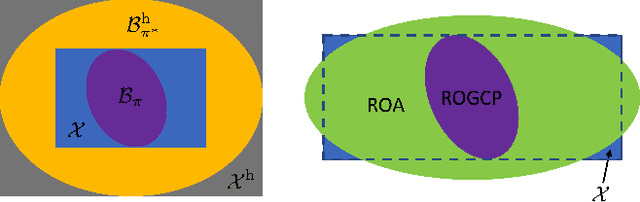
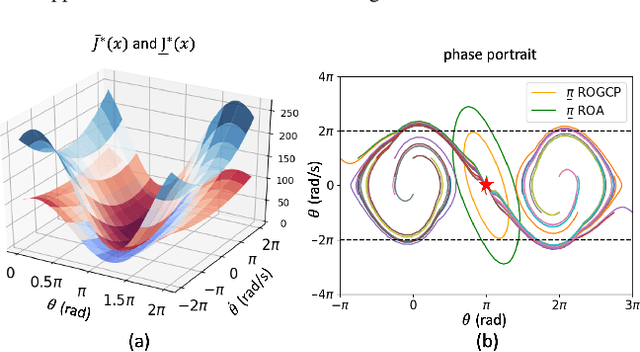
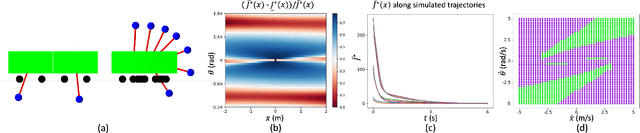
Sums-of-squares (SOS) optimization is a promising tool to synthesize certifiable controllers, but most examples to date have been limited to relatively simple systems. Here we demonstrate that SOS can synthesize controllers with bounded suboptimal performance for various underactuated robotic systems by finding good approximations of the value function. We summarize a unified SOS framework to synthesize both under- and over- approximations of the value function for continuous-time, control-affine systems, use these approximations to generate suboptimal controllers, and perform regional analysis on the closed-loop system driven by these controllers. We then extend the formulation to handle hybrid systems with contacts. We demonstrate that our method can generate tight under- and over- approximations of the value function with low-degree polynomials, which are used to provide stabilizing controllers for continuous-time systems including the inverted pendulum, the cart-pole, and the 3D quadrotor as well as a hybrid system, the planar pusher. To the best of our knowledge, this is the first time that a SOS-based time-invariant controller can swing up and stabilize a cart-pole, and push the planar slider to the desired pose.

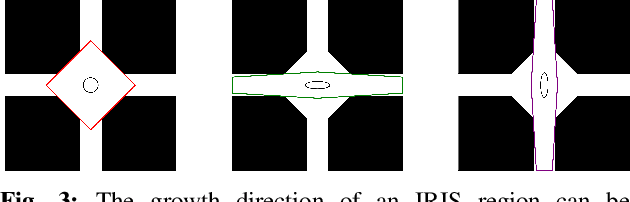
Certified Polyhedral Decompositions of Collision-Free Configuration Space

Understanding the geometry of collision-free configuration space (C-free) in the presence of task-space obstacles is an essential ingredient for collision-free motion planning. While it is possible to check for collisions at a point using standard algorithms, to date no practical method exists for computing C-free regions with rigorous certificates due to the complexity of mapping task-space obstacles through the kinematics. In this work, we present the first to our knowledge rigorous method for approximately decomposing a rational parametrization of C-free into certified polyhedral regions. Our method, called C-IRIS (C-space Iterative Regional Inflation by Semidefinite programming), generates large, convex polytopes in a rational parameterization of the configuration space which are rigorously certified to be collision-free. Such regions have been shown to be useful for both optimization-based and randomized motion planning. Based on convex optimization, our method works in arbitrary dimensions, only makes assumptions about the convexity of the obstacles in the task space, and is fast enough to scale to realistic problems in manipulation. We demonstrate our algorithm's ability to fill a non-trivial amount of collision-free C-space in several 2-DOF examples where the C-space can be visualized, as well as the scalability of our algorithm on a 7-DOF KUKA iiwa, a 6-DOF UR3e and 12-DOF bimanual manipulators. An implementation of our algorithm is open-sourced in Drake. We furthermore provide examples of our algorithm in interactive Python notebooks.

Finding and Optimizing Certified, Collision-Free Regions in Configuration Space for Robot Manipulators

Configuration space (C-space) has played a central role in collision-free motion planning, particularly for robot manipulators. While it is possible to check for collisions at a point using standard algorithms, to date no practical method exists for computing collision-free C-space regions with rigorous certificates due to the complexities of mapping task-space obstacles through the kinematics. In this work, we present the first to our knowledge method for generating such regions and certificates through convex optimization. Our method, called C-Iris (C-space Iterative Regional Inflation by Semidefinite programming), generates large, convex polytopes in a rational parametrization of the configuration space which are guaranteed to be collision-free. Such regions have been shown to be useful for both optimization-based and randomized motion planning. Our regions are generated by alternating between two convex optimization problems: (1) a simultaneous search for a maximal-volume ellipse inscribed in a given polytope and a certificate that the polytope is collision-free and (2) a maximal expansion of the polytope away from the ellipse which does not violate the certificate. The volume of the ellipse and size of the polytope are allowed to grow over several iterations while being collision-free by construction. Our method works in arbitrary dimensions, only makes assumptions about the convexity of the obstacles in the task space, and scales to realistic problems in manipulation. We demonstrate our algorithm's ability to fill a non-trivial amount of collision-free C-space in a 3-DOF example where the C-space can be visualized, as well as the scalability of our algorithm on a 7-DOF KUKA iiwa and a 12-DOF bimanual manipulator.