Multi-Query Shortest-Path Problem in Graphs of Convex Sets

The Shortest-Path Problem in Graph of Convex Sets (SPP in GCS) is a recently developed optimization framework that blends discrete and continuous decision making. Many relevant problems in robotics, such as collision-free motion planning, can be cast and solved as an SPP in GCS, yielding lower-cost solutions and faster runtimes than state-of-the-art algorithms. In this paper, we are motivated by motion planning of robot arms that must operate swiftly in static environments. We consider a multi-query extension of the SPP in GCS, where the goal is to efficiently precompute optimal paths between given sets of initial and target conditions. Our solution consists of two stages. Offline, we use semidefinite programming to compute a coarse lower bound on the problem's cost-to-go function. Then, online, this lower bound is used to incrementally generate feasible paths by solving short-horizon convex programs. For a robot arm with seven joints, our method designs higher quality trajectories up to two orders of magnitude faster than existing motion planners.

GCS*: Forward Heuristic Search on Implicit Graphs of Convex Sets

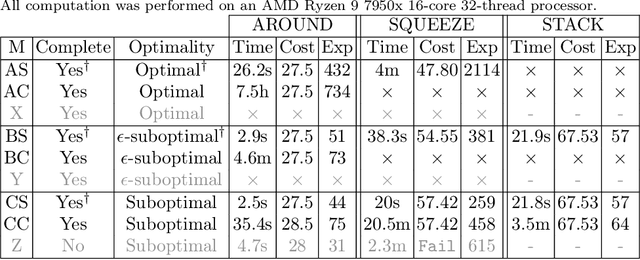
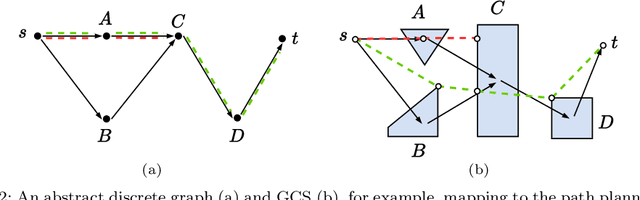
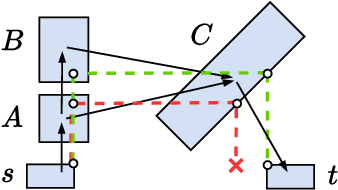
We consider large-scale, implicit-search-based solutions to the Shortest Path Problems on Graphs of Convex Sets (GCS). We propose GCS*, a forward heuristic search algorithm that generalizes A* search to the GCS setting, where a continuous-valued decision is made at each graph vertex, and constraints across graph edges couple these decisions, influencing costs and feasibility. Such mixed discrete-continuous planning is needed in many domains, including motion planning around obstacles and planning through contact. This setting provides a unique challenge for best-first search algorithms: the cost and feasibility of a path depend on continuous-valued points chosen along the entire path. We show that by pruning paths that are cost-dominated over their entire terminal vertex, GCS* can search efficiently while still guaranteeing cost optimality and completeness. To find satisficing solutions quickly, we also present a complete but suboptimal variation, pruning instead reachability-dominated paths. We implement these checks using polyhedral-containment or sampling-based methods. The sampling-based implementation is probabilistically complete and asymptotically cost optimal, and performs effectively even with minimal samples in practice. We demonstrate GCS* on planar pushing tasks where the combinatorial explosion of contact modes renders prior methods intractable and show it performs favorably compared to the state-of-the-art. Project website: https://shaoyuan.cc/research/gcs-star/