Faster Algorithms for Growing Collision-Free Convex Polytopes in Robot Configuration Space

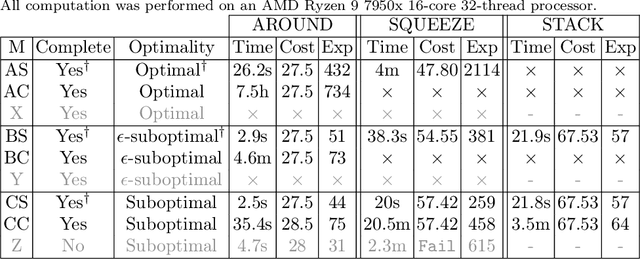
We propose two novel algorithms for constructing convex collision-free polytopes in robot configuration space. Finding these polytopes enables the application of stronger motion-planning frameworks such as trajectory optimization with Graphs of Convex Sets [1] and is currently a major roadblock in the adoption of these approaches. In this paper, we build upon IRIS-NP (Iterative Regional Inflation by Semidefinite & Nonlinear Programming) [2] to significantly improve tunability, runtimes, and scaling to complex environments. IRIS-NP uses nonlinear programming paired with uniform random initialization to find configurations on the boundary of the free configuration space. Our key insight is that finding near-by configuration-space obstacles using sampling is inexpensive and greatly accelerates region generation. We propose two algorithms using such samples to either employ nonlinear programming more efficiently (IRIS-NP2 ) or circumvent it altogether using a massively-parallel zero-order optimization strategy (IRIS-ZO). We also propose a termination condition that controls the probability of exceeding a user-specified permissible fraction-in-collision, eliminating a significant source of tuning difficulty in IRIS-NP. We compare performance across eight robot environments, showing that IRIS-ZO achieves an order-of-magnitude speed advantage over IRIS-NP. IRISNP2, also significantly faster than IRIS-NP, builds larger polytopes using fewer hyperplanes, enabling faster downstream computation. Website: https://sites.google.com/view/fastiris

GCS*: Forward Heuristic Search on Implicit Graphs of Convex Sets

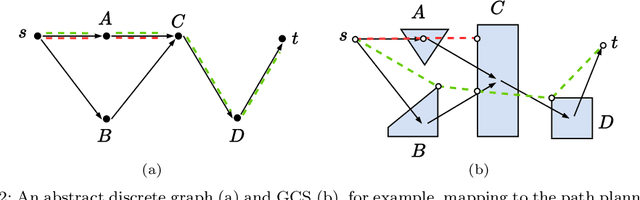
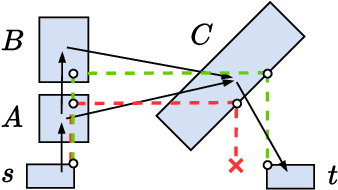
We consider large-scale, implicit-search-based solutions to the Shortest Path Problems on Graphs of Convex Sets (GCS). We propose GCS*, a forward heuristic search algorithm that generalizes A* search to the GCS setting, where a continuous-valued decision is made at each graph vertex, and constraints across graph edges couple these decisions, influencing costs and feasibility. Such mixed discrete-continuous planning is needed in many domains, including motion planning around obstacles and planning through contact. This setting provides a unique challenge for best-first search algorithms: the cost and feasibility of a path depend on continuous-valued points chosen along the entire path. We show that by pruning paths that are cost-dominated over their entire terminal vertex, GCS* can search efficiently while still guaranteeing cost optimality and completeness. To find satisficing solutions quickly, we also present a complete but suboptimal variation, pruning instead reachability-dominated paths. We implement these checks using polyhedral-containment or sampling-based methods. The sampling-based implementation is probabilistically complete and asymptotically cost optimal, and performs effectively even with minimal samples in practice. We demonstrate GCS* on planar pushing tasks where the combinatorial explosion of contact modes renders prior methods intractable and show it performs favorably compared to the state-of-the-art. Project website: https://shaoyuan.cc/research/gcs-star/

Parallel-Jaw Gripper and Grasp Co-Optimization for Sets of Planar Objects

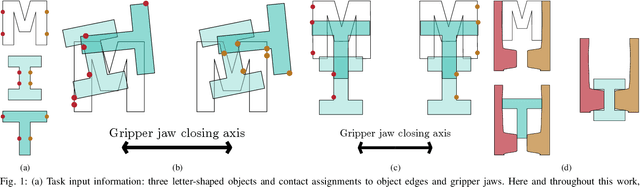
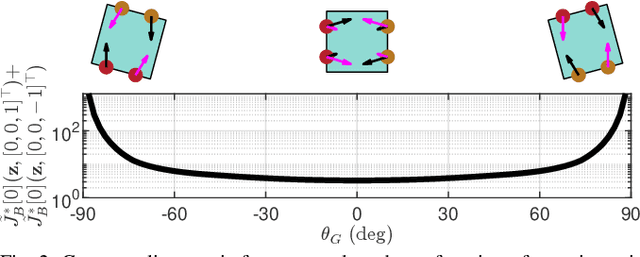
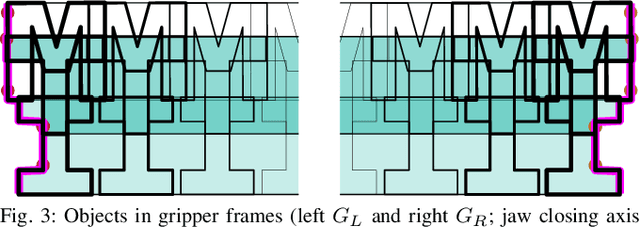
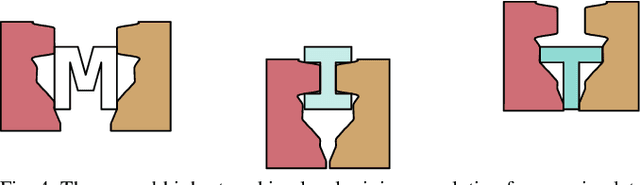
We propose a framework for optimizing a planar parallel-jaw gripper for use with multiple objects. While optimizing general-purpose grippers and contact locations for grasps are both well studied, co-optimizing grasps and the gripper geometry to execute them receives less attention. As such, our framework synthesizes grippers optimized to stably grasp sets of polygonal objects. Given a fixed number of contacts and their assignments to object faces and gripper jaws, our framework optimizes contact locations along these faces, gripper pose for each grasp, and gripper shape. Our key insights are to pose shape and contact constraints in frames fixed to the gripper jaws, and to leverage the linearity of constraints in our grasp stability and gripper shape models via an augmented Lagrangian formulation. Together, these enable a tractable nonlinear program implementation. We apply our method to several examples. The first illustrative problem shows the discovery of a geometrically simple solution where possible. In another, space is constrained, forcing multiple objects to be contacted by the same features as each other. Finally a toolset-grasping example shows that our framework applies to complex, real-world objects. We provide a physical experiment of the toolset grasps.