Planning Shorter Paths in Graphs of Convex Sets by Undistorting Parametrized Configuration Spaces

Optimization based motion planning provides a useful modeling framework through various costs and constraints. Using Graph of Convex Sets (GCS) for trajectory optimization gives guarantees of feasibility and optimality by representing configuration space as the finite union of convex sets. Nonlinear parametrizations can be used to extend this technique to handle cases such as kinematic loops, but this distorts distances, such that solving with convex objectives will yield paths that are suboptimal in the original space. We present a method to extend GCS to nonconvex objectives, allowing us to "undistort" the optimization landscape while maintaining feasibility guarantees. We demonstrate our method's efficacy on three different robotic planning domains: a bimanual robot moving an object with both arms, the set of 3D rotations using Euler angles, and a rational parametrization of kinematics that enables certifying regions as collision free. Across the board, our method significantly improves path length and trajectory duration with only a minimal increase in runtime. Website: https://shrutigarg914.github.io/pgd-gcs-results/

Faster Algorithms for Growing Collision-Free Convex Polytopes in Robot Configuration Space

We propose two novel algorithms for constructing convex collision-free polytopes in robot configuration space. Finding these polytopes enables the application of stronger motion-planning frameworks such as trajectory optimization with Graphs of Convex Sets [1] and is currently a major roadblock in the adoption of these approaches. In this paper, we build upon IRIS-NP (Iterative Regional Inflation by Semidefinite & Nonlinear Programming) [2] to significantly improve tunability, runtimes, and scaling to complex environments. IRIS-NP uses nonlinear programming paired with uniform random initialization to find configurations on the boundary of the free configuration space. Our key insight is that finding near-by configuration-space obstacles using sampling is inexpensive and greatly accelerates region generation. We propose two algorithms using such samples to either employ nonlinear programming more efficiently (IRIS-NP2 ) or circumvent it altogether using a massively-parallel zero-order optimization strategy (IRIS-ZO). We also propose a termination condition that controls the probability of exceeding a user-specified permissible fraction-in-collision, eliminating a significant source of tuning difficulty in IRIS-NP. We compare performance across eight robot environments, showing that IRIS-ZO achieves an order-of-magnitude speed advantage over IRIS-NP. IRISNP2, also significantly faster than IRIS-NP, builds larger polytopes using fewer hyperplanes, enabling faster downstream computation. Website: https://sites.google.com/view/fastiris

Constrained Bimanual Planning with Analytic Inverse Kinematics

In order for a bimanual robot to manipulate an object that is held by both hands, it must construct motion plans such that the transformation between its end effectors remains fixed. This amounts to complicated nonlinear equality constraints in the configuration space, which are difficult for trajectory optimizers. In addition, the set of feasible configurations becomes a measure zero set, which presents a challenge to sampling-based motion planners. We leverage an analytic solution to the inverse kinematics problem to parametrize the configuration space, resulting in a lower-dimensional representation where the set of valid configurations has positive measure. We describe how to use this parametrization with existing algorithms for motion planning, including sampling-based approaches, trajectory optimizers, and techniques that plan through convex inner-approximations of collision-free space.

Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

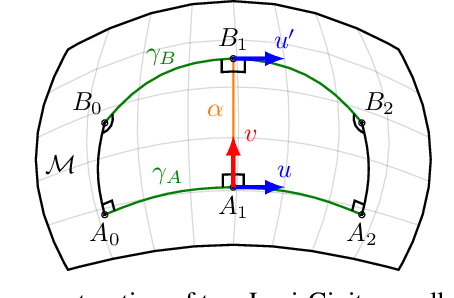
Computing optimal, collision-free trajectories for high-dimensional systems is a challenging problem. Sampling-based planners struggle with the dimensionality, whereas trajectory optimizers may get stuck in local minima due to inherent nonconvexities in the optimization landscape. The use of mixed-integer programming to encapsulate these nonconvexities and find globally optimal trajectories has recently shown great promise, thanks in part to tight convex relaxations and efficient approximation strategies that greatly reduce runtimes. These approaches were previously limited to Euclidean configuration spaces, precluding their use with mobile bases or continuous revolute joints. In this paper, we handle such scenarios by modeling configuration spaces as Riemannian manifolds, and we describe a reduction procedure for the zero-curvature case to a mixed-integer convex optimization problem. We demonstrate our results on various robot platforms, including producing efficient collision-free trajectories for a PR2 bimanual mobile manipulator.

Topologically-Informed Atlas Learning

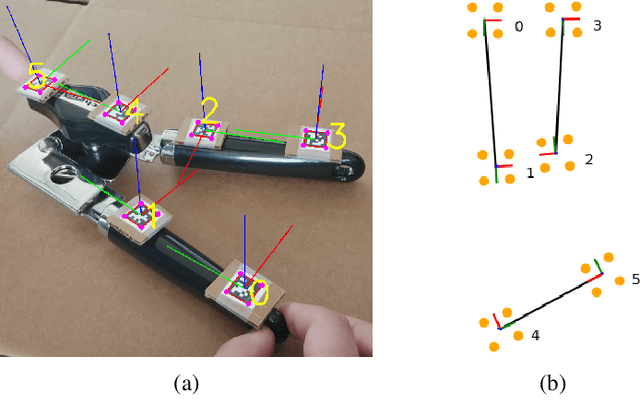
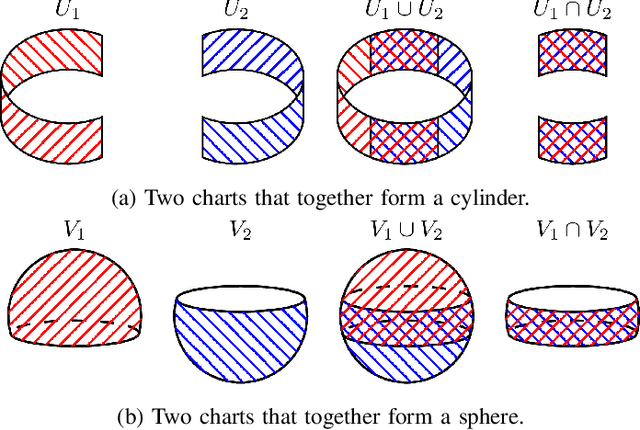
We present a new technique that enables manifold learning to accurately embed data manifolds that contain holes, without discarding any topological information. Manifold learning aims to embed high dimensional data into a lower dimensional Euclidean space by learning a coordinate chart, but it requires that the entire manifold can be embedded in a single chart. This is impossible for manifolds with holes. In such cases, it is necessary to learn an atlas: a collection of charts that collectively cover the entire manifold. We begin with many small charts, and combine them in a bottom-up approach, where charts are only combined if doing so will not introduce problematic topological features. When it is no longer possible to combine any charts, each chart is individually embedded with standard manifold learning techniques, completing the construction of the atlas. We show the efficacy of our method by constructing atlases for challenging synthetic manifolds; learning human motion embeddings from motion capture data; and learning kinematic models of articulated objects.