Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

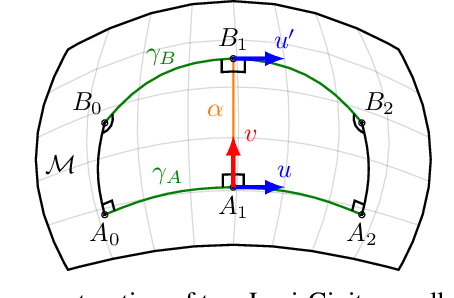
Computing optimal, collision-free trajectories for high-dimensional systems is a challenging problem. Sampling-based planners struggle with the dimensionality, whereas trajectory optimizers may get stuck in local minima due to inherent nonconvexities in the optimization landscape. The use of mixed-integer programming to encapsulate these nonconvexities and find globally optimal trajectories has recently shown great promise, thanks in part to tight convex relaxations and efficient approximation strategies that greatly reduce runtimes. These approaches were previously limited to Euclidean configuration spaces, precluding their use with mobile bases or continuous revolute joints. In this paper, we handle such scenarios by modeling configuration spaces as Riemannian manifolds, and we describe a reduction procedure for the zero-curvature case to a mixed-integer convex optimization problem. We demonstrate our results on various robot platforms, including producing efficient collision-free trajectories for a PR2 bimanual mobile manipulator.

Growing Convex Collision-Free Regions in Configuration Space using Nonlinear Programming

One of the most difficult parts of motion planning in configuration space is ensuring a trajectory does not collide with task-space obstacles in the environment. Generating regions that are convex and collision free in configuration space can separate the computational burden of collision checking from motion planning. To that end, we propose an extension to IRIS (Iterative Regional Inflation by Semidefinite programming) [5] that allows it to operate in configuration space. Our algorithm, IRIS-NP (Iterative Regional Inflation by Semidefinite & Nonlinear Programming), uses nonlinear optimization to add the separating hyperplanes, enabling support for more general nonlinear constraints. Developed in parallel to Amice et al. [1], IRIS-NP trades rigorous certification that regions are collision free for probabilistic certification and the benefit of faster region generation in the configuration-space coordinates. IRIS-NP also provides a solid initialization to C-IRIS to reduce the number of iterations required for certification. We demonstrate that IRIS-NP can scale to a dual-arm manipulator and can handle additional nonlinear constraints using the same machinery. Finally, we show ablations of elements of our implementation to demonstrate their importance.

Motion Planning around Obstacles with Convex Optimization

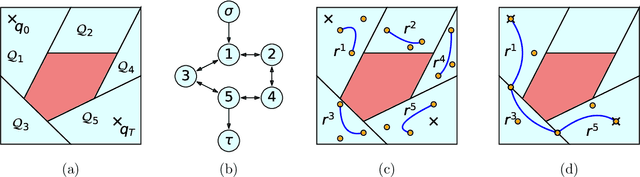
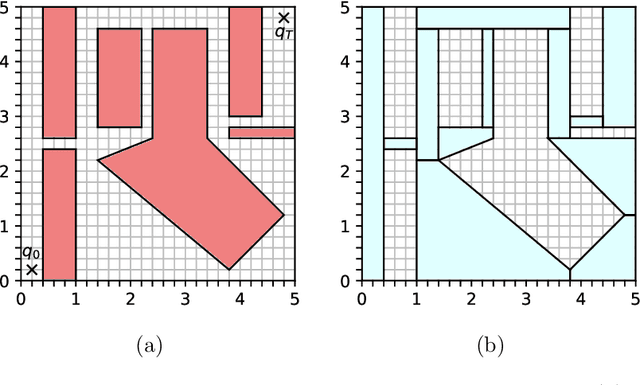
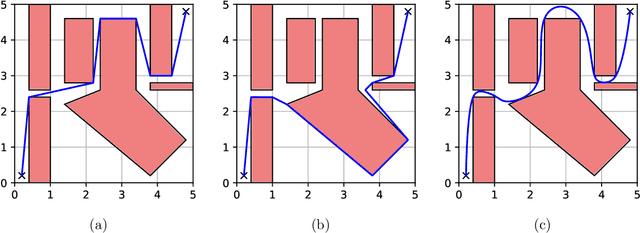
Trajectory optimization offers mature tools for motion planning in high-dimensional spaces under dynamic constraints. However, when facing complex configuration spaces, cluttered with obstacles, roboticists typically fall back to sampling-based planners that struggle in very high dimensions and with continuous differential constraints. Indeed, obstacles are the source of many textbook examples of problematic nonconvexities in the trajectory-optimization problem. Here we show that convex optimization can, in fact, be used to reliably plan trajectories around obstacles. Specifically, we consider planning problems with collision-avoidance constraints, as well as cost penalties and hard constraints on the shape, the duration, and the velocity of the trajectory. Combining the properties of B\'ezier curves with a recently-proposed framework for finding shortest paths in Graphs of Convex Sets (GCS), we formulate the planning problem as a compact mixed-integer optimization. In stark contrast with existing mixed-integer planners, the convex relaxation of our programs is very tight, and a cheap rounding of its solution is typically sufficient to design globally-optimal trajectories. This reduces the mixed-integer program back to a simple convex optimization, and automatically provides optimality bounds for the planned trajectories. We name the proposed planner GCS, after its underlying optimization framework. We demonstrate GCS in simulation on a variety of robotic platforms, including a quadrotor flying through buildings and a dual-arm manipulator (with fourteen degrees of freedom) moving in a confined space. Using numerical experiments on a seven-degree-of-freedom manipulator, we show that GCS can outperform widely-used sampling-based planners by finding higher-quality trajectories in less time.