Optimal Constrained Task Planning as Mixed Integer Programming

For robots to successfully execute tasks assigned to them, they must be capable of planning the right sequence of actions. These actions must be both optimal with respect to a specified objective and satisfy whatever constraints exist in their world. We propose an approach for robot task planning that is capable of planning the optimal sequence of grounded actions to accomplish a task given a specific objective function while satisfying all specified numerical constraints. Our approach accomplishes this by encoding the entire task planning problem as a single mixed integer convex program, which it then solves using an off-the-shelf Mixed Integer Programming solver. We evaluate our approach on several mobile manipulation tasks in both simulation and on a physical humanoid robot. Our approach is able to consistently produce optimal plans while accounting for all specified numerical constraints in the mobile manipulation tasks. Open-source implementations of the components of our approach as well as videos of robots executing planned grounded actions in both simulation and the physical world can be found at this url: https://adubredu.github.io/gtpmip

DANLI: Deliberative Agent for Following Natural Language Instructions

Recent years have seen an increasing amount of work on embodied AI agents that can perform tasks by following human language instructions. However, most of these agents are reactive, meaning that they simply learn and imitate behaviors encountered in the training data. These reactive agents are insufficient for long-horizon complex tasks. To address this limitation, we propose a neuro-symbolic deliberative agent that, while following language instructions, proactively applies reasoning and planning based on its neural and symbolic representations acquired from past experience (e.g., natural language and egocentric vision). We show that our deliberative agent achieves greater than 70% improvement over reactive baselines on the challenging TEACh benchmark. Moreover, the underlying reasoning and planning processes, together with our modular framework, offer impressive transparency and explainability to the behaviors of the agent. This enables an in-depth understanding of the agent's capabilities, which shed light on challenges and opportunities for future embodied agents for instruction following. The code is available at https://github.com/sled-group/DANLI.

Probabilistic Inference in Planning for Partially Observable Long Horizon Problems

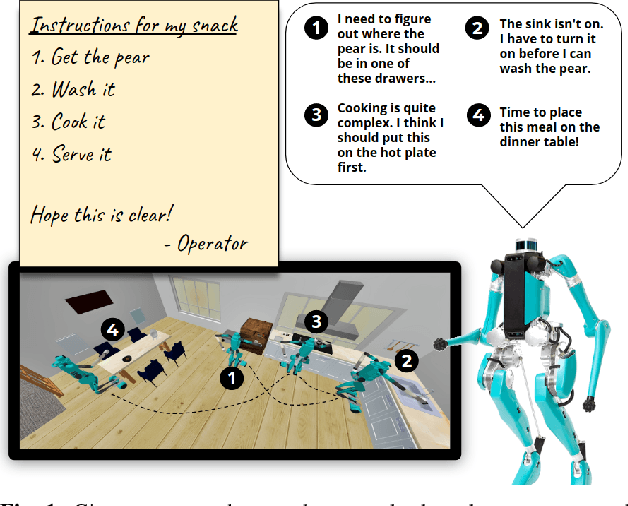
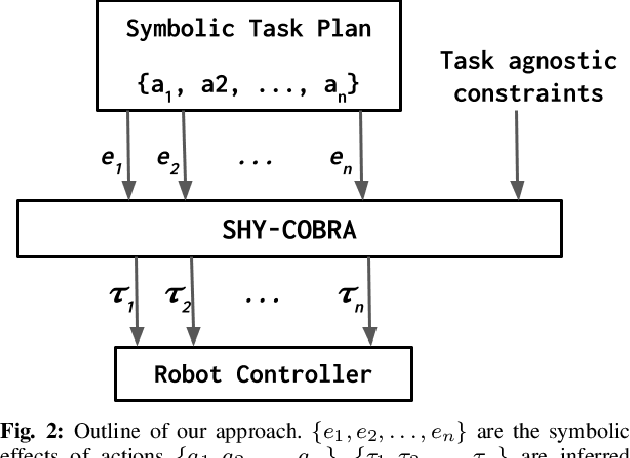
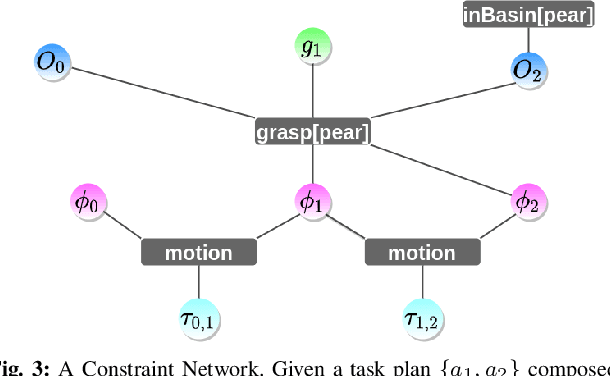
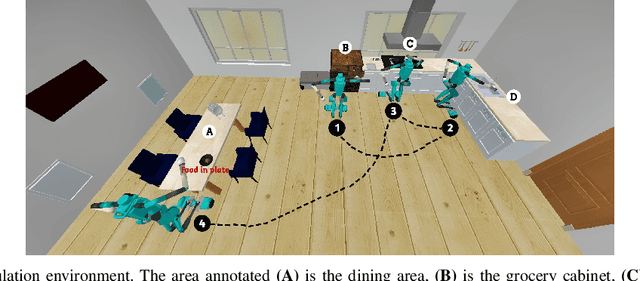
For autonomous service robots to successfully perform long horizon tasks in the real world, they must act intelligently in partially observable environments. Most Task and Motion Planning approaches assume full observability of their state space, making them ineffective in stochastic and partially observable domains that reflect the uncertainties in the real world. We propose an online planning and execution approach for performing long horizon tasks in partially observable domains. Given the robot's belief and a plan skeleton composed of symbolic actions, our approach grounds each symbolic action by inferring continuous action parameters needed to execute the plan successfully. To achieve this, we formulate the problem of joint inference of action parameters as a Hybrid Constraint Satisfaction Problem (H-CSP) and solve the H-CSP using Belief Propagation. The robot executes the resulting parameterized actions, updates its belief of the world and replans when necessary. Our approach is able to efficiently solve partially observable tasks in a realistic kitchen simulation environment. Our approach outperformed an adaptation of the state-of-the-art method across our experiments.

Topologically-Informed Atlas Learning

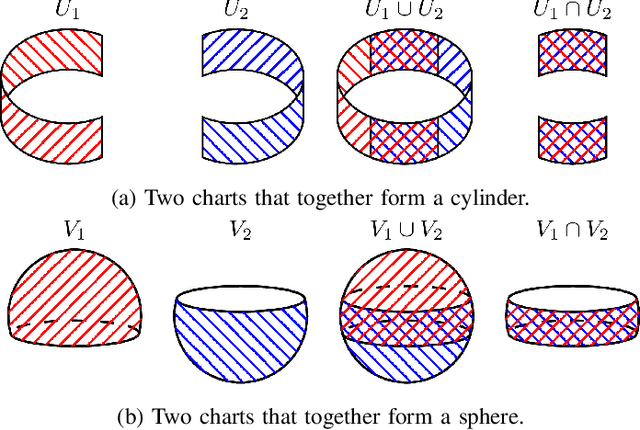
We present a new technique that enables manifold learning to accurately embed data manifolds that contain holes, without discarding any topological information. Manifold learning aims to embed high dimensional data into a lower dimensional Euclidean space by learning a coordinate chart, but it requires that the entire manifold can be embedded in a single chart. This is impossible for manifolds with holes. In such cases, it is necessary to learn an atlas: a collection of charts that collectively cover the entire manifold. We begin with many small charts, and combine them in a bottom-up approach, where charts are only combined if doing so will not introduce problematic topological features. When it is no longer possible to combine any charts, each chart is individually embedded with standard manifold learning techniques, completing the construction of the atlas. We show the efficacy of our method by constructing atlases for challenging synthetic manifolds; learning human motion embeddings from motion capture data; and learning kinematic models of articulated objects.