Towards Practical Finite Sample Bounds for Motion Planning in TAMP

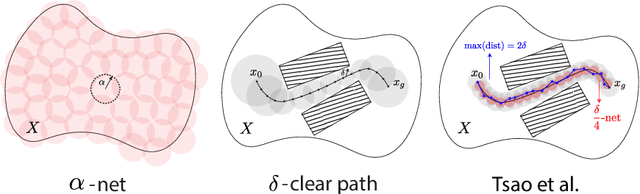
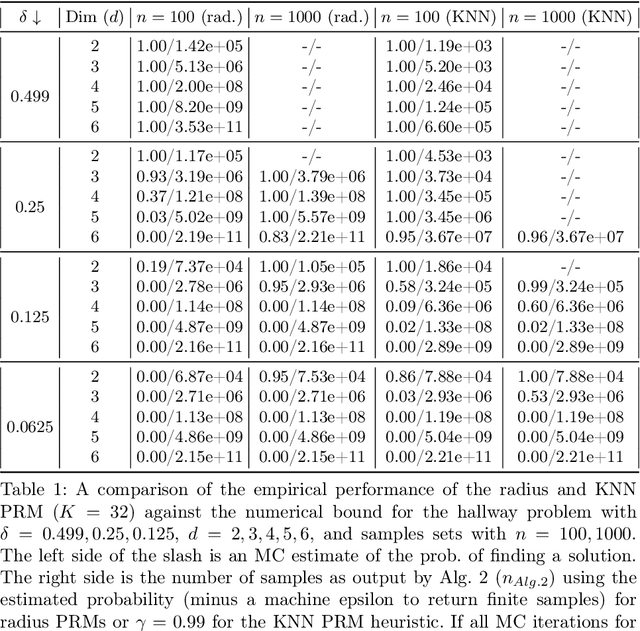
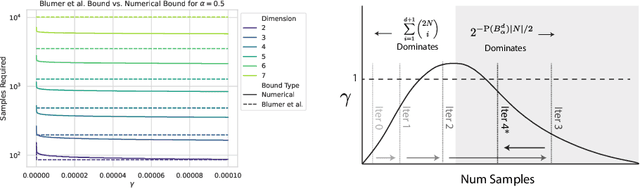
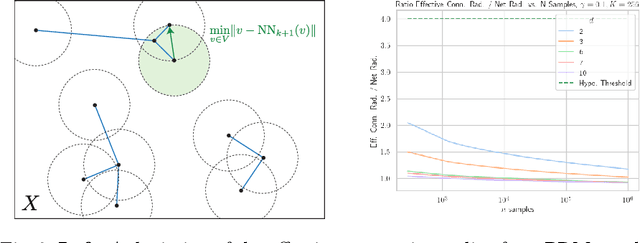
When using sampling-based motion planners, such as PRMs, in configuration spaces, it is difficult to determine how many samples are required for the PRM to find a solution consistently. This is relevant in Task and Motion Planning (TAMP), where many motion planning problems must be solved in sequence. We attempt to solve this problem by proving an upper bound on the number of samples that are sufficient, with high probability, to find a solution by drawing on prior work in deterministic sampling and sample complexity theory. We also introduce a numerical algorithm to compute a tighter number of samples based on the proof of the sample complexity theorem we apply to derive our bound. Our experiments show that our numerical bounding algorithm is tight within two orders of magnitude on planar planning problems and becomes looser as the problem's dimensionality increases. When deployed as a heuristic to schedule samples in a TAMP planner, we also observe planning time improvements in planar problems. While our experiments show much work remains to tighten our bounds, the ideas presented in this paper are a step towards a practical sample bound.

Constrained Bimanual Planning with Analytic Inverse Kinematics

In order for a bimanual robot to manipulate an object that is held by both hands, it must construct motion plans such that the transformation between its end effectors remains fixed. This amounts to complicated nonlinear equality constraints in the configuration space, which are difficult for trajectory optimizers. In addition, the set of feasible configurations becomes a measure zero set, which presents a challenge to sampling-based motion planners. We leverage an analytic solution to the inverse kinematics problem to parametrize the configuration space, resulting in a lower-dimensional representation where the set of valid configurations has positive measure. We describe how to use this parametrization with existing algorithms for motion planning, including sampling-based approaches, trajectory optimizers, and techniques that plan through convex inner-approximations of collision-free space.

Constrained Dynamic Movement Primitives for Safe Learning of Motor Skills

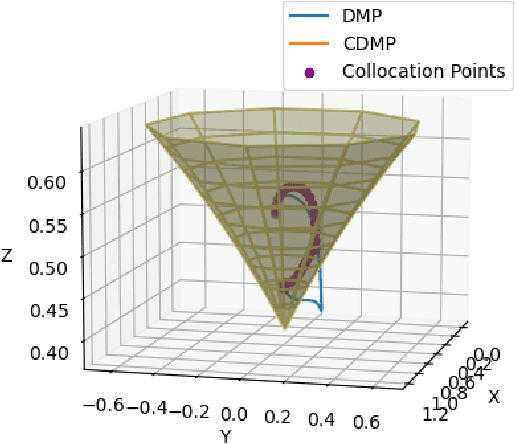
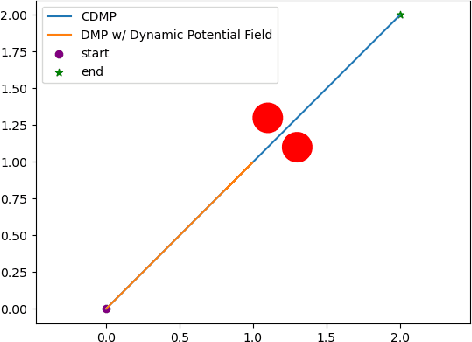
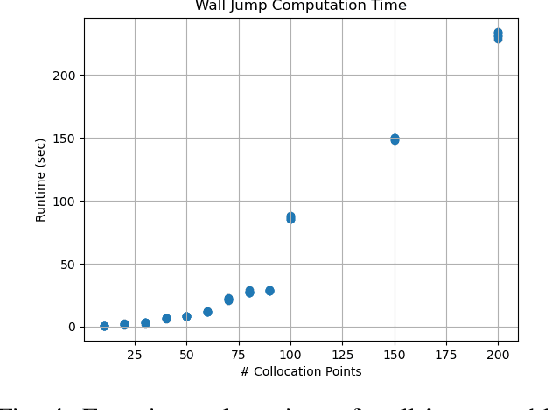
Dynamic movement primitives are widely used for learning skills which can be demonstrated to a robot by a skilled human or controller. While their generalization capabilities and simple formulation make them very appealing to use, they possess no strong guarantees to satisfy operational safety constraints for a task. In this paper, we present constrained dynamic movement primitives (CDMP) which can allow for constraint satisfaction in the robot workspace. We present a formulation of a non-linear optimization to perturb the DMP forcing weights regressed by locally-weighted regression to admit a Zeroing Barrier Function (ZBF), which certifies workspace constraint satisfaction. We demonstrate the proposed CDMP under different constraints on the end-effector movement such as obstacle avoidance and workspace constraints on a physical robot. A video showing the implementation of the proposed algorithm using different manipulators in different environments could be found here https://youtu.be/hJegJJkJfys.

RMPs for Safe Impedance Control in Contact-Rich Manipulation

Variable impedance control in operation-space is a promising approach to learning contact-rich manipulation behaviors. One of the main challenges with this approach is producing a manipulation behavior that ensures the safety of the arm and the environment. Such behavior is typically implemented via a reward function that penalizes unsafe actions (e.g. obstacle collision, joint limit extension), but that approach is not always effective and does not result in behaviors that can be reused in slightly different environments. We show how to combine Riemannian Motion Policies, a class of policies that dynamically generate motion in the presence of safety and collision constraints, with variable impedance operation-space control to learn safer contact-rich manipulation behaviors.