Towards Practical Finite Sample Bounds for Motion Planning in TAMP
Paper and Code
Jul 24, 2024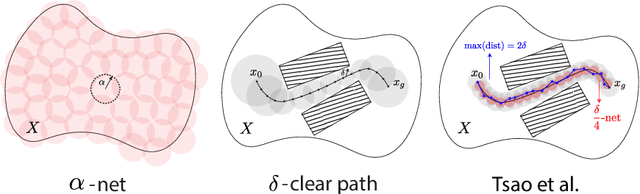
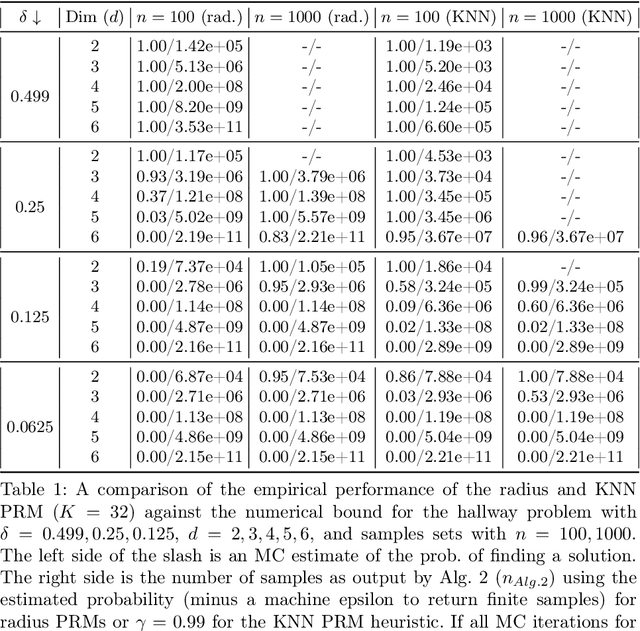
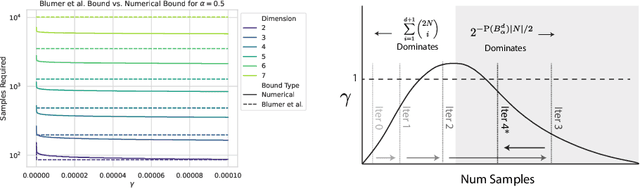
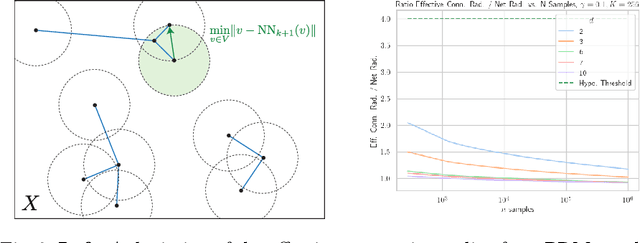
When using sampling-based motion planners, such as PRMs, in configuration spaces, it is difficult to determine how many samples are required for the PRM to find a solution consistently. This is relevant in Task and Motion Planning (TAMP), where many motion planning problems must be solved in sequence. We attempt to solve this problem by proving an upper bound on the number of samples that are sufficient, with high probability, to find a solution by drawing on prior work in deterministic sampling and sample complexity theory. We also introduce a numerical algorithm to compute a tighter number of samples based on the proof of the sample complexity theorem we apply to derive our bound. Our experiments show that our numerical bounding algorithm is tight within two orders of magnitude on planar planning problems and becomes looser as the problem's dimensionality increases. When deployed as a heuristic to schedule samples in a TAMP planner, we also observe planning time improvements in planar problems. While our experiments show much work remains to tighten our bounds, the ideas presented in this paper are a step towards a practical sample bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge