Arvind Raghunathan
Hierarchical Contact-Rich Trajectory Optimization for Multi-Modal Manipulation using Tight Convex Relaxations
Mar 11, 2025
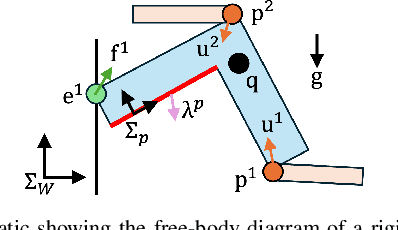
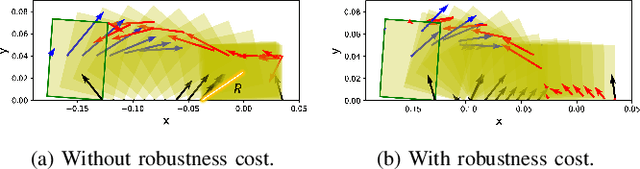
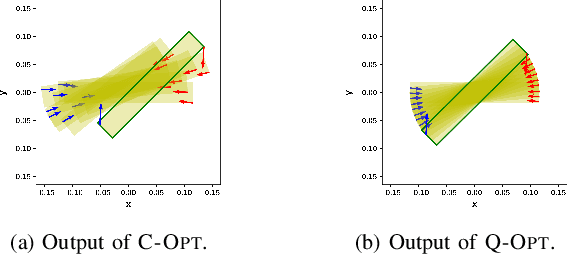
Abstract:Designing trajectories for manipulation through contact is challenging as it requires reasoning of object \& robot trajectories as well as complex contact sequences simultaneously. In this paper, we present a novel framework for simultaneously designing trajectories of robots, objects, and contacts efficiently for contact-rich manipulation. We propose a hierarchical optimization framework where Mixed-Integer Linear Program (MILP) selects optimal contacts between robot \& object using approximate dynamical constraints, and then a NonLinear Program (NLP) optimizes trajectory of the robot(s) and object considering full nonlinear constraints. We present a convex relaxation of bilinear constraints using binary encoding technique such that MILP can provide tighter solutions with better computational complexity. The proposed framework is evaluated on various manipulation tasks where it can reason about complex multi-contact interactions while providing computational advantages. We also demonstrate our framework in hardware experiments using a bimanual robot system.
Constrained Dynamic Movement Primitives for Safe Learning of Motor Skills
Sep 28, 2022
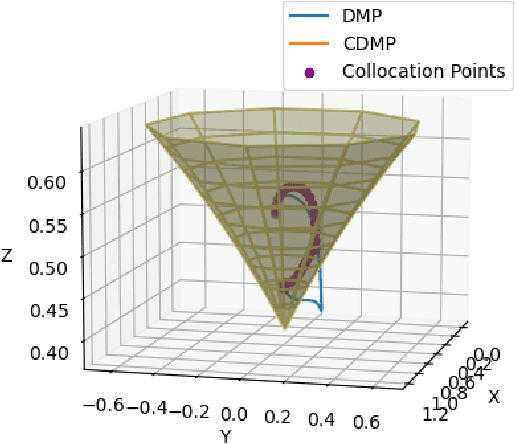
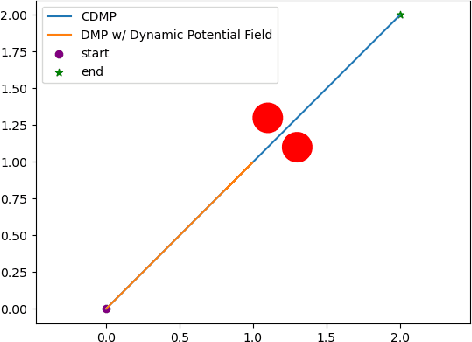
Abstract:Dynamic movement primitives are widely used for learning skills which can be demonstrated to a robot by a skilled human or controller. While their generalization capabilities and simple formulation make them very appealing to use, they possess no strong guarantees to satisfy operational safety constraints for a task. In this paper, we present constrained dynamic movement primitives (CDMP) which can allow for constraint satisfaction in the robot workspace. We present a formulation of a non-linear optimization to perturb the DMP forcing weights regressed by locally-weighted regression to admit a Zeroing Barrier Function (ZBF), which certifies workspace constraint satisfaction. We demonstrate the proposed CDMP under different constraints on the end-effector movement such as obstacle avoidance and workspace constraints on a physical robot. A video showing the implementation of the proposed algorithm using different manipulators in different environments could be found here https://youtu.be/hJegJJkJfys.
Transformer Networks for Predictive Group Elevator Control
Aug 15, 2022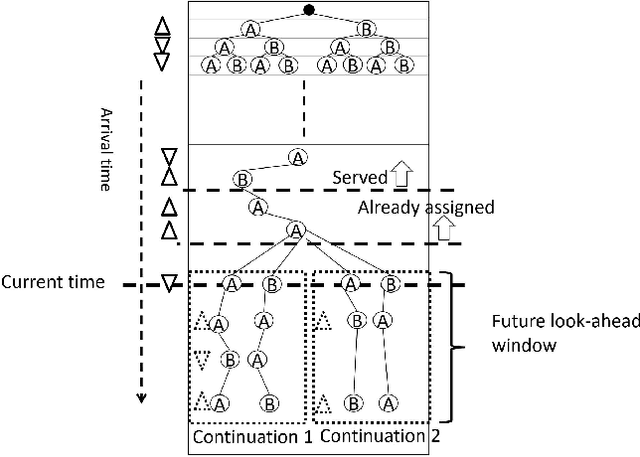
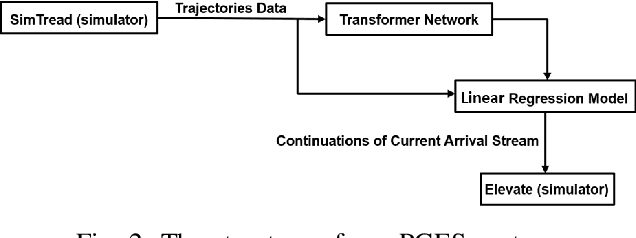
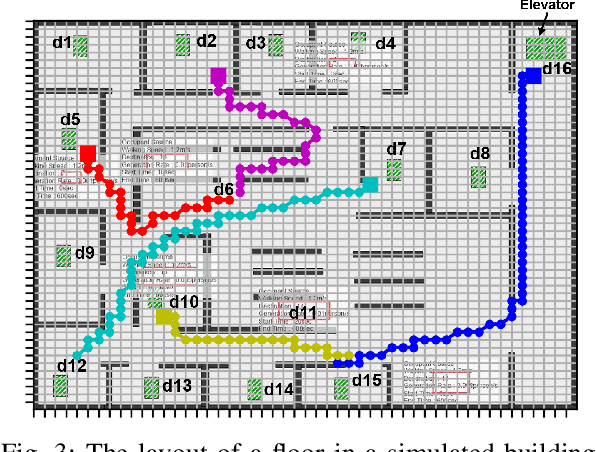
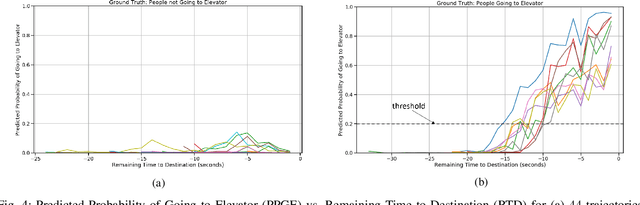
Abstract:We propose a Predictive Group Elevator Scheduler by using predictive information of passengers arrivals from a Transformer based destination predictor and a linear regression model that predicts remaining time to destinations. Through extensive empirical evaluation, we find that the savings of Average Waiting Time (AWT) could be as high as above 50% for light arrival streams and around 15% for medium arrival streams in afternoon down-peak traffic regimes. Such results can be obtained after carefully setting the Predicted Probability of Going to Elevator (PPGE) threshold, thus avoiding a majority of false predictions for people heading to the elevator, while achieving as high as 80% of true predictive elevator landings as early as after having seen only 60% of the whole trajectory of a passenger.
Robust Pivoting: Exploiting Frictional Stability Using Bilevel Optimization
Mar 22, 2022



Abstract:Generalizable manipulation requires that robots be able to interact with novel objects and environment. This requirement makes manipulation extremely challenging as a robot has to reason about complex frictional interaction with uncertainty in physical properties of the object. In this paper, we study robust optimization for control of pivoting manipulation in the presence of uncertainties. We present insights about how friction can be exploited to compensate for the inaccuracies in the estimates of the physical properties during manipulation. In particular, we derive analytical expressions for stability margin provided by friction during pivoting manipulation. This margin is then used in a bilevel trajectory optimization algorithm to design a controller that maximizes this stability margin to provide robustness against uncertainty in physical properties of the object. We demonstrate our proposed method using a 6 DoF manipulator for manipulating several different objects.
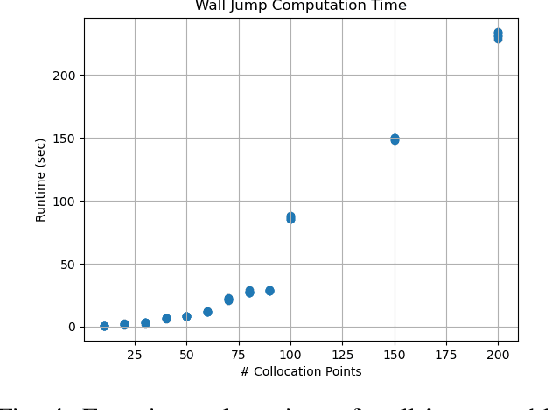
PYROBOCOP: Python-based Robotic Control & Optimization Package for Manipulation
Mar 18, 2022



Abstract:PYROBOCOP is a Python-based package for control, optimization and estimation of robotic systems described by nonlinear Differential Algebraic Equations (DAEs). In particular, the package can handle systems with contacts that are described by complementarity constraints and provides a general framework for specifying obstacle avoidance constraints. The package performs direct transcription of the DAEs into a set of nonlinear equations by performing orthogonal collocation on finite elements. PYROBOCOP provides automatic reformulation of the complementarity constraints that are tractable to NLP solvers to perform optimization of robotic systems. The package is interfaced with ADOL-C[1] for obtaining sparse derivatives by automatic differentiation and IPOPT[2] for performing optimization. We evaluate PYROBOCOP on several manipulation problems for control and estimation.
Chance-Constrained Optimization in Contact-Rich Systems for Robust Manipulation
Mar 05, 2022



Abstract:This paper presents a chance-constrained formulation for robust trajectory optimization during manipulation. In particular, we present a chance-constrained optimization for Stochastic Discrete-time Linear Complementarity Systems (SDLCS). To solve the optimization problem, we formulate Mixed-Integer Quadratic Programming with Chance Constraints (MIQPCC). In our formulation, we explicitly consider joint chance constraints for complementarity as well as states to capture the stochastic evolution of dynamics. We evaluate robustness of our optimized trajectories in simulation on several systems. The proposed approach outperforms some recent approaches for robust trajectory optimization for SDLCS.
* 9 pages, 9 figures
Quasi-Newton Trust Region Policy Optimization
Dec 26, 2019



Abstract:We propose a trust region method for policy optimization that employs Quasi-Newton approximation for the Hessian, called Quasi-Newton Trust Region Policy Optimization QNTRPO. Gradient descent is the de facto algorithm for reinforcement learning tasks with continuous controls. The algorithm has achieved state-of-the-art performance when used in reinforcement learning across a wide range of tasks. However, the algorithm suffers from a number of drawbacks including: lack of stepsize selection criterion, and slow convergence. We investigate the use of a trust region method using dogleg step and a Quasi-Newton approximation for the Hessian for policy optimization. We demonstrate through numerical experiments over a wide range of challenging continuous control tasks that our particular choice is efficient in terms of number of samples and improves performance
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge