Planning Shorter Paths in Graphs of Convex Sets by Undistorting Parametrized Configuration Spaces

Optimization based motion planning provides a useful modeling framework through various costs and constraints. Using Graph of Convex Sets (GCS) for trajectory optimization gives guarantees of feasibility and optimality by representing configuration space as the finite union of convex sets. Nonlinear parametrizations can be used to extend this technique to handle cases such as kinematic loops, but this distorts distances, such that solving with convex objectives will yield paths that are suboptimal in the original space. We present a method to extend GCS to nonconvex objectives, allowing us to "undistort" the optimization landscape while maintaining feasibility guarantees. We demonstrate our method's efficacy on three different robotic planning domains: a bimanual robot moving an object with both arms, the set of 3D rotations using Euler angles, and a rational parametrization of kinematics that enables certifying regions as collision free. Across the board, our method significantly improves path length and trajectory duration with only a minimal increase in runtime. Website: https://shrutigarg914.github.io/pgd-gcs-results/

Gemma 2: Improving Open Language Models at a Practical Size

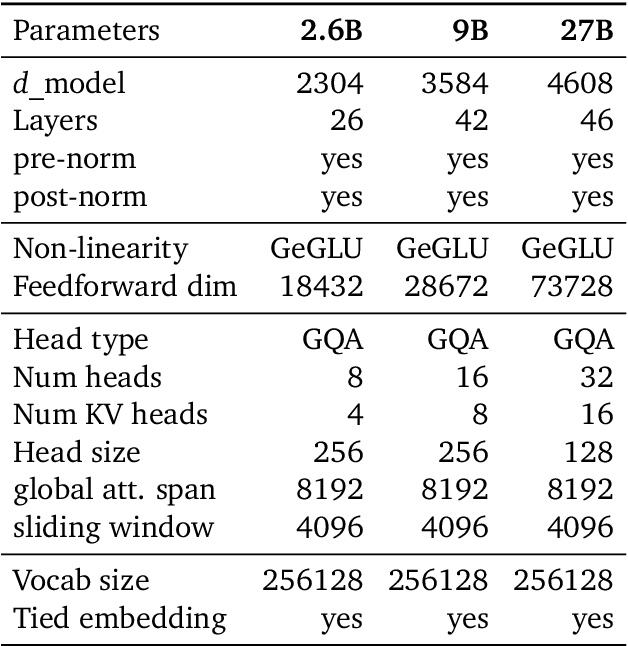
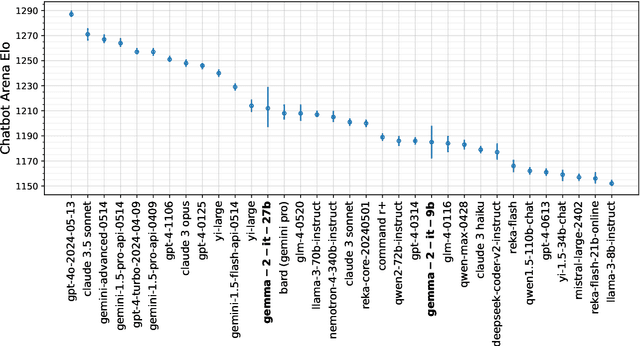
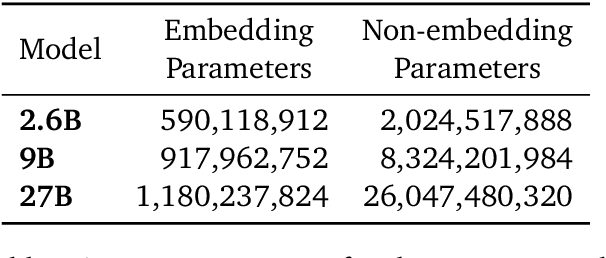
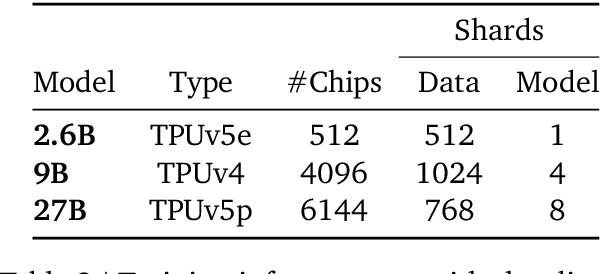
In this work, we introduce Gemma 2, a new addition to the Gemma family of lightweight, state-of-the-art open models, ranging in scale from 2 billion to 27 billion parameters. In this new version, we apply several known technical modifications to the Transformer architecture, such as interleaving local-global attentions (Beltagy et al., 2020a) and group-query attention (Ainslie et al., 2023). We also train the 2B and 9B models with knowledge distillation (Hinton et al., 2015) instead of next token prediction. The resulting models deliver the best performance for their size, and even offer competitive alternatives to models that are 2-3 times bigger. We release all our models to the community.