Multi-Query Shortest-Path Problem in Graphs of Convex Sets

The Shortest-Path Problem in Graph of Convex Sets (SPP in GCS) is a recently developed optimization framework that blends discrete and continuous decision making. Many relevant problems in robotics, such as collision-free motion planning, can be cast and solved as an SPP in GCS, yielding lower-cost solutions and faster runtimes than state-of-the-art algorithms. In this paper, we are motivated by motion planning of robot arms that must operate swiftly in static environments. We consider a multi-query extension of the SPP in GCS, where the goal is to efficiently precompute optimal paths between given sets of initial and target conditions. Our solution consists of two stages. Offline, we use semidefinite programming to compute a coarse lower bound on the problem's cost-to-go function. Then, online, this lower bound is used to incrementally generate feasible paths by solving short-horizon convex programs. For a robot arm with seven joints, our method designs higher quality trajectories up to two orders of magnitude faster than existing motion planners.

Towards Tight Convex Relaxations for Contact-Rich Manipulation

We present a method for global motion planning of robotic systems that interact with the environment through contacts. Our method directly handles the hybrid nature of such tasks using tools from convex optimization. We formulate the motion-planning problem as a shortest-path problem in a graph of convex sets, where a path in the graph corresponds to a contact sequence and a convex set models the quasi-static dynamics within a fixed contact mode. For each contact mode, we use semidefinite programming to relax the nonconvex dynamics that results from the simultaneous optimization of the object's pose, contact locations, and contact forces. The result is a tight convex relaxation of the overall planning problem, that can be efficiently solved and quickly rounded to find a feasible contact-rich trajectory. As a first application of this technique, we focus on the task of planar pushing. Exhaustive experiments show that our convex-optimization method generates plans that are consistently within a small percentage of the global optimum. We demonstrate the quality of these plans on a real robotic system.

Rapid and Reliable Trajectory Planning Involving Omnidirectional Jumping of Quadruped Robots

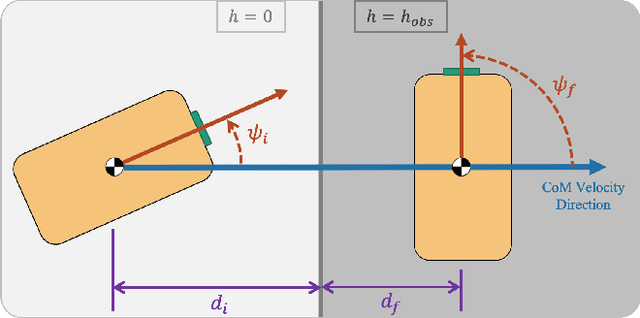
Dynamic jumping with multi-legged robots poses a challenging problem in planning and control. Formulating the jump optimization to allow fast online execution is difficult; efficiently using this capability to generate long-horizon trajectories further complicates the problem. In this work, we present a novel hierarchical planning framework to address this problem. We first formulate a real-time tractable trajectory optimization for performing omnidirectional jumping. We then embed the results of this optimization into a low dimensional jump feasibility classifier. This classifier is leveraged by a high-level planner to produce paths that are both dynamically feasible and also robust to variability in hardware trajectory realizations. We deploy our framework on the Mini Cheetah Vision quadruped, demonstrating robot's ability to generate and execute reliable, goal-oriented paths that involve forward, lateral, and rotational jumps onto surfaces 1.35 times taller than robot's nominal hip height. The ability to plan through omnidirectional jumping greatly expands robot's mobility relative to planners that restrict jumping to the sagittal or frontal planes.