SEEV: Synthesis with Efficient Exact Verification for ReLU Neural Barrier Functions

Neural Control Barrier Functions (NCBFs) have shown significant promise in enforcing safety constraints on nonlinear autonomous systems. State-of-the-art exact approaches to verifying safety of NCBF-based controllers exploit the piecewise-linear structure of ReLU neural networks, however, such approaches still rely on enumerating all of the activation regions of the network near the safety boundary, thus incurring high computation cost. In this paper, we propose a framework for Synthesis with Efficient Exact Verification (SEEV). Our framework consists of two components, namely (i) an NCBF synthesis algorithm that introduces a novel regularizer to reduce the number of activation regions at the safety boundary, and (ii) a verification algorithm that exploits tight over-approximations of the safety conditions to reduce the cost of verifying each piecewise-linear segment. Our simulations show that SEEV significantly improves verification efficiency while maintaining the CBF quality across various benchmark systems and neural network structures. Our code is available at https://github.com/HongchaoZhang-HZ/SEEV.

Verification and Synthesis of Compatible Control Lyapunov and Control Barrier Functions

Safety and stability are essential properties of control systems. Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs) have been proposed to ensure safety and stability respectively. However, previous approaches typically verify and synthesize the CBFs and CLFs separately, satisfying their respective constraints, without proving that the CBFs and CLFs are compatible with each other, namely at every state, there exists control actions that satisfy both the CBF and CLF constraints simultaneously. There exists some recent works that synthesized compatible CLF and CBF, but relying on nominal polynomial or rational controllers, which is just a sufficient but not necessary condition for compatibility. In this work, we investigate verification and synthesis of compatible CBF and CLF independent from any nominal controllers. We derive exact necessary and sufficient conditions for compatibility, and further formulate Sum-Of-Squares program for the compatibility verification. Based on our verification framework, we also design an alternating nominal-controller-free synthesis method. We evaluate our method in a linear toy, a non-linear toy, and a power converter example.

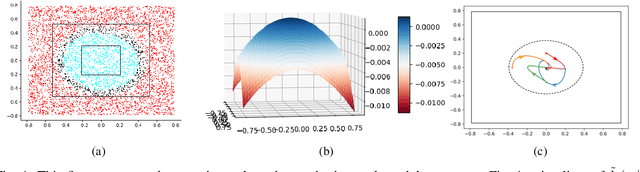
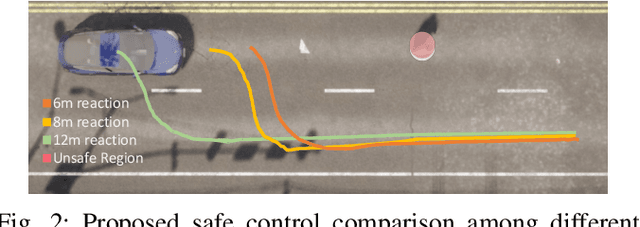
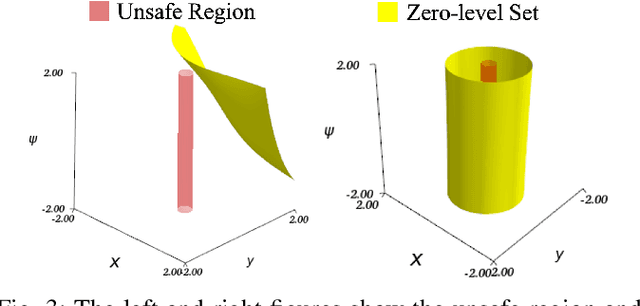
Learning a Formally Verified Control Barrier Function in Stochastic Environment

Safety is a fundamental requirement of control systems. Control Barrier Functions (CBFs) are proposed to ensure the safety of the control system by constructing safety filters or synthesizing control inputs. However, the safety guarantee and performance of safe controllers rely on the construction of valid CBFs. Inspired by universal approximatability, CBFs are represented by neural networks, known as neural CBFs (NCBFs). This paper presents an algorithm for synthesizing formally verified continuous-time neural Control Barrier Functions in stochastic environments in a single step. The proposed training process ensures efficacy across the entire state space with only a finite number of data points by constructing a sample-based learning framework for Stochastic Neural CBFs (SNCBFs). Our methodology eliminates the need for post hoc verification by enforcing Lipschitz bounds on the neural network, its Jacobian, and Hessian terms. We demonstrate the effectiveness of our approach through case studies on the inverted pendulum system and obstacle avoidance in autonomous driving, showcasing larger safe regions compared to baseline methods.

Fault Tolerant Neural Control Barrier Functions for Robotic Systems under Sensor Faults and Attacks

Safety is a fundamental requirement of many robotic systems. Control barrier function (CBF)-based approaches have been proposed to guarantee the safety of robotic systems. However, the effectiveness of these approaches highly relies on the choice of CBFs. Inspired by the universal approximation power of neural networks, there is a growing trend toward representing CBFs using neural networks, leading to the notion of neural CBFs (NCBFs). Current NCBFs, however, are trained and deployed in benign environments, making them ineffective for scenarios where robotic systems experience sensor faults and attacks. In this paper, we study safety-critical control synthesis for robotic systems under sensor faults and attacks. Our main contribution is the development and synthesis of a new class of CBFs that we term fault tolerant neural control barrier function (FT-NCBF). We derive the necessary and sufficient conditions for FT-NCBFs to guarantee safety, and develop a data-driven method to learn FT-NCBFs by minimizing a loss function constructed using the derived conditions. Using the learned FT-NCBF, we synthesize a control input and formally prove the safety guarantee provided by our approach. We demonstrate our proposed approach using two case studies: obstacle avoidance problem for an autonomous mobile robot and spacecraft rendezvous problem, with code available via https://github.com/HongchaoZhang-HZ/FTNCBF.

Exact Verification of ReLU Neural Control Barrier Functions

Control Barrier Functions (CBFs) are a popular approach for safe control of nonlinear systems. In CBF-based control, the desired safety properties of the system are mapped to nonnegativity of a CBF, and the control input is chosen to ensure that the CBF remains nonnegative for all time. Recently, machine learning methods that represent CBFs as neural networks (neural control barrier functions, or NCBFs) have shown great promise due to the universal representability of neural networks. However, verifying that a learned CBF guarantees safety remains a challenging research problem. This paper presents novel exact conditions and algorithms for verifying safety of feedforward NCBFs with ReLU activation functions. The key challenge in doing so is that, due to the piecewise linearity of the ReLU function, the NCBF will be nondifferentiable at certain points, thus invalidating traditional safety verification methods that assume a smooth barrier function. We resolve this issue by leveraging a generalization of Nagumo's theorem for proving invariance of sets with nonsmooth boundaries to derive necessary and sufficient conditions for safety. Based on this condition, we propose an algorithm for safety verification of NCBFs that first decomposes the NCBF into piecewise linear segments and then solves a nonlinear program to verify safety of each segment as well as the intersections of the linear segments. We mitigate the complexity by only considering the boundary of the safe region and by pruning the segments with Interval Bound Propagation (IBP) and linear relaxation. We evaluate our approach through numerical studies with comparison to state-of-the-art SMT-based methods. Our code is available at https://github.com/HongchaoZhang-HZ/exactverif-reluncbf-nips23.

Generalized Uniformly Optimal Methods for Nonlinear Programming

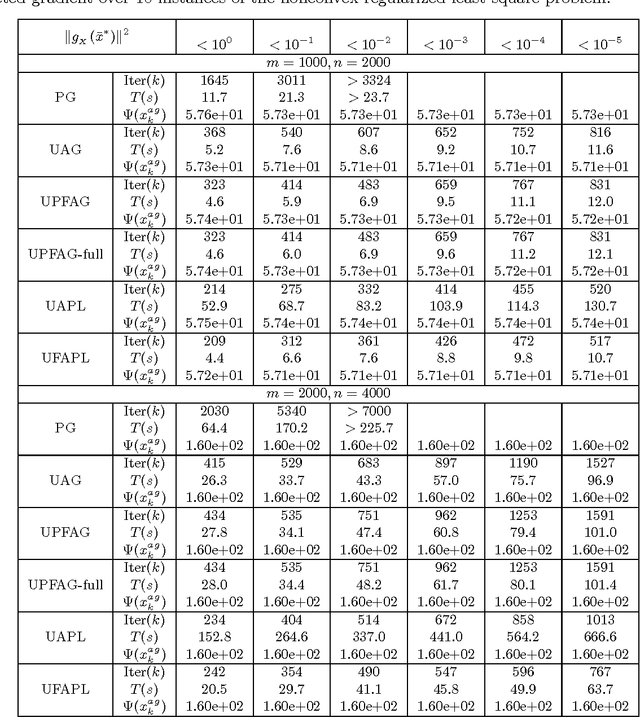
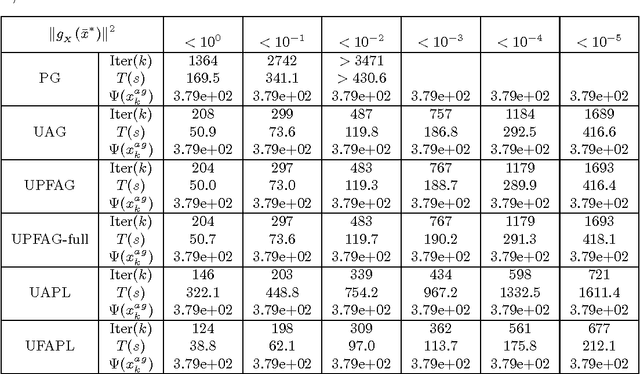
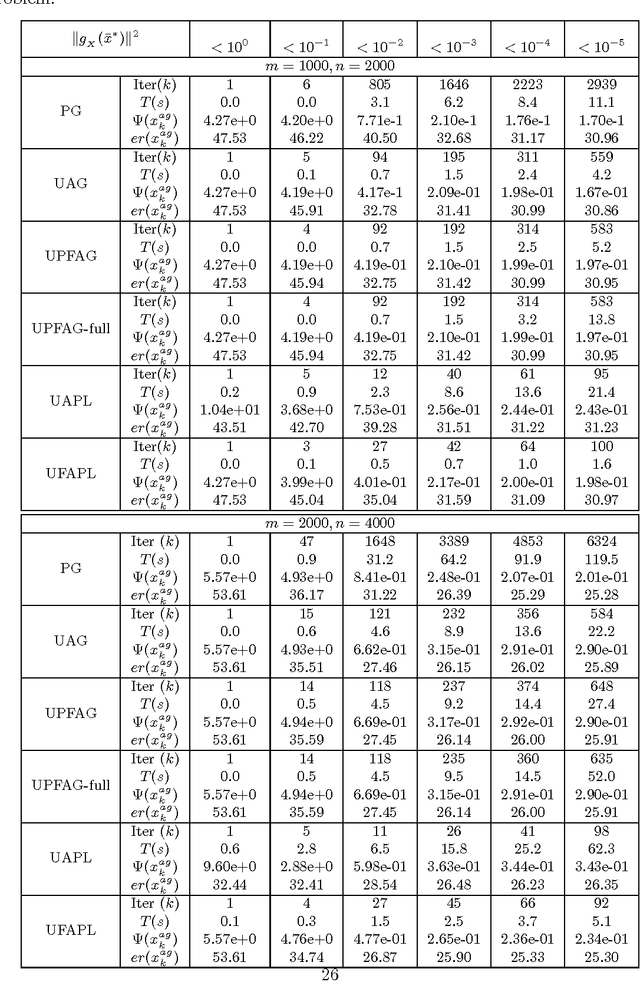
In this paper, we present a generic framework to extend existing uniformly optimal convex programming algorithms to solve more general nonlinear, possibly nonconvex, optimization problems. The basic idea is to incorporate a local search step (gradient descent or Quasi-Newton iteration) into these uniformly optimal convex programming methods, and then enforce a monotone decreasing property of the function values computed along the trajectory. Algorithms of these types will then achieve the best known complexity for nonconvex problems, and the optimal complexity for convex ones without requiring any problem parameters. As a consequence, we can have a unified treatment for a general class of nonlinear programming problems regardless of their convexity and smoothness level. In particular, we show that the accelerated gradient and level methods, both originally designed for solving convex optimization problems only, can be used for solving both convex and nonconvex problems uniformly. In a similar vein, we show that some well-studied techniques for nonlinear programming, e.g., Quasi-Newton iteration, can be embedded into optimal convex optimization algorithms to possibly further enhance their numerical performance. Our theoretical and algorithmic developments are complemented by some promising numerical results obtained for solving a few important nonconvex and nonlinear data analysis problems in the literature.