SEEV: Synthesis with Efficient Exact Verification for ReLU Neural Barrier Functions

Neural Control Barrier Functions (NCBFs) have shown significant promise in enforcing safety constraints on nonlinear autonomous systems. State-of-the-art exact approaches to verifying safety of NCBF-based controllers exploit the piecewise-linear structure of ReLU neural networks, however, such approaches still rely on enumerating all of the activation regions of the network near the safety boundary, thus incurring high computation cost. In this paper, we propose a framework for Synthesis with Efficient Exact Verification (SEEV). Our framework consists of two components, namely (i) an NCBF synthesis algorithm that introduces a novel regularizer to reduce the number of activation regions at the safety boundary, and (ii) a verification algorithm that exploits tight over-approximations of the safety conditions to reduce the cost of verifying each piecewise-linear segment. Our simulations show that SEEV significantly improves verification efficiency while maintaining the CBF quality across various benchmark systems and neural network structures. Our code is available at https://github.com/HongchaoZhang-HZ/SEEV.

Verification and Synthesis of Compatible Control Lyapunov and Control Barrier Functions

Safety and stability are essential properties of control systems. Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs) have been proposed to ensure safety and stability respectively. However, previous approaches typically verify and synthesize the CBFs and CLFs separately, satisfying their respective constraints, without proving that the CBFs and CLFs are compatible with each other, namely at every state, there exists control actions that satisfy both the CBF and CLF constraints simultaneously. There exists some recent works that synthesized compatible CLF and CBF, but relying on nominal polynomial or rational controllers, which is just a sufficient but not necessary condition for compatibility. In this work, we investigate verification and synthesis of compatible CBF and CLF independent from any nominal controllers. We derive exact necessary and sufficient conditions for compatibility, and further formulate Sum-Of-Squares program for the compatibility verification. Based on our verification framework, we also design an alternating nominal-controller-free synthesis method. We evaluate our method in a linear toy, a non-linear toy, and a power converter example.

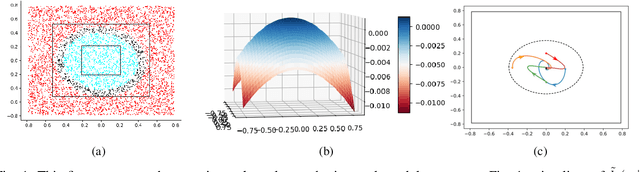
Learning a Formally Verified Control Barrier Function in Stochastic Environment

Safety is a fundamental requirement of control systems. Control Barrier Functions (CBFs) are proposed to ensure the safety of the control system by constructing safety filters or synthesizing control inputs. However, the safety guarantee and performance of safe controllers rely on the construction of valid CBFs. Inspired by universal approximatability, CBFs are represented by neural networks, known as neural CBFs (NCBFs). This paper presents an algorithm for synthesizing formally verified continuous-time neural Control Barrier Functions in stochastic environments in a single step. The proposed training process ensures efficacy across the entire state space with only a finite number of data points by constructing a sample-based learning framework for Stochastic Neural CBFs (SNCBFs). Our methodology eliminates the need for post hoc verification by enforcing Lipschitz bounds on the neural network, its Jacobian, and Hessian terms. We demonstrate the effectiveness of our approach through case studies on the inverted pendulum system and obstacle avoidance in autonomous driving, showcasing larger safe regions compared to baseline methods.

Fault Tolerant Neural Control Barrier Functions for Robotic Systems under Sensor Faults and Attacks

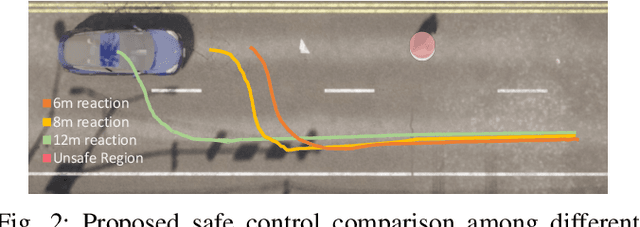
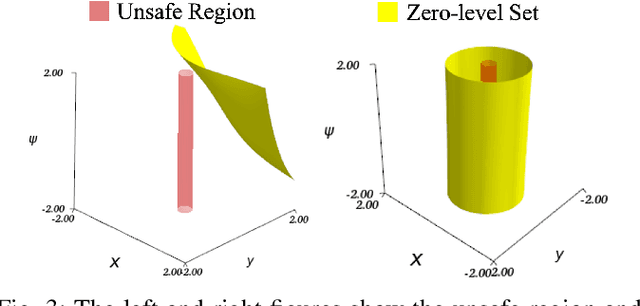
Safety is a fundamental requirement of many robotic systems. Control barrier function (CBF)-based approaches have been proposed to guarantee the safety of robotic systems. However, the effectiveness of these approaches highly relies on the choice of CBFs. Inspired by the universal approximation power of neural networks, there is a growing trend toward representing CBFs using neural networks, leading to the notion of neural CBFs (NCBFs). Current NCBFs, however, are trained and deployed in benign environments, making them ineffective for scenarios where robotic systems experience sensor faults and attacks. In this paper, we study safety-critical control synthesis for robotic systems under sensor faults and attacks. Our main contribution is the development and synthesis of a new class of CBFs that we term fault tolerant neural control barrier function (FT-NCBF). We derive the necessary and sufficient conditions for FT-NCBFs to guarantee safety, and develop a data-driven method to learn FT-NCBFs by minimizing a loss function constructed using the derived conditions. Using the learned FT-NCBF, we synthesize a control input and formally prove the safety guarantee provided by our approach. We demonstrate our proposed approach using two case studies: obstacle avoidance problem for an autonomous mobile robot and spacecraft rendezvous problem, with code available via https://github.com/HongchaoZhang-HZ/FTNCBF.

Almost-Sure Safety Guarantees of Stochastic Zero-Control Barrier Functions Do Not Hold

The 2021 paper "Control barrier functions for stochastic systems" provides theorems that give almost sure safety guarantees given stochastic zero control barrier function (ZCBF). Unfortunately, both the theorem and its proof is invalid. In this letter, we illustrate on a toy example that the almost sure safety guarantees for stochastic ZCBF do not hold and explain why the proof is flawed. Although stochastic reciprocal barrier functions (RCBF) also uses the same proof technique, we provide a different proof technique that verifies that stochastic RCBFs are indeed safe with probability one. Using the RCBF, we derive a modified ZCBF condition that guarantees safety with probability one. Finally, we provide some discussion on the role of unbounded controls in the almost-sure safety guarantees of RCBFs, and show that the rate of divergence of the ratio of the drift and diffusion is the key for whether a system has almost sure safety guarantees.

Exact Verification of ReLU Neural Control Barrier Functions

Control Barrier Functions (CBFs) are a popular approach for safe control of nonlinear systems. In CBF-based control, the desired safety properties of the system are mapped to nonnegativity of a CBF, and the control input is chosen to ensure that the CBF remains nonnegative for all time. Recently, machine learning methods that represent CBFs as neural networks (neural control barrier functions, or NCBFs) have shown great promise due to the universal representability of neural networks. However, verifying that a learned CBF guarantees safety remains a challenging research problem. This paper presents novel exact conditions and algorithms for verifying safety of feedforward NCBFs with ReLU activation functions. The key challenge in doing so is that, due to the piecewise linearity of the ReLU function, the NCBF will be nondifferentiable at certain points, thus invalidating traditional safety verification methods that assume a smooth barrier function. We resolve this issue by leveraging a generalization of Nagumo's theorem for proving invariance of sets with nonsmooth boundaries to derive necessary and sufficient conditions for safety. Based on this condition, we propose an algorithm for safety verification of NCBFs that first decomposes the NCBF into piecewise linear segments and then solves a nonlinear program to verify safety of each segment as well as the intersections of the linear segments. We mitigate the complexity by only considering the boundary of the safe region and by pruning the segments with Interval Bound Propagation (IBP) and linear relaxation. We evaluate our approach through numerical studies with comparison to state-of-the-art SMT-based methods. Our code is available at https://github.com/HongchaoZhang-HZ/exactverif-reluncbf-nips23.

Neural Lyapunov Control for Discrete-Time Systems

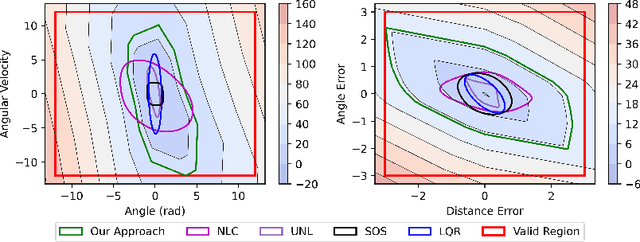
While ensuring stability for linear systems is well understood, it remains a major challenge for systems with nonlinear dynamics. A general approach in such cases is to leverage Lyapunov stability theory to compute a combination of a Lyapunov control function and an associated control policy. However, finding Lyapunov functions for general nonlinear systems is a challenging task. To address this challenge, several methods have been recently proposed that represent Lyapunov functions using neural networks. However, such approaches have been designed exclusively for continuous-time systems. We propose the first approach for learning neural Lyapunov control in discrete-time systems. Three key ingredients enable us to effectively learn provably stable control policies. The first is a novel mixed-integer linear programming approach for verifying the stability conditions in discrete-time systems. The second is a novel approach for computing sub-level sets which characterize the region of attraction. Finally, we rely on a heuristic gradient-based approach for quickly finding counterexamples to significantly speed up Lyapunov function learning. Our experiments on four standard benchmarks demonstrate that our approach significantly outperforms state-of-the-art baselines. For example, on the path tracking benchmark, we outperform recent neural Lyapunov control baselines by an order of magnitude in both running time and the size of the region of attraction, and on two of the four benchmarks (cartpole and PVTOL), ours is the first automated approach to return a provably stable controller.

Pre-processing training data improves accuracy and generalisability of convolutional neural network based landscape semantic segmentation

In this paper, we trialled different methods of data preparation for Convolutional Neural Network (CNN) training and semantic segmentation of land use land cover (LULC) features within aerial photography over the Wet Tropics and Atherton Tablelands, Queensland, Australia. This was conducted through trialling and ranking various training patch selection sampling strategies, patch and batch sizes and data augmentations and scaling. We also compared model accuracy through producing the LULC classification using a single pass of a grid of patches and averaging multiple grid passes and three rotated version of each patch. Our results showed: a stratified random sampling approach for producing training patches improved the accuracy of classes with a smaller area while having minimal effect on larger classes; a smaller number of larger patches compared to a larger number of smaller patches improves model accuracy; applying data augmentations and scaling are imperative in creating a generalised model able to accurately classify LULC features in imagery from a different date and sensor; and producing the output classification by averaging multiple grids of patches and three rotated versions of each patch produced and more accurate and aesthetic result. Combining the findings from the trials, we fully trained five models on the 2018 training image and applied the model to the 2015 test image with the output LULC classifications achieving an average kappa of 0.84 user accuracy of 0.81 and producer accuracy of 0.87. This study has demonstrated the importance of data pre-processing for developing a generalised deep-learning model for LULC classification which can be applied to a different date and sensor. Future research using CNN and earth observation data should implement the findings of this study to increase LULC model accuracy and transferability.

Risk-Aware Distributed Multi-Agent Reinforcement Learning

Autonomous cyber and cyber-physical systems need to perform decision-making, learning, and control in unknown environments. Such decision-making can be sensitive to multiple factors, including modeling errors, changes in costs, and impacts of events in the tails of probability distributions. Although multi-agent reinforcement learning (MARL) provides a framework for learning behaviors through repeated interactions with the environment by minimizing an average cost, it will not be adequate to overcome the above challenges. In this paper, we develop a distributed MARL approach to solve decision-making problems in unknown environments by learning risk-aware actions. We use the conditional value-at-risk (CVaR) to characterize the cost function that is being minimized, and define a Bellman operator to characterize the value function associated to a given state-action pair. We prove that this operator satisfies a contraction property, and that it converges to the optimal value function. We then propose a distributed MARL algorithm called the CVaR QD-Learning algorithm, and establish that value functions of individual agents reaches consensus. We identify several challenges that arise in the implementation of the CVaR QD-Learning algorithm, and present solutions to overcome these. We evaluate the CVaR QD-Learning algorithm through simulations, and demonstrate the effect of a risk parameter on value functions at consensus.

A Hybrid Submodular Optimization Approach to Controlled Islanding with Post-Disturbance Stability Guarantees

Disturbances may create cascading failures in power systems and lead to widespread blackouts. Controlled islanding is an effective approach to mitigate cascading failures by partitioning the power system into a set of disjoint islands. To retain the stability of the power system following disturbances, the islanding strategy should not only be minimally disruptive, but also guarantee post-disturbance stability. In this paper, we study the problem of synthesizing post-disturbance stability-aware controlled islanding strategies. To ensure post-disturbance stability, our computation of islanding strategies takes load-generation balance and transmission line capacity constraints into consideration, leading to a hybrid optimization problem with both discrete and continuous variables. To mitigate the computational challenge incurred when solving the hybrid optimization program, we propose the concepts of hybrid submodularity and hybrid matroid. We show that the islanding problem is equivalent to a hybrid matroid optimization program, whose objective function is hybrid supermodular. Leveraging the supermodularity property, we develop an efficient local search algorithm and show that the proposed algorithm achieves 1/2-optimality guarantee. We compare our approach with a baseline using mixed-integer linear program on IEEE 118-bus, IEEE 300-bus, ActivSg 500-bus, and Polish 2383-bus systems. Our results show that our approach outperforms the baseline in terms of the total cost incurred during islanding across all test cases. Furthermore, our proposed approach can find an islanding strategy for large-scale test cases such as Polish 2383-bus system, whereas the baseline approach becomes intractable.