Learning a Formally Verified Control Barrier Function in Stochastic Environment
Paper and Code
Mar 28, 2024
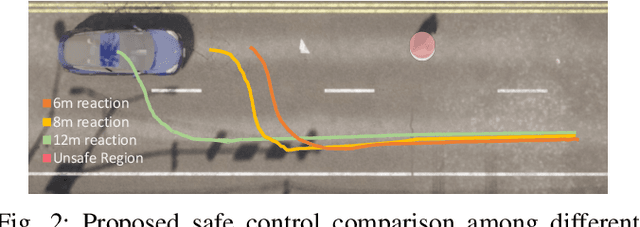
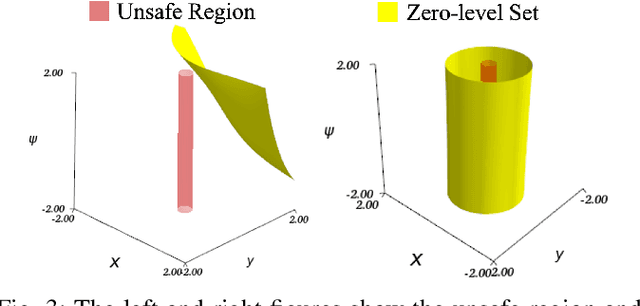
Safety is a fundamental requirement of control systems. Control Barrier Functions (CBFs) are proposed to ensure the safety of the control system by constructing safety filters or synthesizing control inputs. However, the safety guarantee and performance of safe controllers rely on the construction of valid CBFs. Inspired by universal approximatability, CBFs are represented by neural networks, known as neural CBFs (NCBFs). This paper presents an algorithm for synthesizing formally verified continuous-time neural Control Barrier Functions in stochastic environments in a single step. The proposed training process ensures efficacy across the entire state space with only a finite number of data points by constructing a sample-based learning framework for Stochastic Neural CBFs (SNCBFs). Our methodology eliminates the need for post hoc verification by enforcing Lipschitz bounds on the neural network, its Jacobian, and Hessian terms. We demonstrate the effectiveness of our approach through case studies on the inverted pendulum system and obstacle avoidance in autonomous driving, showcasing larger safe regions compared to baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge