Manan Tayal
Neural Control Barrier Functions from Physics Informed Neural Networks
Apr 15, 2025Abstract:As autonomous systems become increasingly prevalent in daily life, ensuring their safety is paramount. Control Barrier Functions (CBFs) have emerged as an effective tool for guaranteeing safety; however, manually designing them for specific applications remains a significant challenge. With the advent of deep learning techniques, recent research has explored synthesizing CBFs using neural networks-commonly referred to as neural CBFs. This paper introduces a novel class of neural CBFs that leverages a physics-inspired neural network framework by incorporating Zubov's Partial Differential Equation (PDE) within the context of safety. This approach provides a scalable methodology for synthesizing neural CBFs applicable to high-dimensional systems. Furthermore, by utilizing reciprocal CBFs instead of zeroing CBFs, the proposed framework allows for the specification of flexible, user-defined safe regions. To validate the effectiveness of the approach, we present case studies on three different systems: an inverted pendulum, autonomous ground navigation, and aerial navigation in obstacle-laden environments.
GenOSIL: Generalized Optimal and Safe Robot Control using Parameter-Conditioned Imitation Learning
Mar 15, 2025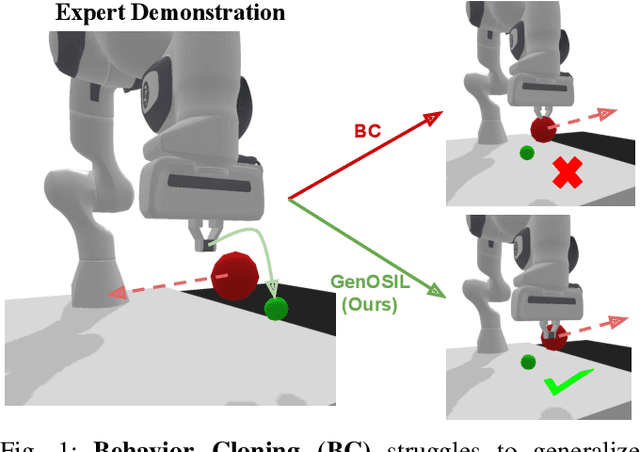
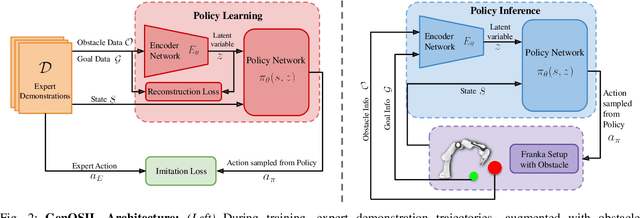
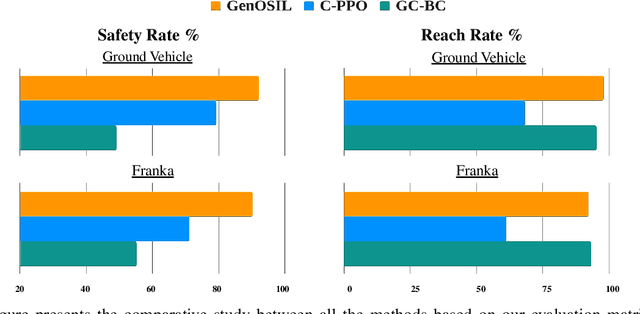
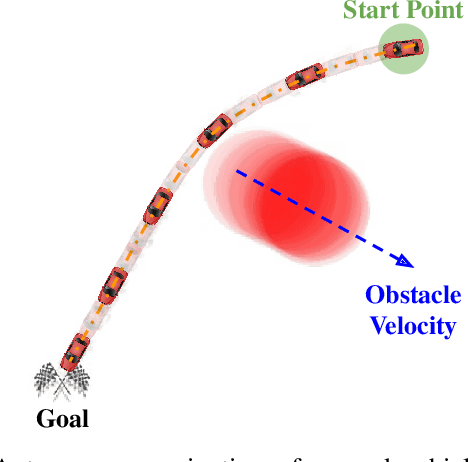
Abstract:Ensuring safe and generalizable control remains a fundamental challenge in robotics, particularly when deploying imitation learning in dynamic environments. Traditional behavior cloning (BC) struggles to generalize beyond its training distribution, as it lacks an understanding of the safety critical reasoning behind expert demonstrations. To address this limitation, we propose GenOSIL, a novel imitation learning framework that explicitly incorporates environment parameters into policy learning via a structured latent representation. Unlike conventional methods that treat the environment as a black box, GenOSIL employs a variational autoencoder (VAE) to encode measurable safety parameters such as obstacle position, velocity, and geometry into a latent space that captures intrinsic correlations between expert behavior and environmental constraints. This enables the policy to infer the rationale behind expert trajectories rather than merely replicating them. We validate our approach on two robotic platforms an autonomous ground vehicle and a Franka Emika Panda manipulator demonstrating superior safety and goal reaching performance compared to baseline methods. The simulation and hardware videos can be viewed on the project webpage: https://mumukshtayal.github.io/GenOSIL/.
Real Time Safety of Fixed-wing UAVs using Collision Cone Control Barrier Functions
Jul 27, 2024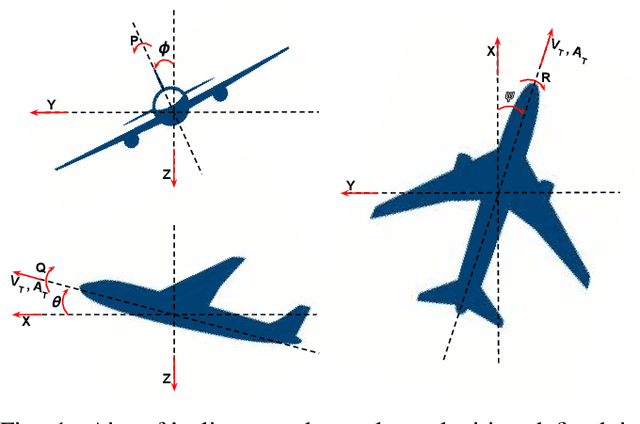
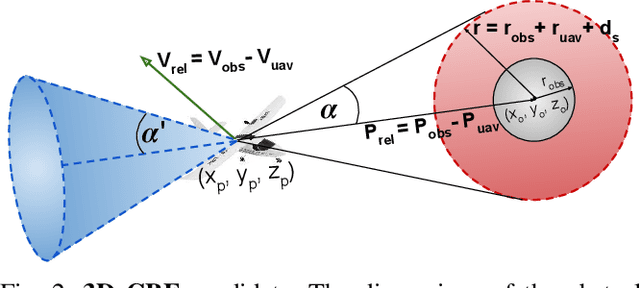
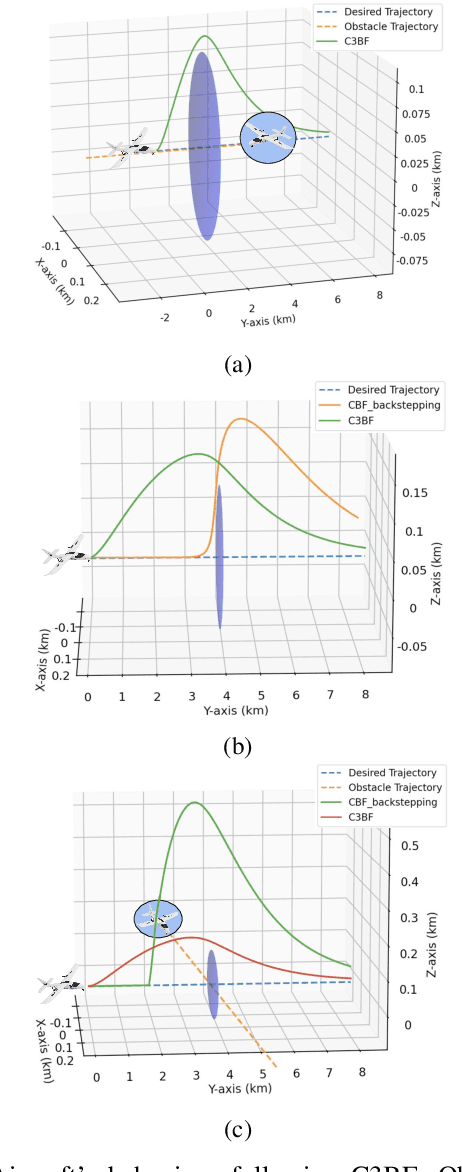
Abstract:Fixed-wing UAVs have transformed the transportation system with their high flight speed and long endurance, yet their safe operation in increasingly cluttered environments depends heavily on effective collision avoidance techniques. This paper presents a novel method for safely navigating an aircraft along a desired route while avoiding moving obstacles. We utilize a class of control barrier functions (CBFs) based on collision cones to ensure the relative velocity between the aircraft and the obstacle consistently avoids a cone of vectors that might lead to a collision. By demonstrating that the proposed constraint is a valid CBF for the aircraft, we can leverage its real-time implementation via Quadratic Programs (QPs), termed the CBF-QPs. Validation includes simulating control law along trajectories, showing effectiveness in both static and moving obstacle scenarios.
BiRoDiff: Diffusion policies for bipedal robot locomotion on unseen terrains
Jul 07, 2024Abstract:Locomotion on unknown terrains is essential for bipedal robots to handle novel real-world challenges, thus expanding their utility in disaster response and exploration. In this work, we introduce a lightweight framework that learns a single walking controller that yields locomotion on multiple terrains. We have designed a real-time robot controller based on diffusion models, which not only captures multiple behaviours with different velocities in a single policy but also generalizes well for unseen terrains. Our controller learns with offline data, which is better than online learning in aspects like scalability, simplicity in training scheme etc. We have designed and implemented a diffusion model-based policy controller in simulation on our custom-made Bipedal Robot model named Stoch BiRo. We have demonstrated its generalization capability and high frequency control step generation relative to typical generative models, which require huge onboarding compute.
Learning a Formally Verified Control Barrier Function in Stochastic Environment
Mar 28, 2024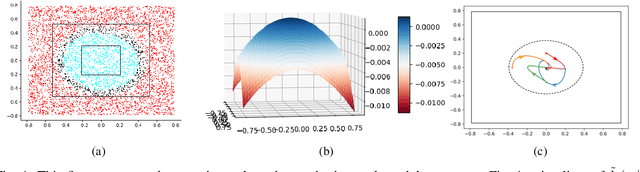
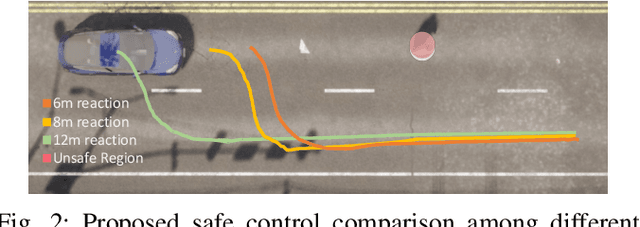
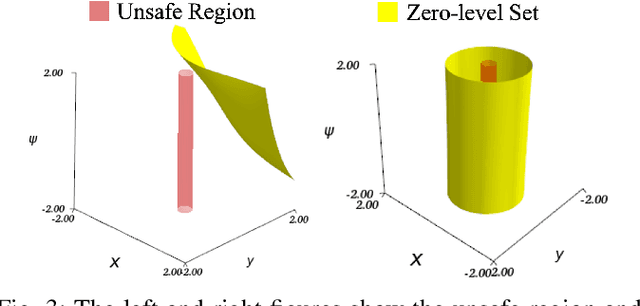
Abstract:Safety is a fundamental requirement of control systems. Control Barrier Functions (CBFs) are proposed to ensure the safety of the control system by constructing safety filters or synthesizing control inputs. However, the safety guarantee and performance of safe controllers rely on the construction of valid CBFs. Inspired by universal approximatability, CBFs are represented by neural networks, known as neural CBFs (NCBFs). This paper presents an algorithm for synthesizing formally verified continuous-time neural Control Barrier Functions in stochastic environments in a single step. The proposed training process ensures efficacy across the entire state space with only a finite number of data points by constructing a sample-based learning framework for Stochastic Neural CBFs (SNCBFs). Our methodology eliminates the need for post hoc verification by enforcing Lipschitz bounds on the neural network, its Jacobian, and Hessian terms. We demonstrate the effectiveness of our approach through case studies on the inverted pendulum system and obstacle avoidance in autonomous driving, showcasing larger safe regions compared to baseline methods.
A Collision Cone Approach for Control Barrier Functions
Mar 11, 2024
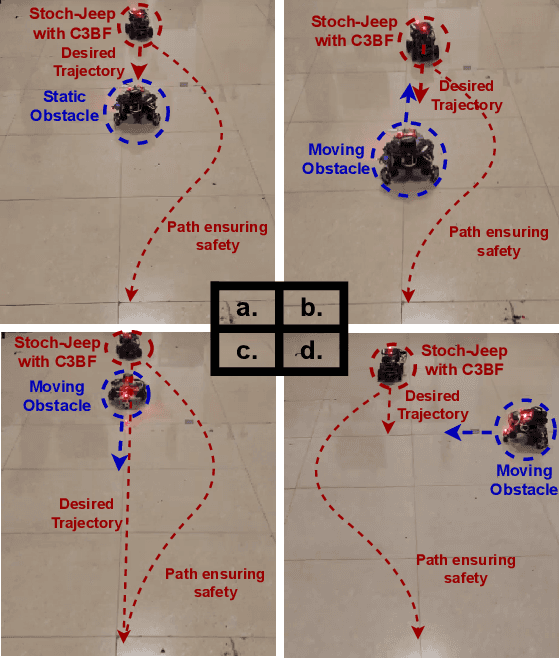
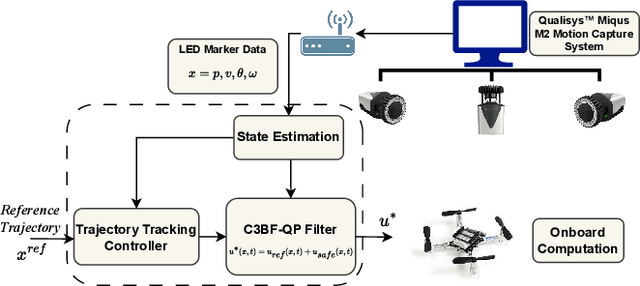
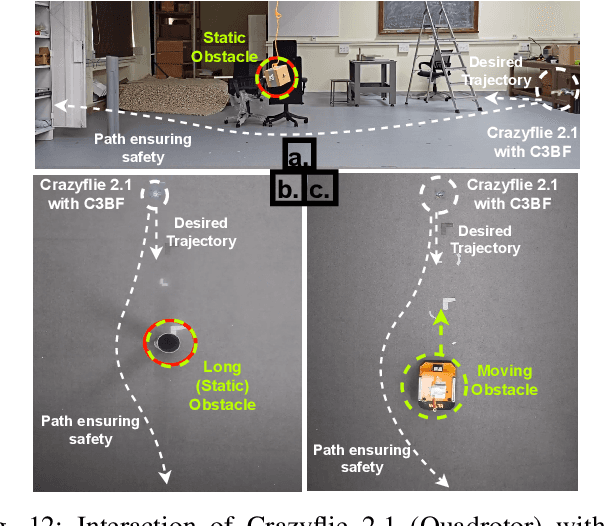
Abstract:This work presents a unified approach for collision avoidance using Collision-Cone Control Barrier Functions (CBFs) in both ground (UGV) and aerial (UAV) unmanned vehicles. We propose a novel CBF formulation inspired by collision cones, to ensure safety by constraining the relative velocity between the vehicle and the obstacle to always point away from each other. The efficacy of this approach is demonstrated through simulations and hardware implementations on the TurtleBot, Stoch-Jeep, and Crazyflie 2.1 quadrotor robot, showcasing its effectiveness in avoiding collisions with dynamic obstacles in both ground and aerial settings. The real-time controller is developed using CBF Quadratic Programs (CBF-QPs). Comparative analysis with the state-of-the-art CBFs highlights the less conservative nature of the proposed approach. Overall, this research contributes to a novel control formation that can give a guarantee for collision avoidance in unmanned vehicles by modifying the control inputs from existing path-planning controllers.
Stoch BiRo: Design and Control of a low cost bipedal robot
Dec 11, 2023Abstract:This paper introduces the Stoch BiRo, a cost-effective bipedal robot designed with a modular mechanical structure having point feet to navigate uneven and unfamiliar terrains. The robot employs proprioceptive actuation in abduction, hips, and knees, leveraging a Raspberry Pi4 for control. Overcoming computational limitations, a Learning-based Linear Policy controller manages balance and locomotion with only 3 degrees of freedom (DoF) per leg, distinct from the typical 5DoF in bipedal systems. Integrated within a modular control architecture, these controllers enable autonomous handling of unforeseen terrain disturbances without external sensors or prior environment knowledge. The robot's policies are trained and simulated using MuJoCo, transferring learned behaviors to the Stoch BiRo hardware for initial walking validations. This work highlights the Stoch BiRo's adaptability and cost-effectiveness in mechanical design, control strategies, and autonomous navigation, promising diverse applications in real-world robotics scenarios.
Polygonal Cone Control Barrier Functions (PolyC2BF) for safe navigation in cluttered environments
Nov 15, 2023Abstract:In fields such as mining, search and rescue, and archaeological exploration, ensuring real-time, collision-free navigation of robots in confined, cluttered environments is imperative. Despite the value of established path planning algorithms, they often face challenges in convergence rates and handling dynamic infeasibilities. Alternative techniques like collision cones struggle to accurately represent complex obstacle geometries. This paper introduces a novel category of control barrier functions, known as Polygonal Cone Control Barrier Function (PolyC2BF), which addresses overestimation and computational complexity issues. The proposed PolyC2BF, formulated as a Quadratic Programming (QP) problem, proves effective in facilitating collision-free movement of multiple robots in complex environments. The efficacy of this approach is further demonstrated through PyBullet simulations on quadruped (unicycle model), and crazyflie 2.1 (quadrotor model) in cluttered environments.
Collision Cone Control Barrier Functions: Experimental Validation on UGVs for Kinematic Obstacle Avoidance
Oct 16, 2023
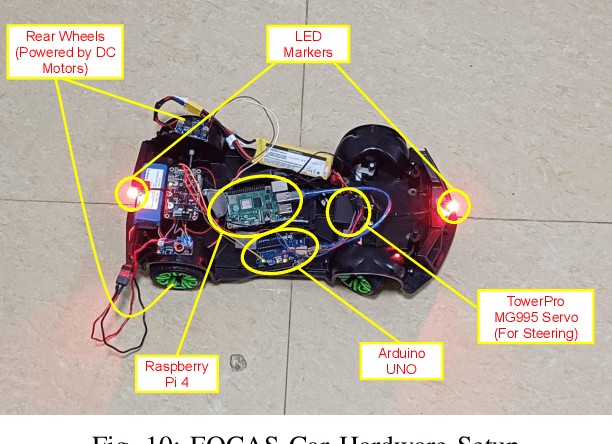
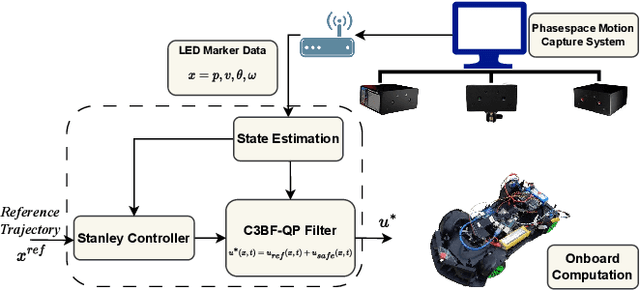
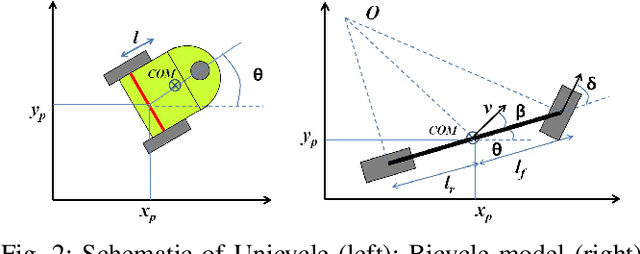
Abstract:Autonomy advances have enabled robots in diverse environments and close human interaction, necessitating controllers with formal safety guarantees. This paper introduces an experimental platform designed for the validation and demonstration of a novel class of Control Barrier Functions (CBFs) tailored for Unmanned Ground Vehicles (UGVs) to proactively prevent collisions with kinematic obstacles by integrating the concept of collision cones. While existing CBF formulations excel with static obstacles, extensions to torque/acceleration-controlled unicycle and bicycle models have seen limited success. Conventional CBF applications in nonholonomic UGV models have demonstrated control conservatism, particularly in scenarios where steering/thrust control was deemed infeasible. Drawing inspiration from collision cones in path planning, we present a pioneering CBF formulation ensuring theoretical safety guarantees for both unicycle and bicycle models. The core premise revolves around aligning the obstacle's velocity away from the vehicle, establishing a constraint to perpetually avoid vectors directed towards it. This control methodology is rigorously validated through simulations and experimental verification on the Copernicus mobile robot (Unicycle Model) and FOCAS-Car (Bicycle Model).
Convergence of ADAM with Constant Step Size in Non-Convex Settings: A Simple Proof
Sep 24, 2023Abstract:In neural network training, RMSProp and ADAM remain widely favoured optimization algorithms. One of the keys to their performance lies in selecting the correct step size, which can significantly influence their effectiveness. It is worth noting that these algorithms performance can vary considerably, depending on the chosen step sizes. Additionally, questions about their theoretical convergence properties continue to be a subject of interest. In this paper, we theoretically analyze a constant stepsize version of ADAM in the non-convex setting. We show sufficient conditions for the stepsize to achieve almost sure asymptotic convergence of the gradients to zero with minimal assumptions. We also provide runtime bounds for deterministic ADAM to reach approximate criticality when working with smooth, non-convex functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge