Deep Robust Koopman Learning from Noisy Data

Koopman operator theory has emerged as a leading data-driven approach that relies on a judicious choice of observable functions to realize global linear representations of nonlinear systems in the lifted observable space. However, real-world data is often noisy, making it difficult to obtain an accurate and unbiased approximation of the Koopman operator. The Koopman operator generated from noisy datasets is typically corrupted by noise-induced bias that severely degrades prediction and downstream tracking performance. In order to address this drawback, this paper proposes a novel autoencoder-based neural architecture to jointly learn the appropriate lifting functions and the reduced-bias Koopman operator from noisy data. The architecture initially learns the Koopman basis functions that are consistent for both the forward and backward temporal dynamics of the system. Subsequently, by utilizing the learned forward and backward temporal dynamics, the Koopman operator is synthesized with a reduced bias making the method more robust to noise compared to existing techniques. Theoretical analysis is used to demonstrate significant bias reduction in the presence of training noise. Dynamics prediction and tracking control simulations are conducted for multiple serial manipulator arms, including performance comparisons with leading alternative designs, to demonstrate its robustness under various noise levels. Experimental studies with the Franka FR3 7-DoF manipulator arm are further used to demonstrate the effectiveness of the proposed approach in a practical setting.

Adaptive Koopman Embedding for Robust Control of Complex Dynamical Systems

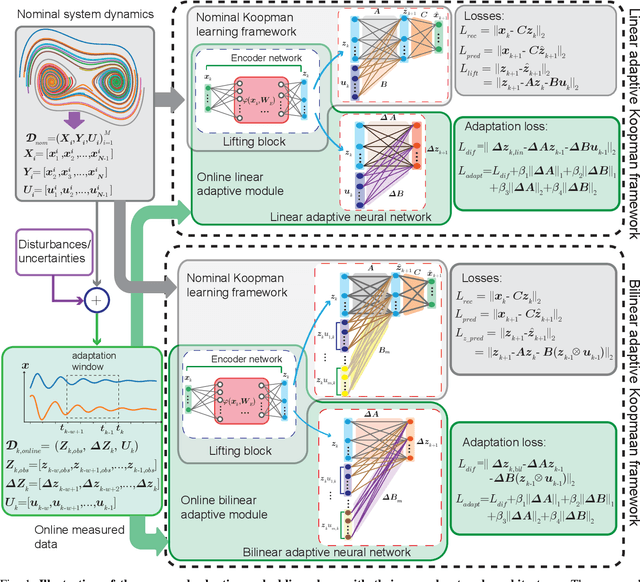
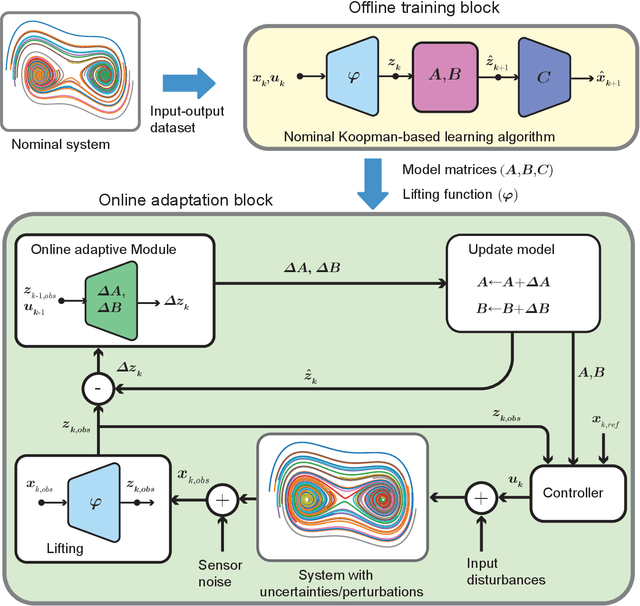
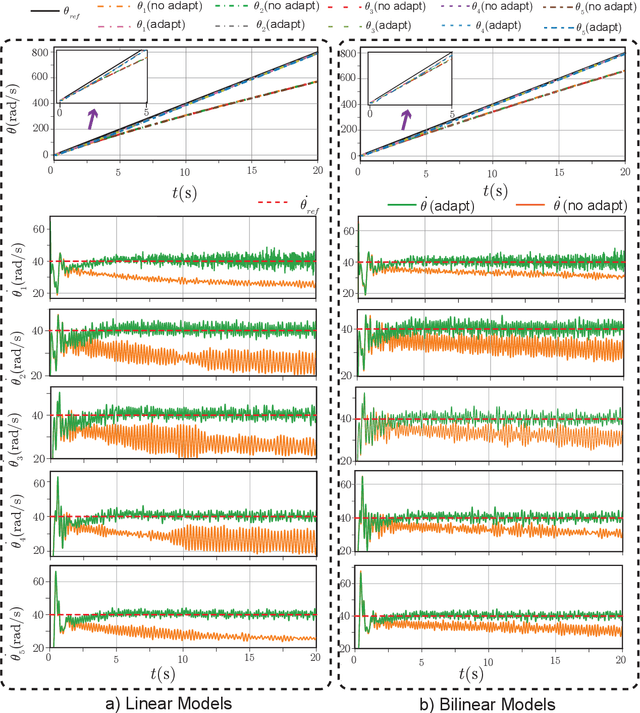
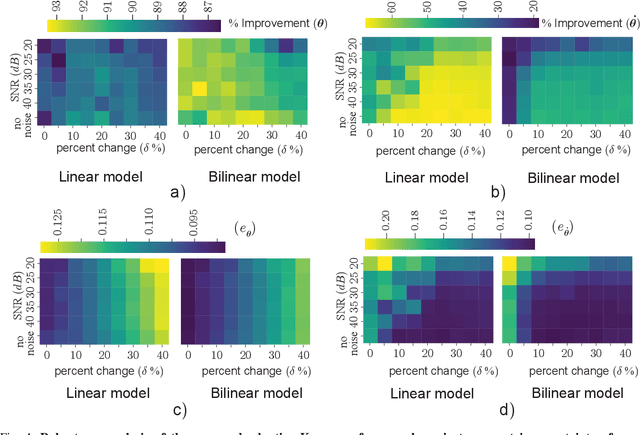
The discovery of linear embedding is the key to the synthesis of linear control techniques for nonlinear systems. In recent years, while Koopman operator theory has become a prominent approach for learning these linear embeddings through data-driven methods, these algorithms often exhibit limitations in generalizability beyond the distribution captured by training data and are not robust to changes in the nominal system dynamics induced by intrinsic or environmental factors. To overcome these limitations, this study presents an adaptive Koopman architecture capable of responding to the changes in system dynamics online. The proposed framework initially employs an autoencoder-based neural network that utilizes input-output information from the nominal system to learn the corresponding Koopman embedding offline. Subsequently, we augment this nominal Koopman architecture with a feed-forward neural network that learns to modify the nominal dynamics in response to any deviation between the predicted and observed lifted states, leading to improved generalization and robustness to a wide range of uncertainties and disturbances compared to contemporary methods. Extensive tracking control simulations, which are undertaken by integrating the proposed scheme within a Model Predictive Control framework, are used to highlight its robustness against measurement noise, disturbances, and parametric variations in system dynamics.

A Collision Cone Approach for Control Barrier Functions

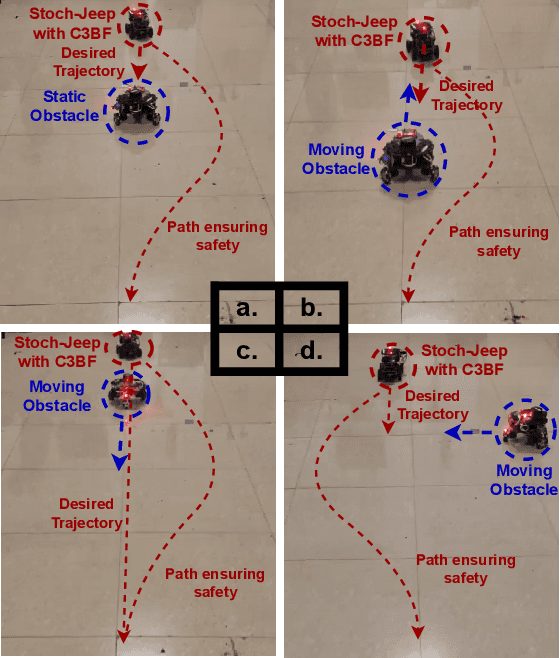
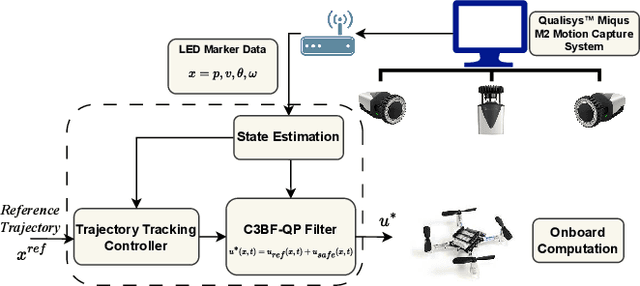
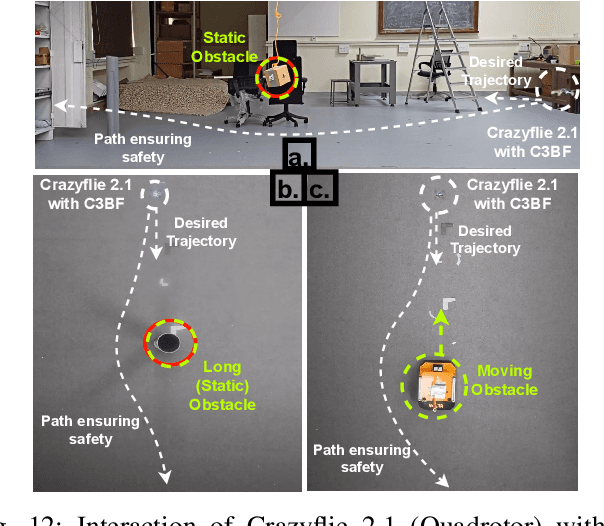
This work presents a unified approach for collision avoidance using Collision-Cone Control Barrier Functions (CBFs) in both ground (UGV) and aerial (UAV) unmanned vehicles. We propose a novel CBF formulation inspired by collision cones, to ensure safety by constraining the relative velocity between the vehicle and the obstacle to always point away from each other. The efficacy of this approach is demonstrated through simulations and hardware implementations on the TurtleBot, Stoch-Jeep, and Crazyflie 2.1 quadrotor robot, showcasing its effectiveness in avoiding collisions with dynamic obstacles in both ground and aerial settings. The real-time controller is developed using CBF Quadratic Programs (CBF-QPs). Comparative analysis with the state-of-the-art CBFs highlights the less conservative nature of the proposed approach. Overall, this research contributes to a novel control formation that can give a guarantee for collision avoidance in unmanned vehicles by modifying the control inputs from existing path-planning controllers.