RN-D: Discretized Categorical Actors with Regularized Networks for On-Policy Reinforcement Learning

On-policy deep reinforcement learning remains a dominant paradigm for continuous control, yet standard implementations rely on Gaussian actors and relatively shallow MLP policies, often leading to brittle optimization when gradients are noisy and policy updates must be conservative. In this paper, we revisit policy representation as a first-class design choice for on-policy optimization. We study discretized categorical actors that represent each action dimension with a distribution over bins, yielding a policy objective that resembles a cross-entropy loss. Building on architectural advances from supervised learning, we further propose regularized actor networks, while keeping critic design fixed. Our results show that simply replacing the standard actor network with our discretized regularized actor yields consistent gains and achieve the state-of-the-art performance across diverse continuous-control benchmarks.

Learning to Nudge: A Scalable Barrier Function Framework for Safe Robot Interaction in Dense Clutter

Robots operating in everyday environments must navigate and manipulate within densely cluttered spaces, where physical contact with surrounding objects is unavoidable. Traditional safety frameworks treat contact as unsafe, restricting robots to collision avoidance and limiting their ability to function in dense, everyday settings. As the number of objects grows, model-based approaches for safe manipulation become computationally intractable; meanwhile, learned methods typically tie safety to the task at hand, making them hard to transfer to new tasks without retraining. In this work we introduce Dense Contact Barrier Functions(DCBF). Our approach bypasses the computational complexity of explicitly modeling multi-object dynamics by instead learning a composable, object-centric function that implicitly captures the safety constraints arising from physical interactions. Trained offline on interactions with a few objects, the learned DCBFcomposes across arbitrary object sets at runtime, producing a single global safety filter that scales linearly and transfers across tasks without retraining. We validate our approach through simulated experiments in dense clutter, demonstrating its ability to enable collision-free navigation and safe, contact-rich interaction in suitable settings.

GLIDE: A Coordinated Aerial-Ground Framework for Search and Rescue in Unknown Environments

We present a cooperative aerial-ground search-and-rescue (SAR) framework that pairs two unmanned aerial vehicles (UAVs) with an unmanned ground vehicle (UGV) to achieve rapid victim localization and obstacle-aware navigation in unknown environments. We dub this framework Guided Long-horizon Integrated Drone Escort (GLIDE), highlighting the UGV's reliance on UAV guidance for long-horizon planning. In our framework, a goal-searching UAV executes real-time onboard victim detection and georeferencing to nominate goals for the ground platform, while a terrain-scouting UAV flies ahead of the UGV's planned route to provide mid-level traversability updates. The UGV fuses aerial cues with local sensing to perform time-efficient A* planning and continuous replanning as information arrives. Additionally, we present a hardware demonstration (using a GEM e6 golf cart as the UGV and two X500 UAVs) to evaluate end-to-end SAR mission performance and include simulation ablations to assess the planning stack in isolation from detection. Empirical results demonstrate that explicit role separation across UAVs, coupled with terrain scouting and guided planning, improves reach time and navigation safety in time-critical SAR missions.

May I have your Attention? Breaking Fine-Tuning based Prompt Injection Defenses using Architecture-Aware Attacks

A popular class of defenses against prompt injection attacks on large language models (LLMs) relies on fine-tuning the model to separate instructions and data, so that the LLM does not follow instructions that might be present with data. There are several academic systems and production-level implementations of this idea. We evaluate the robustness of this class of prompt injection defenses in the whitebox setting by constructing strong optimization-based attacks and showing that the defenses do not provide the claimed security properties. Specifically, we construct a novel attention-based attack algorithm for text-based LLMs and apply it to two recent whitebox defenses SecAlign (CCS 2025) and StruQ (USENIX Security 2025), showing attacks with success rates of up to 70% with modest increase in attacker budget in terms of tokens. Our findings make fundamental progress towards understanding the robustness of prompt injection defenses in the whitebox setting. We release our code and attacks at https://github.com/nishitvp/better_opts_attacks

When Maximum Entropy Misleads Policy Optimization

The Maximum Entropy Reinforcement Learning (MaxEnt RL) framework is a leading approach for achieving efficient learning and robust performance across many RL tasks. However, MaxEnt methods have also been shown to struggle with performance-critical control problems in practice, where non-MaxEnt algorithms can successfully learn. In this work, we analyze how the trade-off between robustness and optimality affects the performance of MaxEnt algorithms in complex control tasks: while entropy maximization enhances exploration and robustness, it can also mislead policy optimization, leading to failure in tasks that require precise, low-entropy policies. Through experiments on a variety of control problems, we concretely demonstrate this misleading effect. Our analysis leads to better understanding of how to balance reward design and entropy maximization in challenging control problems.

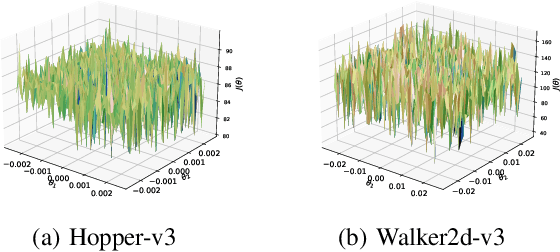
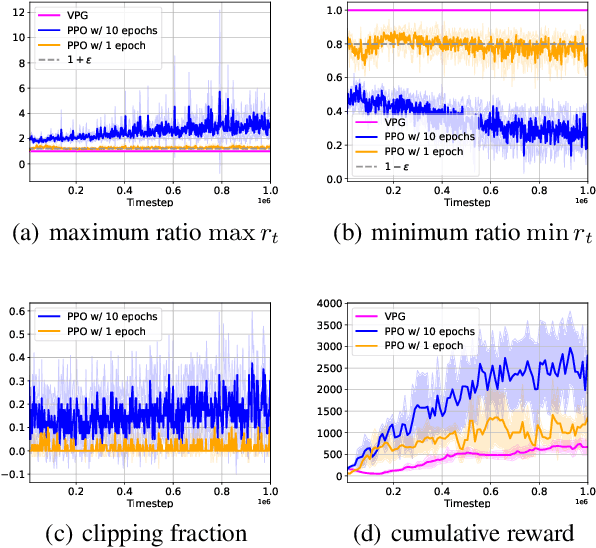
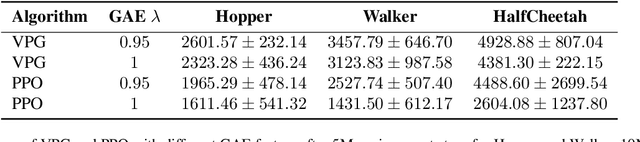
Improving Value Estimation Critically Enhances Vanilla Policy Gradient

Modern policy gradient algorithms, such as TRPO and PPO, outperform vanilla policy gradient in many RL tasks. Questioning the common belief that enforcing approximate trust regions leads to steady policy improvement in practice, we show that the more critical factor is the enhanced value estimation accuracy from more value update steps in each iteration. To demonstrate, we show that by simply increasing the number of value update steps per iteration, vanilla policy gradient itself can achieve performance comparable to or better than PPO in all the standard continuous control benchmark environments. Importantly, this simple change to vanilla policy gradient is significantly more robust to hyperparameter choices, opening up the possibility that RL algorithms may still become more effective and easier to use.

Improving Compositional Generation with Diffusion Models Using Lift Scores

We introduce a novel resampling criterion using lift scores, for improving compositional generation in diffusion models. By leveraging the lift scores, we evaluate whether generated samples align with each single condition and then compose the results to determine whether the composed prompt is satisfied. Our key insight is that lift scores can be efficiently approximated using only the original diffusion model, requiring no additional training or external modules. We develop an optimized variant that achieves relatively lower computational overhead during inference while maintaining effectiveness. Through extensive experiments, we demonstrate that lift scores significantly improved the condition alignment for compositional generation across 2D synthetic data, CLEVR position tasks, and text-to-image synthesis. Our code is available at http://github.com/rainorangelemon/complift.

Safe Human Robot Navigation in Warehouse Scenario

The integration of autonomous mobile robots (AMRs) in industrial environments, particularly warehouses, has revolutionized logistics and operational efficiency. However, ensuring the safety of human workers in dynamic, shared spaces remains a critical challenge. This work proposes a novel methodology that leverages control barrier functions (CBFs) to enhance safety in warehouse navigation. By integrating learning-based CBFs with the Open Robotics Middleware Framework (OpenRMF), the system achieves adaptive and safety-enhanced controls in multi-robot, multi-agent scenarios. Experiments conducted using various robot platforms demonstrate the efficacy of the proposed approach in avoiding static and dynamic obstacles, including human pedestrians. Our experiments evaluate different scenarios in which the number of robots, robot platforms, speed, and number of obstacles are varied, from which we achieve promising performance.

Controllable Motion Generation via Diffusion Modal Coupling

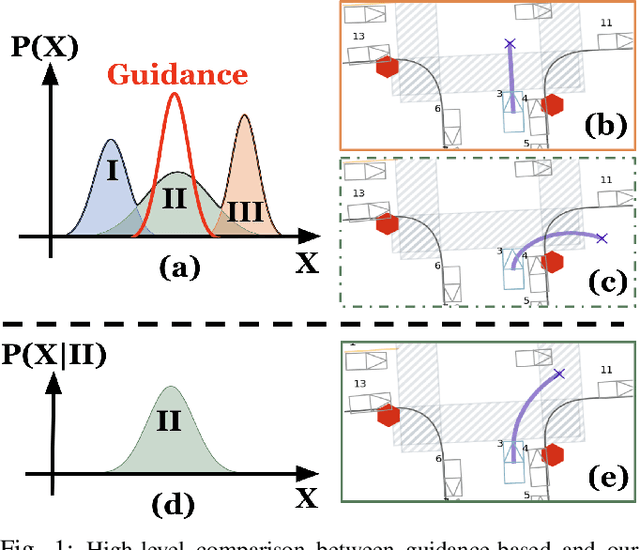
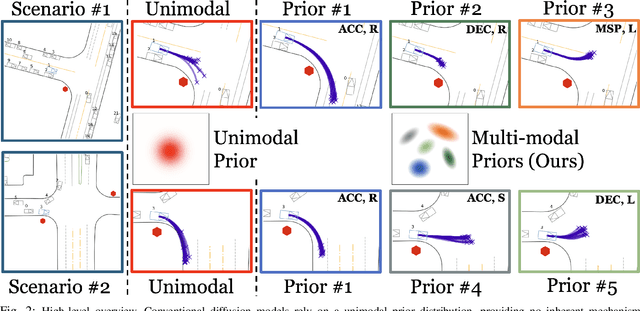
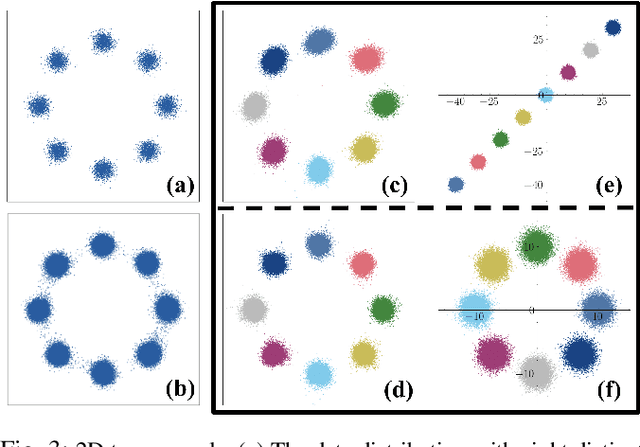
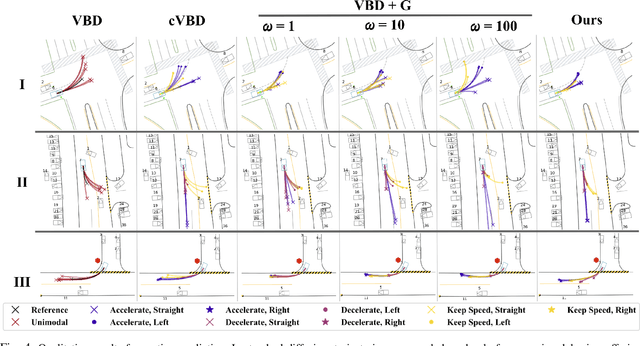
Diffusion models have recently gained significant attention in robotics due to their ability to generate multi-modal distributions of system states and behaviors. However, a key challenge remains: ensuring precise control over the generated outcomes without compromising realism. This is crucial for applications such as motion planning or trajectory forecasting, where adherence to physical constraints and task-specific objectives is essential. We propose a novel framework that enhances controllability in diffusion models by leveraging multi-modal prior distributions and enforcing strong modal coupling. This allows us to initiate the denoising process directly from distinct prior modes that correspond to different possible system behaviors, ensuring sampling to align with the training distribution. We evaluate our approach on motion prediction using the Waymo dataset and multi-task control in Maze2D environments. Experimental results show that our framework outperforms both guidance-based techniques and conditioned models with unimodal priors, achieving superior fidelity, diversity, and controllability, even in the absence of explicit conditioning. Overall, our approach provides a more reliable and scalable solution for controllable motion generation in robotics.

SEEV: Synthesis with Efficient Exact Verification for ReLU Neural Barrier Functions

Neural Control Barrier Functions (NCBFs) have shown significant promise in enforcing safety constraints on nonlinear autonomous systems. State-of-the-art exact approaches to verifying safety of NCBF-based controllers exploit the piecewise-linear structure of ReLU neural networks, however, such approaches still rely on enumerating all of the activation regions of the network near the safety boundary, thus incurring high computation cost. In this paper, we propose a framework for Synthesis with Efficient Exact Verification (SEEV). Our framework consists of two components, namely (i) an NCBF synthesis algorithm that introduces a novel regularizer to reduce the number of activation regions at the safety boundary, and (ii) a verification algorithm that exploits tight over-approximations of the safety conditions to reduce the cost of verifying each piecewise-linear segment. Our simulations show that SEEV significantly improves verification efficiency while maintaining the CBF quality across various benchmark systems and neural network structures. Our code is available at https://github.com/HongchaoZhang-HZ/SEEV.