Hamilton-Jacobi Reachability in Reinforcement Learning: A Survey
Paper and Code
Jul 12, 2024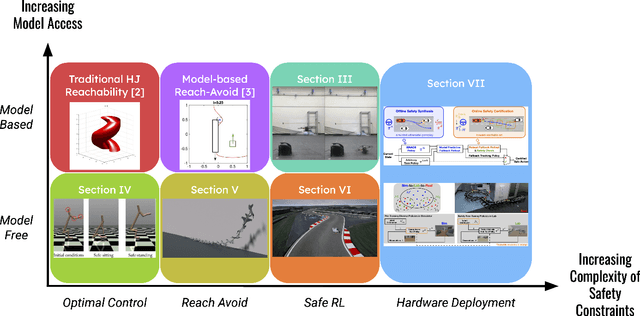


Recent literature has proposed approaches that learn control policies with high performance while maintaining safety guarantees. Synthesizing Hamilton-Jacobi (HJ) reachable sets has become an effective tool for verifying safety and supervising the training of reinforcement learning-based control policies for complex, high-dimensional systems. Previously, HJ reachability was limited to verifying low-dimensional dynamical systems -- this is because the computational complexity of the dynamic programming approach it relied on grows exponentially with the number of system states. To address this limitation, in recent years, there have been methods that compute the reachability value function simultaneously with learning control policies to scale HJ reachability analysis while still maintaining a reliable estimate of the true reachable set. These HJ reachability approximations are used to improve the safety, and even reward performance, of learned control policies and can solve challenging tasks such as those with dynamic obstacles and/or with lidar-based or vision-based observations. In this survey paper, we review the recent developments in the field of HJ reachability estimation in reinforcement learning that would provide a foundational basis for further research into reliability in high-dimensional systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge