Fully Zeroth-Order Bilevel Programming via Gaussian Smoothing

In this paper, we study and analyze zeroth-order stochastic approximation algorithms for solving bilvel problems, when neither the upper/lower objective values, nor their unbiased gradient estimates are available. In particular, exploiting Stein's identity, we first use Gaussian smoothing to estimate first- and second-order partial derivatives of functions with two independent block of variables. We then used these estimates in the framework of a stochastic approximation algorithm for solving bilevel optimization problems and establish its non-asymptotic convergence analysis. To the best of our knowledge, this is the first time that sample complexity bounds are established for a fully stochastic zeroth-order bilevel optimization algorithm.

Stochastic Nested Compositional Bi-level Optimization for Robust Feature Learning

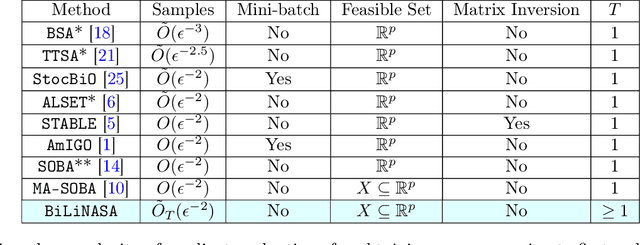
We develop and analyze stochastic approximation algorithms for solving nested compositional bi-level optimization problems. These problems involve a nested composition of $T$ potentially non-convex smooth functions in the upper-level, and a smooth and strongly convex function in the lower-level. Our proposed algorithm does not rely on matrix inversions or mini-batches and can achieve an $\epsilon$-stationary solution with an oracle complexity of approximately $\tilde{O}_T(1/\epsilon^{2})$, assuming the availability of stochastic first-order oracles for the individual functions in the composition and the lower-level, which are unbiased and have bounded moments. Here, $\tilde{O}_T$ hides polylog factors and constants that depend on $T$. The key challenge we address in establishing this result relates to handling three distinct sources of bias in the stochastic gradients. The first source arises from the compositional nature of the upper-level, the second stems from the bi-level structure, and the third emerges due to the utilization of Neumann series approximations to avoid matrix inversion. To demonstrate the effectiveness of our approach, we apply it to the problem of robust feature learning for deep neural networks under covariate shift, showcasing the benefits and advantages of our methodology in that context.

Learn What NOT to Learn: Towards Generative Safety in Chatbots

Conversational models that are generative and open-domain are particularly susceptible to generating unsafe content since they are trained on web-based social data. Prior approaches to mitigating this issue have drawbacks, such as disrupting the flow of conversation, limited generalization to unseen toxic input contexts, and sacrificing the quality of the dialogue for the sake of safety. In this paper, we present a novel framework, named "LOT" (Learn NOT to), that employs a contrastive loss to enhance generalization by learning from both positive and negative training signals. Our approach differs from the standard contrastive learning framework in that it automatically obtains positive and negative signals from the safe and unsafe language distributions that have been learned beforehand. The LOT framework utilizes divergence to steer the generations away from the unsafe subspace and towards the safe subspace while sustaining the flow of conversation. Our approach is memory and time-efficient during decoding and effectively reduces toxicity while preserving engagingness and fluency. Empirical results indicate that LOT reduces toxicity by up to four-fold while achieving four to six-fold higher rates of engagingness and fluency compared to baseline models. Our findings are further corroborated by human evaluation.

A One-Sample Decentralized Proximal Algorithm for Non-Convex Stochastic Composite Optimization

We focus on decentralized stochastic non-convex optimization, where $n$ agents work together to optimize a composite objective function which is a sum of a smooth term and a non-smooth convex term. To solve this problem, we propose two single-time scale algorithms: Prox-DASA and Prox-DASA-GT. These algorithms can find $\epsilon$-stationary points in $\mathcal{O}(n^{-1}\epsilon^{-2})$ iterations using constant batch sizes (i.e., $\mathcal{O}(1)$). Unlike prior work, our algorithms achieve a comparable complexity result without requiring large batch sizes, more complex per-iteration operations (such as double loops), or stronger assumptions. Our theoretical findings are supported by extensive numerical experiments, which demonstrate the superiority of our algorithms over previous approaches.

Projection-free Constrained Stochastic Nonconvex Optimization with State-dependent Markov Data

We study a projection-free conditional gradient-type algorithm for constrained nonconvex stochastic optimization problems with Markovian data. In particular, we focus on the case when the transition kernel of the Markov chain is state-dependent. Such stochastic optimization problems arise in various machine learning problems including strategic classification and reinforcement learning. For this problem, we establish that the number of calls to the stochastic first-order oracle and the linear minimization oracle to obtain an appropriately defined $\epsilon$-stationary point, are of the order $\mathcal{O}(1/\epsilon^{2.5})$ and $\mathcal{O}(1/\epsilon^{5.5})$ respectively. We also empirically demonstrate the performance of our algorithm on the problem of strategic classification with neural networks.

RIGID: Robust Linear Regression with Missing Data

We present a robust framework to perform linear regression with missing entries in the features. By considering an elliptical data distribution, and specifically a multivariate normal model, we are able to conditionally formulate a distribution for the missing entries and present a robust framework, which minimizes the worst case error caused by the uncertainty about the missing data. We show that the proposed formulation, which naturally takes into account the dependency between different variables, ultimately reduces to a convex program, for which a customized and scalable solver can be delivered. In addition to a detailed analysis to deliver such solver, we also asymptoticly analyze the behavior of the proposed framework, and present technical discussions to estimate the required input parameters. We complement our analysis with experiments performed on synthetic, semi-synthetic, and real data, and show how the proposed formulation improves the prediction accuracy and robustness, and outperforms the competing techniques.

A Projection-free Algorithm for Constrained Stochastic Multi-level Composition Optimization

We propose a projection-free conditional gradient-type algorithm for smooth stochastic multi-level composition optimization, where the objective function is a nested composition of $T$ functions and the constraint set is a closed convex set. Our algorithm assumes access to noisy evaluations of the functions and their gradients, through a stochastic first-order oracle satisfying certain standard unbiasedness and second moment assumptions. We show that the number of calls to the stochastic first-order oracle and the linear-minimization oracle required by the proposed algorithm, to obtain an $\epsilon$-stationary solution, are of order $\mathcal{O}_T(\epsilon^{-2})$ and $\mathcal{O}_T(\epsilon^{-3})$ respectively, where $\mathcal{O}_T$ hides constants in $T$. Notably, the dependence of these complexity bounds on $\epsilon$ and $T$ are separate in the sense that changing one does not impact the dependence of the bounds on the other. Moreover, our algorithm is parameter-free and does not require any (increasing) order of mini-batches to converge unlike the common practice in the analysis of stochastic conditional gradient-type algorithms.

The Parametric Cost Function Approximation: A new approach for multistage stochastic programming

The most common approaches for solving multistage stochastic programming problems in the research literature have been to either use value functions ("dynamic programming") or scenario trees ("stochastic programming") to approximate the impact of a decision now on the future. By contrast, common industry practice is to use a deterministic approximation of the future which is easier to understand and solve, but which is criticized for ignoring uncertainty. We show that a parameterized version of a deterministic optimization model can be an effective way of handling uncertainty without the complexity of either stochastic programming or dynamic programming. We present the idea of a parameterized deterministic optimization model, and in particular a deterministic lookahead model, as a powerful strategy for many complex stochastic decision problems. This approach can handle complex, high-dimensional state variables, and avoids the usual approximations associated with scenario trees or value function approximations. Instead, it introduces the offline challenge of designing and tuning the parameterization. We illustrate the idea by using a series of application settings, and demonstrate its use in a nonstationary energy storage problem with rolling forecasts.

Escaping Saddle-Points Faster under Interpolation-like Conditions

In this paper, we show that under over-parametrization several standard stochastic optimization algorithms escape saddle-points and converge to local-minimizers much faster. One of the fundamental aspects of over-parametrized models is that they are capable of interpolating the training data. We show that, under interpolation-like assumptions satisfied by the stochastic gradients in an over-parametrization setting, the first-order oracle complexity of Perturbed Stochastic Gradient Descent (PSGD) algorithm to reach an $\epsilon$-local-minimizer, matches the corresponding deterministic rate of $\tilde{\mathcal{O}}(1/\epsilon^{2})$. We next analyze Stochastic Cubic-Regularized Newton (SCRN) algorithm under interpolation-like conditions, and show that the oracle complexity to reach an $\epsilon$-local-minimizer under interpolation-like conditions, is $\tilde{\mathcal{O}}(1/\epsilon^{2.5})$. While this obtained complexity is better than the corresponding complexity of either PSGD, or SCRN without interpolation-like assumptions, it does not match the rate of $\tilde{\mathcal{O}}(1/\epsilon^{1.5})$ corresponding to deterministic Cubic-Regularized Newton method. It seems further Hessian-based interpolation-like assumptions are necessary to bridge this gap. We also discuss the corresponding improved complexities in the zeroth-order settings.

Stochastic Multi-level Composition Optimization Algorithms with Level-Independent Convergence Rates

In this paper, we study smooth stochastic multi-level composition optimization problems, where the objective function is a nested composition of $T$ functions. We assume access to noisy evaluations of the functions and their gradients, through a stochastic first-order oracle. For solving this class of problems, we propose two algorithms using moving-average stochastic estimates, and analyze their convergence to an $\epsilon$-stationary point of the problem. We show that the first algorithm, which is a generalization of [22] to the $T$ level case, can achieve a sample complexity of $\mathcal{O}(1/\epsilon^6)$ by using mini-batches of samples in each iteration. By modifying this algorithm using linearized stochastic estimates of the function values, we improve the sample complexity to $\mathcal{O}(1/\epsilon^4)$. This modification also removes the requirement of having a mini-batch of samples in each iteration. To the best of our knowledge, this is the first time that such an online algorithm designed for the (un)constrained multi-level setting, obtains the same sample complexity of the smooth single-level setting, under mild assumptions on the stochastic first-order oracle.