Fully First-Order Methods for Decentralized Bilevel Optimization

This paper focuses on decentralized stochastic bilevel optimization (DSBO) where agents only communicate with their neighbors. We propose Decentralized Stochastic Gradient Descent and Ascent with Gradient Tracking (DSGDA-GT), a novel algorithm that only requires first-order oracles that are much cheaper than second-order oracles widely adopted in existing works. We further provide a finite-time convergence analysis showing that for $n$ agents collaboratively solving the DSBO problem, the sample complexity of finding an $\epsilon$-stationary point in our algorithm is $\mathcal{O}(n^{-1}\epsilon^{-7})$, which matches the currently best-known results of the single-agent counterpart with linear speedup. The numerical experiments demonstrate both the communication and training efficiency of our algorithm.

Stochastic Optimization Algorithms for Instrumental Variable Regression with Streaming Data

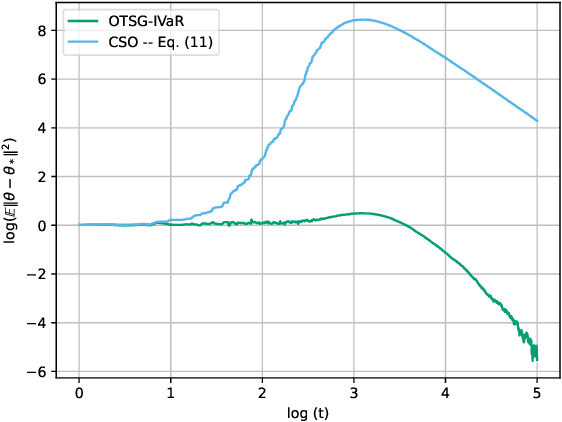
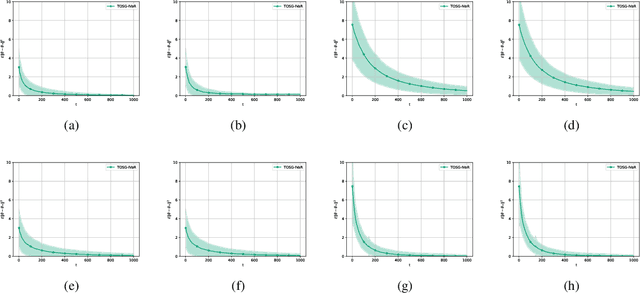
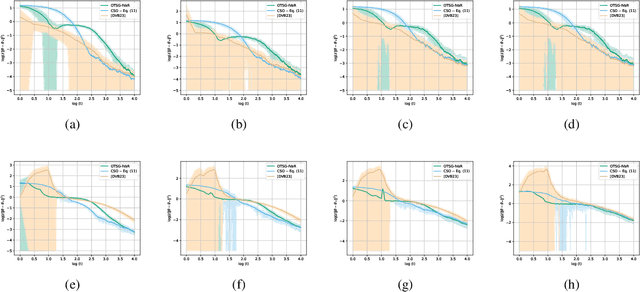
We develop and analyze algorithms for instrumental variable regression by viewing the problem as a conditional stochastic optimization problem. In the context of least-squares instrumental variable regression, our algorithms neither require matrix inversions nor mini-batches and provides a fully online approach for performing instrumental variable regression with streaming data. When the true model is linear, we derive rates of convergence in expectation, that are of order $\mathcal{O}(\log T/T)$ and $\mathcal{O}(1/T^{1-\iota})$ for any $\iota>0$, respectively under the availability of two-sample and one-sample oracles, respectively, where $T$ is the number of iterations. Importantly, under the availability of the two-sample oracle, our procedure avoids explicitly modeling and estimating the relationship between confounder and the instrumental variables, demonstrating the benefit of the proposed approach over recent works based on reformulating the problem as minimax optimization problems. Numerical experiments are provided to corroborate the theoretical results.

From Stability to Chaos: Analyzing Gradient Descent Dynamics in Quadratic Regression

We conduct a comprehensive investigation into the dynamics of gradient descent using large-order constant step-sizes in the context of quadratic regression models. Within this framework, we reveal that the dynamics can be encapsulated by a specific cubic map, naturally parameterized by the step-size. Through a fine-grained bifurcation analysis concerning the step-size parameter, we delineate five distinct training phases: (1) monotonic, (2) catapult, (3) periodic, (4) chaotic, and (5) divergent, precisely demarcating the boundaries of each phase. As illustrations, we provide examples involving phase retrieval and two-layer neural networks employing quadratic activation functions and constant outer-layers, utilizing orthogonal training data. Our simulations indicate that these five phases also manifest with generic non-orthogonal data. We also empirically investigate the generalization performance when training in the various non-monotonic (and non-divergent) phases. In particular, we observe that performing an ergodic trajectory averaging stabilizes the test error in non-monotonic (and non-divergent) phases.

Stochastic Nested Compositional Bi-level Optimization for Robust Feature Learning

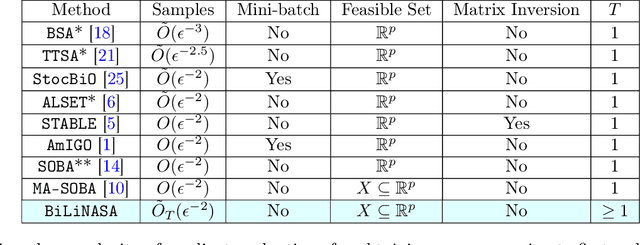
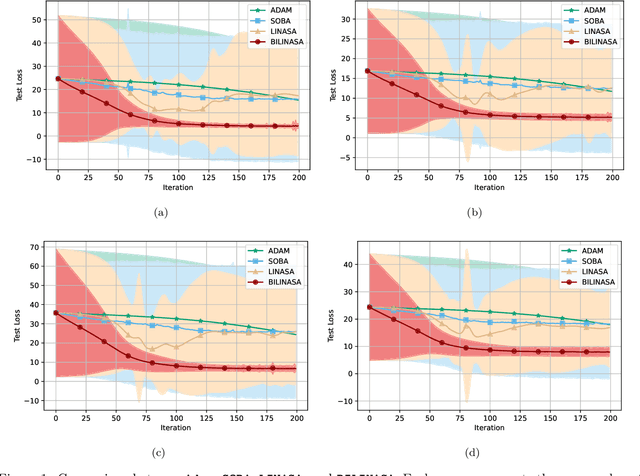
We develop and analyze stochastic approximation algorithms for solving nested compositional bi-level optimization problems. These problems involve a nested composition of $T$ potentially non-convex smooth functions in the upper-level, and a smooth and strongly convex function in the lower-level. Our proposed algorithm does not rely on matrix inversions or mini-batches and can achieve an $\epsilon$-stationary solution with an oracle complexity of approximately $\tilde{O}_T(1/\epsilon^{2})$, assuming the availability of stochastic first-order oracles for the individual functions in the composition and the lower-level, which are unbiased and have bounded moments. Here, $\tilde{O}_T$ hides polylog factors and constants that depend on $T$. The key challenge we address in establishing this result relates to handling three distinct sources of bias in the stochastic gradients. The first source arises from the compositional nature of the upper-level, the second stems from the bi-level structure, and the third emerges due to the utilization of Neumann series approximations to avoid matrix inversion. To demonstrate the effectiveness of our approach, we apply it to the problem of robust feature learning for deep neural networks under covariate shift, showcasing the benefits and advantages of our methodology in that context.

Optimal Algorithms for Stochastic Bilevel Optimization under Relaxed Smoothness Conditions

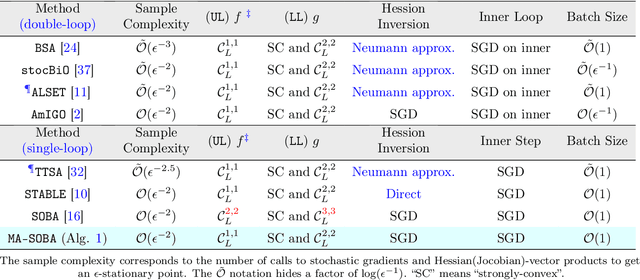
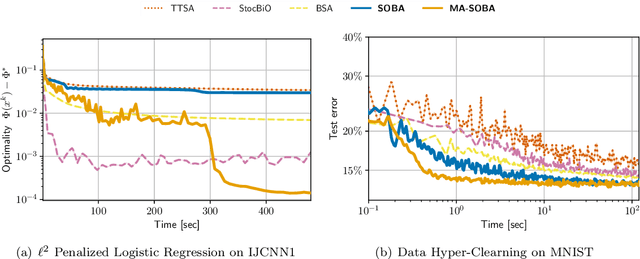
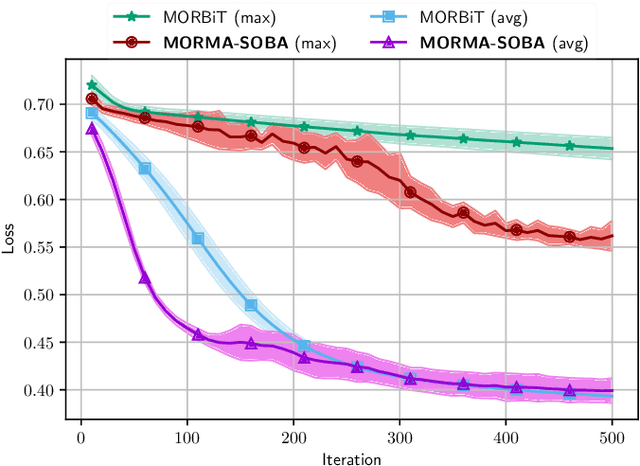
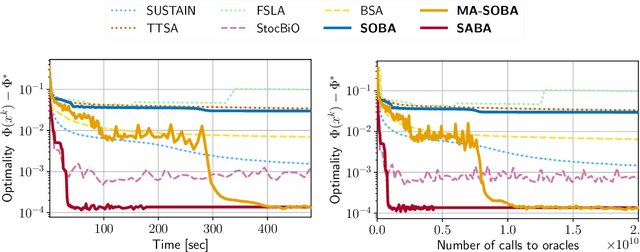
Stochastic Bilevel optimization usually involves minimizing an upper-level (UL) function that is dependent on the arg-min of a strongly-convex lower-level (LL) function. Several algorithms utilize Neumann series to approximate certain matrix inverses involved in estimating the implicit gradient of the UL function (hypergradient). The state-of-the-art StOchastic Bilevel Algorithm (SOBA) [16] instead uses stochastic gradient descent steps to solve the linear system associated with the explicit matrix inversion. This modification enables SOBA to match the lower bound of sample complexity for the single-level counterpart in non-convex settings. Unfortunately, the current analysis of SOBA relies on the assumption of higher-order smoothness for the UL and LL functions to achieve optimality. In this paper, we introduce a novel fully single-loop and Hessian-inversion-free algorithmic framework for stochastic bilevel optimization and present a tighter analysis under standard smoothness assumptions (first-order Lipschitzness of the UL function and second-order Lipschitzness of the LL function). Furthermore, we show that by a slight modification of our approach, our algorithm can handle a more general multi-objective robust bilevel optimization problem. For this case, we obtain the state-of-the-art oracle complexity results demonstrating the generality of both the proposed algorithmic and analytic frameworks. Numerical experiments demonstrate the performance gain of the proposed algorithms over existing ones.

A One-Sample Decentralized Proximal Algorithm for Non-Convex Stochastic Composite Optimization

We focus on decentralized stochastic non-convex optimization, where $n$ agents work together to optimize a composite objective function which is a sum of a smooth term and a non-smooth convex term. To solve this problem, we propose two single-time scale algorithms: Prox-DASA and Prox-DASA-GT. These algorithms can find $\epsilon$-stationary points in $\mathcal{O}(n^{-1}\epsilon^{-2})$ iterations using constant batch sizes (i.e., $\mathcal{O}(1)$). Unlike prior work, our algorithms achieve a comparable complexity result without requiring large batch sizes, more complex per-iteration operations (such as double loops), or stronger assumptions. Our theoretical findings are supported by extensive numerical experiments, which demonstrate the superiority of our algorithms over previous approaches.

Decentralized Stochastic Bilevel Optimization with Improved Per-Iteration Complexity

Bilevel optimization recently has received tremendous attention due to its great success in solving important machine learning problems like meta learning, reinforcement learning, and hyperparameter optimization. Extending single-agent training on bilevel problems to the decentralized setting is a natural generalization, and there has been a flurry of work studying decentralized bilevel optimization algorithms. However, it remains unknown how to design the distributed algorithm with sample complexity and convergence rate comparable to SGD for stochastic optimization, and at the same time without directly computing the exact Hessian or Jacobian matrices. In this paper we propose such an algorithm. More specifically, we propose a novel decentralized stochastic bilevel optimization (DSBO) algorithm that only requires first order stochastic oracle, Hessian-vector product and Jacobian-vector product oracle. The sample complexity of our algorithm matches the currently best known results for DSBO, and the advantage of our algorithm is that it does not require estimating the full Hessian and Jacobian matrices, thereby having improved per-iteration complexity.