From Stability to Chaos: Analyzing Gradient Descent Dynamics in Quadratic Regression

We conduct a comprehensive investigation into the dynamics of gradient descent using large-order constant step-sizes in the context of quadratic regression models. Within this framework, we reveal that the dynamics can be encapsulated by a specific cubic map, naturally parameterized by the step-size. Through a fine-grained bifurcation analysis concerning the step-size parameter, we delineate five distinct training phases: (1) monotonic, (2) catapult, (3) periodic, (4) chaotic, and (5) divergent, precisely demarcating the boundaries of each phase. As illustrations, we provide examples involving phase retrieval and two-layer neural networks employing quadratic activation functions and constant outer-layers, utilizing orthogonal training data. Our simulations indicate that these five phases also manifest with generic non-orthogonal data. We also empirically investigate the generalization performance when training in the various non-monotonic (and non-divergent) phases. In particular, we observe that performing an ergodic trajectory averaging stabilizes the test error in non-monotonic (and non-divergent) phases.

DISeR: Designing Imaging Systems with Reinforcement Learning

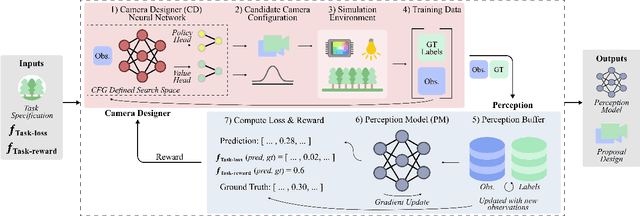
Imaging systems consist of cameras to encode visual information about the world and perception models to interpret this encoding. Cameras contain (1) illumination sources, (2) optical elements, and (3) sensors, while perception models use (4) algorithms. Directly searching over all combinations of these four building blocks to design an imaging system is challenging due to the size of the search space. Moreover, cameras and perception models are often designed independently, leading to sub-optimal task performance. In this paper, we formulate these four building blocks of imaging systems as a context-free grammar (CFG), which can be automatically searched over with a learned camera designer to jointly optimize the imaging system with task-specific perception models. By transforming the CFG to a state-action space, we then show how the camera designer can be implemented with reinforcement learning to intelligently search over the combinatorial space of possible imaging system configurations. We demonstrate our approach on two tasks, depth estimation and camera rig design for autonomous vehicles, showing that our method yields rigs that outperform industry-wide standards. We believe that our proposed approach is an important step towards automating imaging system design.

High-dimensional Central Limit Theorems for Linear Functionals of Online Least-Squares SGD

Stochastic gradient descent (SGD) has emerged as the quintessential method in a data scientist's toolbox. Much progress has been made in the last two decades toward understanding the iteration complexity of SGD (in expectation and high-probability) in the learning theory and optimization literature. However, using SGD for high-stakes applications requires careful quantification of the associated uncertainty. Toward that end, in this work, we establish high-dimensional Central Limit Theorems (CLTs) for linear functionals of online least-squares SGD iterates under a Gaussian design assumption. Our main result shows that a CLT holds even when the dimensionality is of order exponential in the number of iterations of the online SGD, thereby enabling high-dimensional inference with online SGD. Our proof technique involves leveraging Berry-Esseen bounds developed for martingale difference sequences and carefully evaluating the required moment and quadratic variation terms through recent advances in concentration inequalities for product random matrices. We also provide an online approach for estimating the variance appearing in the CLT (required for constructing confidence intervals in practice) and establish consistency results in the high-dimensional setting.