Bilevel Optimization for Planning through Contact: A Semidirect Method

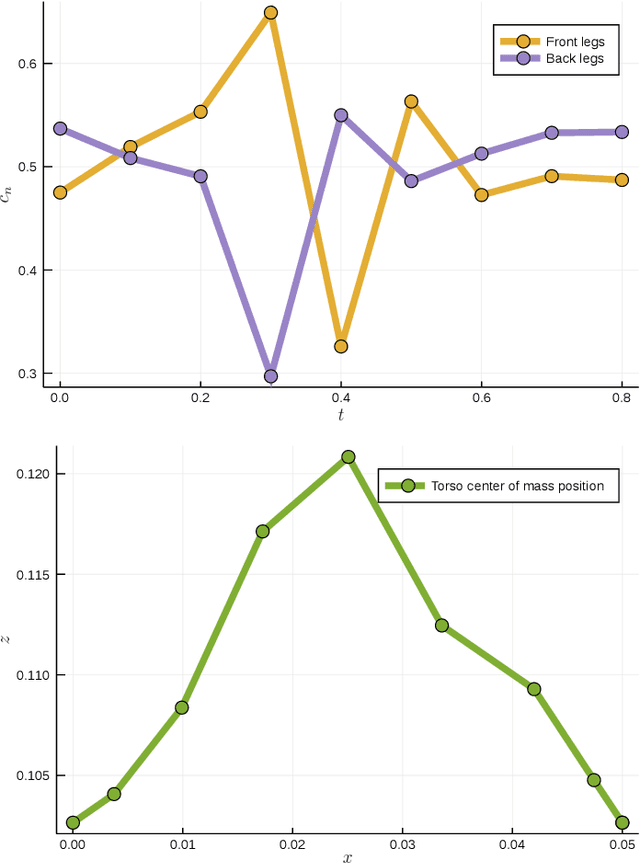
Many robotics applications, from object manipulation to locomotion, require planning methods that are capable of handling the dynamics of contact. Trajectory optimization has been shown to be a viable approach that can be made to support contact dynamics. However, the current state-of-the art methods remain slow and are often difficult to get to converge. In this work, we leverage recent advances in bilevel optimization to design an algorithm capable of efficiently generating trajectories that involve making and breaking contact. We demonstrate our method's efficiency by outperforming an alternative state-of-the-art method on a benchmark problem. We moreover demonstrate the method's ability to design a simple periodic gait for a quadruped with 15 degrees of freedom and four contact points.