Soft Robot Optimal Control Via Reduced Order Finite Element Models

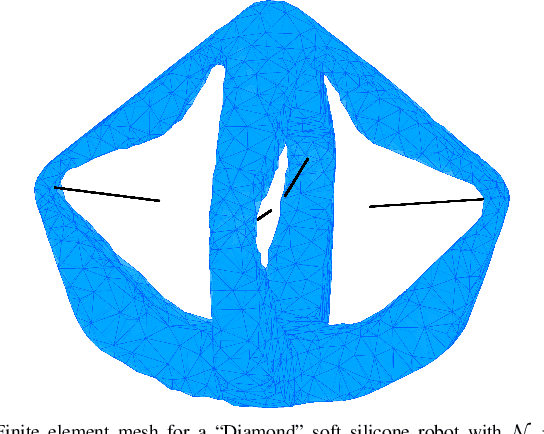
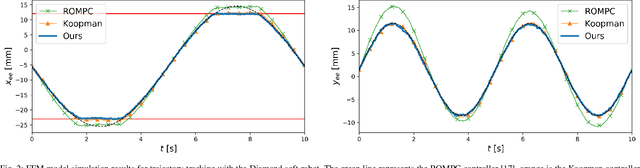
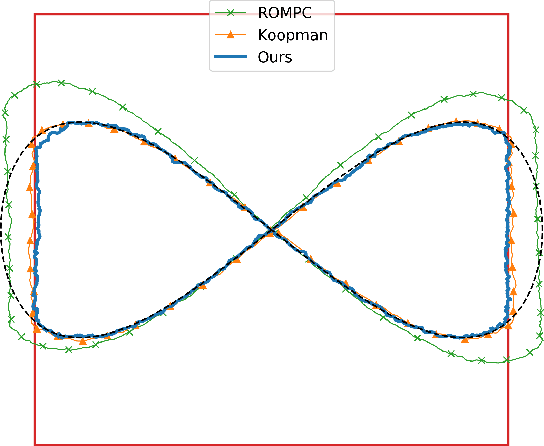
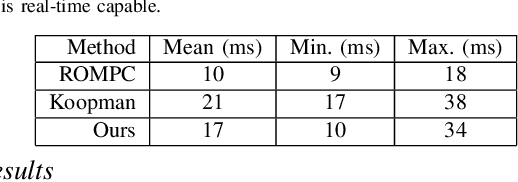
Finite element methods have been successfully used to develop physics-based models of soft robots that capture the nonlinear dynamic behavior induced by continuous deformation. These high-fidelity models are therefore ideal for designing controllers for complex dynamic tasks such as trajectory optimization and trajectory tracking. However, finite element models are also typically very high-dimensional, which makes real-time control challenging. In this work we propose an approach for finite element model-based control of soft robots that leverages model order reduction techniques to significantly increase computational efficiency. In particular, a constrained optimal control problem is formulated based on a nonlinear reduced order finite element model and is solved via sequential convex programming. This approach is demonstrated through simulation of a cable-driven soft robot for a constrained trajectory tracking task, where a 9768-dimensional finite element model is used for controller design.

Bilevel Optimization for Planning through Contact: A Semidirect Method

Many robotics applications, from object manipulation to locomotion, require planning methods that are capable of handling the dynamics of contact. Trajectory optimization has been shown to be a viable approach that can be made to support contact dynamics. However, the current state-of-the art methods remain slow and are often difficult to get to converge. In this work, we leverage recent advances in bilevel optimization to design an algorithm capable of efficiently generating trajectories that involve making and breaking contact. We demonstrate our method's efficiency by outperforming an alternative state-of-the-art method on a benchmark problem. We moreover demonstrate the method's ability to design a simple periodic gait for a quadruped with 15 degrees of freedom and four contact points.