Back to Base: Towards Hands-Off Learning via Safe Resets with Reach-Avoid Safety Filters

Designing controllers that accomplish tasks while guaranteeing safety constraints remains a significant challenge. We often want an agent to perform well in a nominal task, such as environment exploration, while ensuring it can avoid unsafe states and return to a desired target by a specific time. In particular we are motivated by the setting of safe, efficient, hands-off training for reinforcement learning in the real world. By enabling a robot to safely and autonomously reset to a desired region (e.g., charging stations) without human intervention, we can enhance efficiency and facilitate training. Safety filters, such as those based on control barrier functions, decouple safety from nominal control objectives and rigorously guarantee safety. Despite their success, constructing these functions for general nonlinear systems with control constraints and system uncertainties remains an open problem. This paper introduces a safety filter obtained from the value function associated with the reach-avoid problem. The proposed safety filter minimally modifies the nominal controller while avoiding unsafe regions and guiding the system back to the desired target set. By preserving policy performance while allowing safe resetting, we enable efficient hands-off reinforcement learning and advance the feasibility of safe training for real world robots. We demonstrate our approach using a modified version of soft actor-critic to safely train a swing-up task on a modified cartpole stabilization problem.

Categorical Traffic Transformer: Interpretable and Diverse Behavior Prediction with Tokenized Latent

Adept traffic models are critical to both planning and closed-loop simulation for autonomous vehicles (AV), and key design objectives include accuracy, diverse multimodal behaviors, interpretability, and downstream compatibility. Recently, with the advent of large language models (LLMs), an additional desirable feature for traffic models is LLM compatibility. We present Categorical Traffic Transformer (CTT), a traffic model that outputs both continuous trajectory predictions and tokenized categorical predictions (lane modes, homotopies, etc.). The most outstanding feature of CTT is its fully interpretable latent space, which enables direct supervision of the latent variable from the ground truth during training and avoids mode collapse completely. As a result, CTT can generate diverse behaviors conditioned on different latent modes with semantic meanings while beating SOTA on prediction accuracy. In addition, CTT's ability to input and output tokens enables integration with LLMs for common-sense reasoning and zero-shot generalization.

Patching Neural Barrier Functions Using Hamilton-Jacobi Reachability

Learning-based control algorithms have led to major advances in robotics at the cost of decreased safety guarantees. Recently, neural networks have also been used to characterize safety through the use of barrier functions for complex nonlinear systems. Learned barrier functions approximately encode and enforce a desired safety constraint through a value function, but do not provide any formal guarantees. In this paper, we propose a local dynamic programming (DP) based approach to "patch" an almost-safe learned barrier at potentially unsafe points in the state space. This algorithm, HJ-Patch, obtains a novel barrier that provides formal safety guarantees, yet retains the global structure of the learned barrier. Our local DP based reachability algorithm, HJ-Patch, updates the barrier function "minimally" at points that both (a) neighbor the barrier safety boundary and (b) do not satisfy the safety condition. We view this as a key step to bridging the gap between learning-based barrier functions and Hamilton-Jacobi reachability analysis, providing a framework for further integration of these approaches. We demonstrate that for well-trained barriers we reduce the computational load by 2 orders of magnitude with respect to standard DP-based reachability, and demonstrate scalability to a 6-dimensional system, which is at the limit of standard DP-based reachability.

Refining Control Barrier Functions through Hamilton-Jacobi Reachability

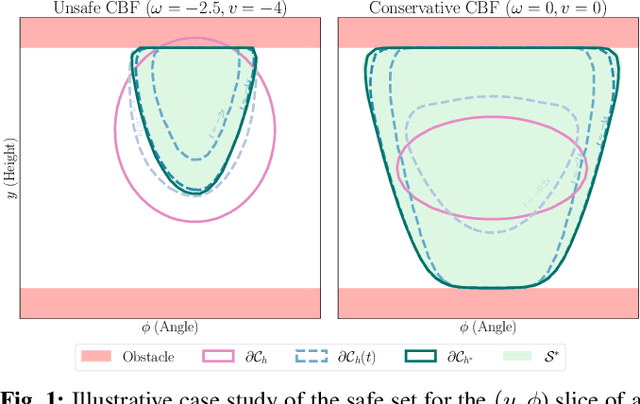
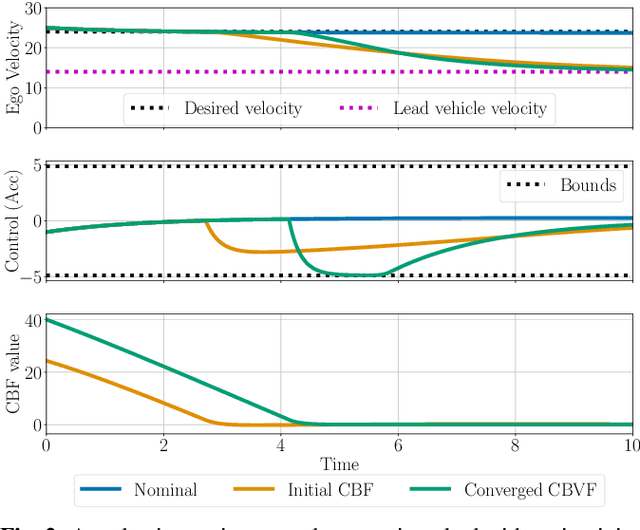
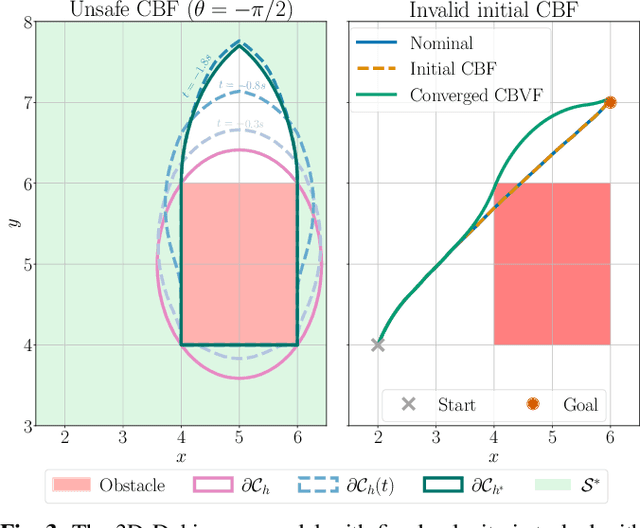
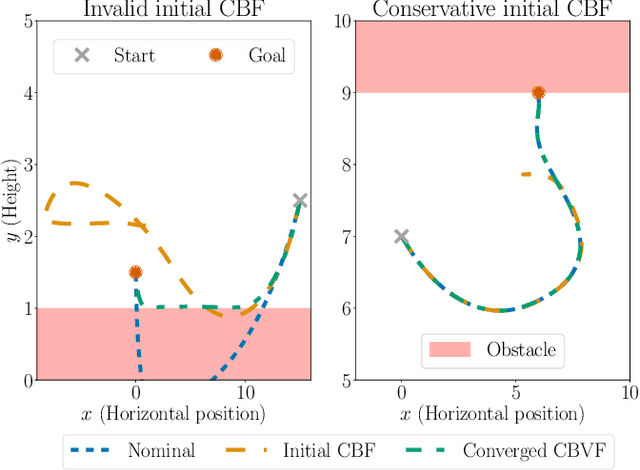
Safety filters based on Control Barrier Functions (CBFs) have emerged as a practical tool for the safety-critical control of autonomous systems. These approaches encode safety through a value function and enforce safety by imposing a constraint on the time derivative of this value function. However, synthesizing a valid CBF that is not overly conservative in the presence of input constraints is a notorious challenge. In this work, we propose refining candidate CBFs using formal verification methods to obtain a valid CBF. In particular, we update an expert-synthesized or backup CBF using dynamic programming (DP) based reachability analysis. Our framework guarantees that with every DP iteration the obtained CBF is provably at least as safe as the prior iteration and converges to a valid CBF. Therefore, our proposed method can be used in-the-loop for robotic systems. We demonstrate the practicality of our method to enhance safety and/or reduce conservativeness on a range of nonlinear control-affine systems using various CBF synthesis techniques in simulation.

Soft Robot Optimal Control Via Reduced Order Finite Element Models

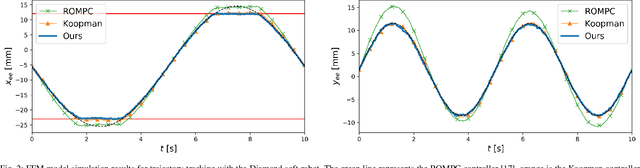
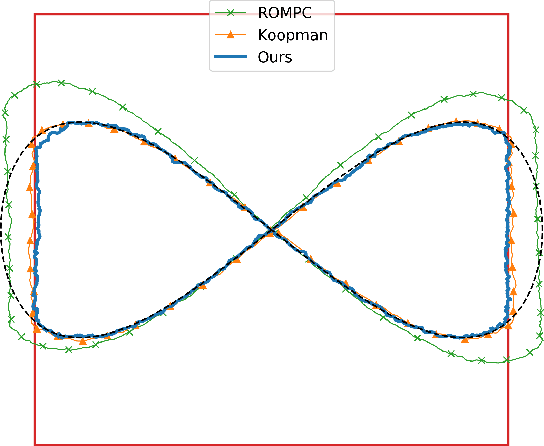
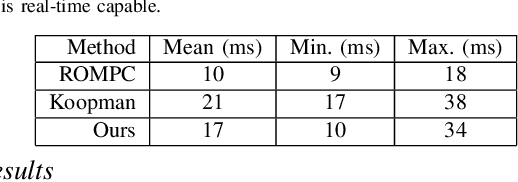
Finite element methods have been successfully used to develop physics-based models of soft robots that capture the nonlinear dynamic behavior induced by continuous deformation. These high-fidelity models are therefore ideal for designing controllers for complex dynamic tasks such as trajectory optimization and trajectory tracking. However, finite element models are also typically very high-dimensional, which makes real-time control challenging. In this work we propose an approach for finite element model-based control of soft robots that leverages model order reduction techniques to significantly increase computational efficiency. In particular, a constrained optimal control problem is formulated based on a nonlinear reduced order finite element model and is solved via sequential convex programming. This approach is demonstrated through simulation of a cable-driven soft robot for a constrained trajectory tracking task, where a 9768-dimensional finite element model is used for controller design.