Gaussian Process Constraint Learning for Scalable Chance-Constrained Motion Planning from Demonstrations
Paper and Code
Dec 08, 2021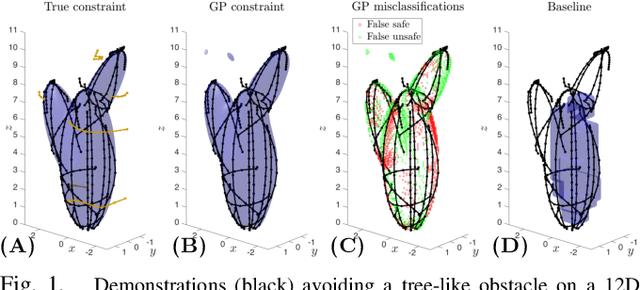
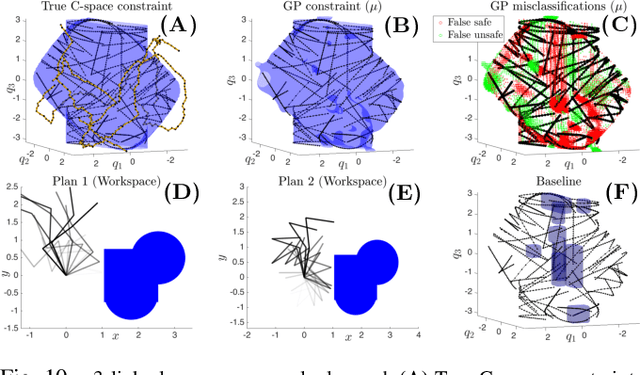
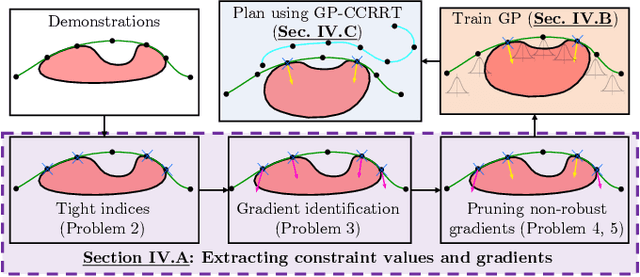
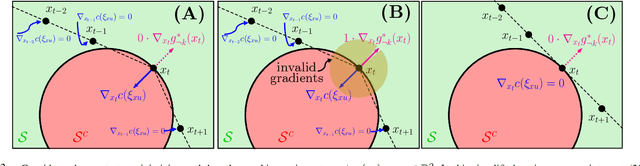
We propose a method for learning constraints represented as Gaussian processes (GPs) from locally-optimal demonstrations. Our approach uses the Karush-Kuhn-Tucker (KKT) optimality conditions to determine where on the demonstrations the constraint is tight, and a scaling of the constraint gradient at those states. We then train a GP representation of the constraint which is consistent with and which generalizes this information. We further show that the GP uncertainty can be used within a kinodynamic RRT to plan probabilistically-safe trajectories, and that we can exploit the GP structure within the planner to exactly achieve a specified safety probability. We demonstrate our method can learn complex, nonlinear constraints demonstrated on a 5D nonholonomic car, a 12D quadrotor, and a 3-link planar arm, all while requiring minimal prior information on the constraint. Our results suggest the learned GP constraint is accurate, outperforming previous constraint learning methods that require more a priori knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge