Semantic Routing: Exploring Multi-Layer LLM Feature Weighting for Diffusion Transformers

Recent DiT-based text-to-image models increasingly adopt LLMs as text encoders, yet text conditioning remains largely static and often utilizes only a single LLM layer, despite pronounced semantic hierarchy across LLM layers and non-stationary denoising dynamics over both diffusion time and network depth. To better match the dynamic process of DiT generation and thereby enhance the diffusion model's generative capability, we introduce a unified normalized convex fusion framework equipped with lightweight gates to systematically organize multi-layer LLM hidden states via time-wise, depth-wise, and joint fusion. Experiments establish Depth-wise Semantic Routing as the superior conditioning strategy, consistently improving text-image alignment and compositional generation (e.g., +9.97 on the GenAI-Bench Counting task). Conversely, we find that purely time-wise fusion can paradoxically degrade visual generation fidelity. We attribute this to a train-inference trajectory mismatch: under classifier-free guidance, nominal timesteps fail to track the effective SNR, causing semantically mistimed feature injection during inference. Overall, our results position depth-wise routing as a strong and effective baseline and highlight the critical need for trajectory-aware signals to enable robust time-dependent conditioning.

Learning the Mechanism of Catastrophic Forgetting: A Perspective from Gradient Similarity

Catastrophic forgetting during knowledge injection severely undermines the continual learning capability of large language models (LLMs). Although existing methods attempt to mitigate this issue, they often lack a foundational theoretical explanation. We establish a gradient-based theoretical framework to explain catastrophic forgetting. We first prove that strongly negative gradient similarity is a fundamental cause of forgetting. We then use gradient similarity to identify two types of neurons: conflicting neurons that induce forgetting and account for 50%-75% of neurons, and collaborative neurons that mitigate forgetting and account for 25%-50%. Based on this analysis, we propose a knowledge injection method, Collaborative Neural Learning (CNL). By freezing conflicting neurons and updating only collaborative neurons, CNL theoretically eliminates catastrophic forgetting under an infinitesimal learning rate eta and an exactly known mastered set. Experiments on five LLMs, four datasets, and four optimizers show that CNL achieves zero forgetting in in-set settings and reduces forgetting by 59.1%-81.7% in out-of-set settings.

Discrete Solution Operator Learning for Geometry-Dependent PDEs

Neural operator learning accelerates PDE solution by approximating operators as mappings between continuous function spaces. Yet in many engineering settings, varying geometry induces discrete structural changes, including topological changes, abrupt changes in boundary conditions or boundary types, and changes in the computational domain, which break the smooth-variation premise. Here we introduce Discrete Solution Operator Learning (DiSOL), a complementary paradigm that learns discrete solution procedures rather than continuous function-space operators. DiSOL factorizes the solver into learnable stages that mirror classical discretizations: local contribution encoding, multiscale assembly, and implicit solution reconstruction on an embedded grid, thereby preserving procedure-level consistency while adapting to geometry-dependent discrete structures. Across geometry-dependent Poisson, advection-diffusion, linear elasticity, as well as spatiotemporal heat conduction problems, DiSOL produces stable and accurate predictions under both in-distribution and strongly out-of-distribution geometries, including discontinuous boundaries and topological changes. These results highlight the need for procedural operator representations in geometry-dominated problems and position discrete solution operator learning as a distinct, complementary direction in scientific machine learning.

Exploring Semantic-constrained Adversarial Example with Instruction Uncertainty Reduction

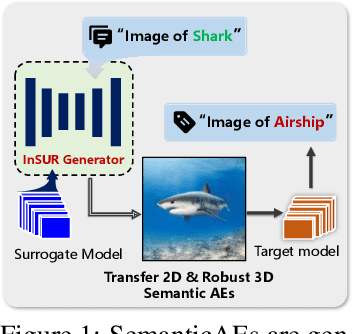
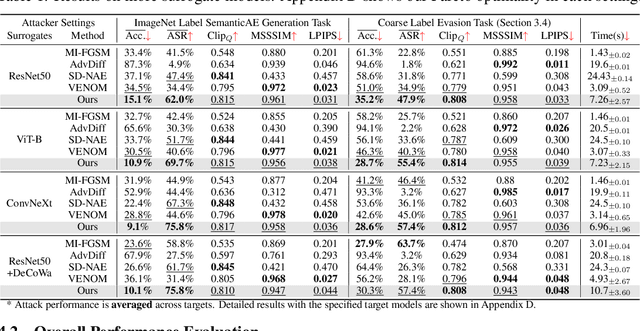
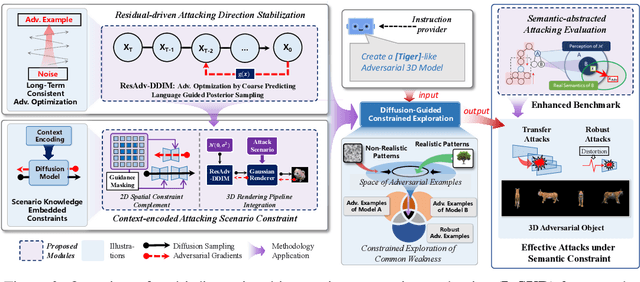
Recently, semantically constrained adversarial examples (SemanticAE), which are directly generated from natural language instructions, have become a promising avenue for future research due to their flexible attacking forms. To generate SemanticAEs, current methods fall short of satisfactory attacking ability as the key underlying factors of semantic uncertainty in human instructions, such as referring diversity, descriptive incompleteness, and boundary ambiguity, have not been fully investigated. To tackle the issues, this paper develops a multi-dimensional instruction uncertainty reduction (InSUR) framework to generate more satisfactory SemanticAE, i.e., transferable, adaptive, and effective. Specifically, in the dimension of the sampling method, we propose the residual-driven attacking direction stabilization to alleviate the unstable adversarial optimization caused by the diversity of language references. By coarsely predicting the language-guided sampling process, the optimization process will be stabilized by the designed ResAdv-DDIM sampler, therefore releasing the transferable and robust adversarial capability of multi-step diffusion models. In task modeling, we propose the context-encoded attacking scenario constraint to supplement the missing knowledge from incomplete human instructions. Guidance masking and renderer integration are proposed to regulate the constraints of 2D/3D SemanticAE, activating stronger scenario-adapted attacks. Moreover, in the dimension of generator evaluation, we propose the semantic-abstracted attacking evaluation enhancement by clarifying the evaluation boundary, facilitating the development of more effective SemanticAE generators. Extensive experiments demonstrate the superiority of the transfer attack performance of InSUR. Moreover, we realize the reference-free generation of semantically constrained 3D adversarial examples for the first time.

LiRA: Linguistic Robust Anchoring for Cross-lingual Large Language Models

As large language models (LLMs) rapidly advance, performance on high-resource languages (e.g., English, Chinese) is nearing saturation, yet remains substantially lower for low-resource languages (e.g., Urdu, Thai) due to limited training data, machine-translation noise, and unstable cross-lingual alignment. We introduce LiRA (Linguistic Robust Anchoring for Large Language Models), a training framework that robustly improves cross-lingual representations under low-resource conditions while jointly strengthening retrieval and reasoning. LiRA comprises two modules: (i) Arca (Anchored Representation Composition Architecture), which anchors low-resource languages to an English semantic space via anchor-based alignment and multi-agent collaborative encoding, preserving geometric stability in a shared embedding space; and (ii) LaSR (Language-coupled Semantic Reasoner), which adds a language-aware lightweight reasoning head with consistency regularization on top of Arca's multilingual representations, unifying the training objective to enhance cross-lingual understanding, retrieval, and reasoning robustness. We further construct and release a multilingual product retrieval dataset covering five Southeast Asian and two South Asian languages. Experiments across low-resource benchmarks (cross-lingual retrieval, semantic similarity, and reasoning) show consistent gains and robustness under few-shot and noise-amplified settings; ablations validate the contribution of both Arca and LaSR. Code will be released on GitHub and the dataset on Hugging Face.

Physics-informed Neural Network Predictive Control for Quadruped Locomotion

This study introduces a unified control framework that addresses the challenge of precise quadruped locomotion with unknown payloads, named as online payload identification-based physics-informed neural network predictive control (OPI-PINNPC). By integrating online payload identification with physics-informed neural networks (PINNs), our approach embeds identified mass parameters directly into the neural network's loss function, ensuring physical consistency while adapting to changing load conditions. The physics-constrained neural representation serves as an efficient surrogate model within our nonlinear model predictive controller, enabling real-time optimization despite the complex dynamics of legged locomotion. Experimental validation on our quadruped robot platform demonstrates 35% improvement in position and orientation tracking accuracy across diverse payload conditions (25-100 kg), with substantially faster convergence compared to previous adaptive control methods. Our framework provides a adaptive solution for maintaining locomotion performance under variable payload conditions without sacrificing computational efficiency.

Finite-PINN: A Physics-Informed Neural Network Architecture for Solving Solid Mechanics Problems with General Geometries

PINN models have demonstrated impressive capabilities in addressing fluid PDE problems, and their potential in solid mechanics is beginning to emerge. This study identifies two key challenges when using PINN to solve general solid mechanics problems. These challenges become evident when comparing the limitations of PINN with the well-established numerical methods commonly used in solid mechanics, such as the finite element method (FEM). Specifically: a) PINN models generate solutions over an infinite domain, which conflicts with the finite boundaries typical of most solid structures; and b) the solution space utilised by PINN is Euclidean, which is inadequate for addressing the complex geometries often present in solid structures. This work proposes a PINN architecture used for general solid mechanics problems, termed the Finite-PINN model. The proposed model aims to effectively address these two challenges while preserving as much of the original implementation of PINN as possible. The unique architecture of the Finite-PINN model addresses these challenges by separating the approximation of stress and displacement fields, and by transforming the solution space from the traditional Euclidean space to a Euclidean-topological joint space. Several case studies presented in this paper demonstrate that the Finite-PINN model provides satisfactory results for a variety of problem types, including both forward and inverse problems, in both 2D and 3D contexts. The developed Finite-PINN model offers a promising tool for addressing general solid mechanics problems, particularly those not yet well-explored in current research.

Graph Sampling for Scalable and Expressive Graph Neural Networks on Homophilic Graphs

Graph Neural Networks (GNNs) excel in many graph machine learning tasks but face challenges when scaling to large networks. GNN transferability allows training on smaller graphs and applying the model to larger ones, but existing methods often rely on random subsampling, leading to disconnected subgraphs and reduced model expressivity. We propose a novel graph sampling algorithm that leverages feature homophily to preserve graph structure. By minimizing the trace of the data correlation matrix, our method better preserves the graph Laplacian's rank than random sampling while achieving lower complexity than spectral methods. Experiments on citation networks show improved performance in preserving graph rank and GNN transferability compared to random sampling.

LoRKD: Low-Rank Knowledge Decomposition for Medical Foundation Models

The widespread adoption of large-scale pre-training techniques has significantly advanced the development of medical foundation models, enabling them to serve as versatile tools across a broad range of medical tasks. However, despite their strong generalization capabilities, medical foundation models pre-trained on large-scale datasets tend to suffer from domain gaps between heterogeneous data, leading to suboptimal performance on specific tasks compared to specialist models, as evidenced by previous studies. In this paper, we explore a new perspective called "Knowledge Decomposition" to improve the performance on specific medical tasks, which deconstructs the foundation model into multiple lightweight expert models, each dedicated to a particular anatomical region, with the aim of enhancing specialization and simultaneously reducing resource consumption. To accomplish the above objective, we propose a novel framework named Low-Rank Knowledge Decomposition (LoRKD), which explicitly separates gradients from different tasks by incorporating low-rank expert modules and efficient knowledge separation convolution. The low-rank expert modules resolve gradient conflicts between heterogeneous data from different anatomical regions, providing strong specialization at lower costs. The efficient knowledge separation convolution significantly improves algorithm efficiency by achieving knowledge separation within a single forward propagation. Extensive experimental results on segmentation and classification tasks demonstrate that our decomposed models not only achieve state-of-the-art performance but also exhibit superior transferability on downstream tasks, even surpassing the original foundation models in task-specific evaluations. The code is available at here.

A MEMS-based terahertz broadband beam steering technique

A multi-level tunable reflection array wide-angle beam scanning method is proposed to address the limited bandwidth and small scanning angle issues of current terahertz beam scanning technology. In this method, a focusing lens and its array are used to achieve terahertz wave spatial beam control, and MEMS mirrors and their arrays are used to achieve wide-angle beam scanning. The 1~3 order terahertz MEMS beam scanning system designed based on this method can extend the mechanical scanning angle of MEMS mirrors by 2~6 times, when tested and verified using an electromagnetic MEMS mirror with a 7mm optical aperture and a scanning angle of 15{\deg} and a D-band terahertz signal source. The experiment shows that the operating bandwidth of the first-order terahertz MEMS beam scanning system is better than 40GHz, the continuous beam scanning angle is about 30{\deg}, the continuous beam scanning cycle response time is about 1.1ms, and the antenna gain is better than 15dBi at 160GHz. This method has been validated for its large bandwidth and scalable scanning angle, and has potential application prospects in terahertz dynamic communication, detection radar, scanning imaging, and other fields.