Spectral Non-Convex Optimization for Dimension Reduction with Hilbert-Schmidt Independence Criterion
Paper and Code
Sep 06, 2019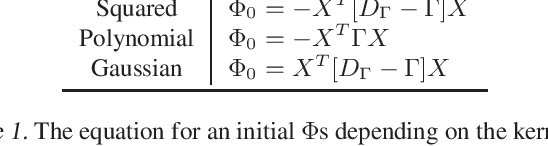


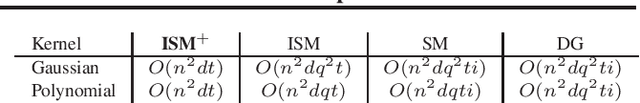
The Hilbert Schmidt Independence Criterion (HSIC) is a kernel dependence measure that has applications in various aspects of machine learning. Conveniently, the objectives of different dimensionality reduction applications using HSIC often reduce to the same optimization problem. However, the nonconvexity of the objective function arising from non-linear kernels poses a serious challenge to optimization efficiency and limits the potential of HSIC-based formulations. As a result, only linear kernels have been computationally tractable in practice. This paper proposes a spectral-based optimization algorithm that extends beyond the linear kernel. The algorithm identifies a family of suitable kernels and provides the first and second-order local guarantees when a fixed point is reached. Furthermore, we propose a principled initialization strategy, thereby removing the need to repeat the algorithm at random initialization points. Compared to state-of-the-art optimization algorithms, our empirical results on real data show a run-time improvement by as much as a factor of $10^5$ while consistently achieving lower cost and classification/clustering errors. The implementation source code is publicly available on https://github.com/endsley.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge