Computing with Categories in Machine Learning

Category theory has been successfully applied in various domains of science, shedding light on universal principles unifying diverse phenomena and thereby enabling knowledge transfer between them. Applications to machine learning have been pursued recently, and yet there is still a gap between abstract mathematical foundations and concrete applications to machine learning tasks. In this paper we introduce DisCoPyro as a categorical structure learning framework, which combines categorical structures (such as symmetric monoidal categories and operads) with amortized variational inference, and can be applied, e.g., in program learning for variational autoencoders. We provide both mathematical foundations and concrete applications together with comparison of experimental performance with other models (e.g., neuro-symbolic models). We speculate that DisCoPyro could ultimately contribute to the development of artificial general intelligence.

A Probabilistic Generative Model of Free Categories

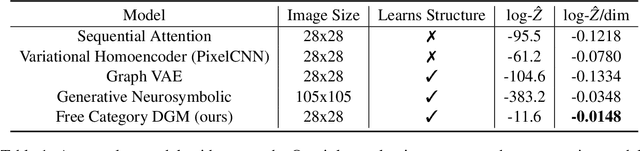
Applied category theory has recently developed libraries for computing with morphisms in interesting categories, while machine learning has developed ways of learning programs in interesting languages. Taking the analogy between categories and languages seriously, this paper defines a probabilistic generative model of morphisms in free monoidal categories over domain-specific generating objects and morphisms. The paper shows how acyclic directed wiring diagrams can model specifications for morphisms, which the model can use to generate morphisms. Amortized variational inference in the generative model then enables learning of parameters (by maximum likelihood) and inference of latent variables (by Bayesian inversion). A concrete experiment shows that the free category prior achieves competitive reconstruction performance on the Omniglot dataset.