Amortized Population Gibbs Samplers with Neural Sufficient Statistics
Paper and Code
Nov 04, 2019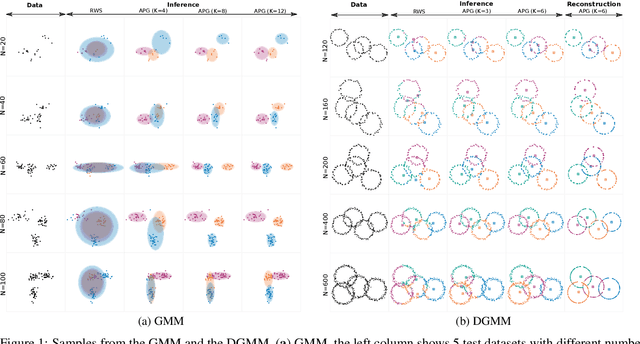
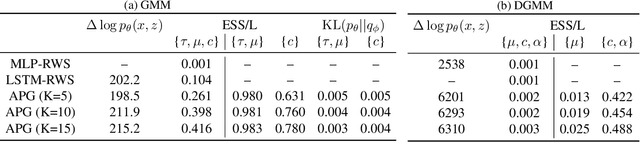
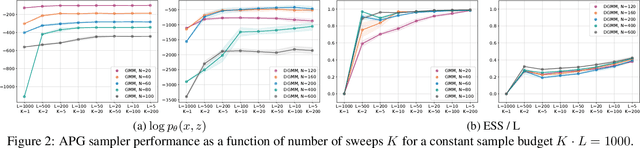

We develop amortized population Gibbs (APG) samplers, a new class of autoencoding variational methods for deep probabilistic models. APG samplers construct high-dimensional proposals by iterating over updates to lower-dimensional blocks of variables. Each conditional update is a neural proposal, which we train by minimizing the inclusive KL divergence relative to the conditional posterior. To appropriately account for the size of the input data, we develop a new parameterization in terms of neural sufficient statistics, resulting in quasi-conjugate variational approximations. Experiments demonstrate that learned proposals converge to the known analytical conditional posterior in conjugate models, and that APG samplers can learn inference networks for highly-structured deep generative models when the conditional posteriors are intractable. Here APG samplers offer a path toward scaling up stochastic variational methods to models in which standard autoencoding architectures fail to produce accurate samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge