Composing Modeling and Inference Operations with Probabilistic Program Combinators
Paper and Code
Nov 29, 2018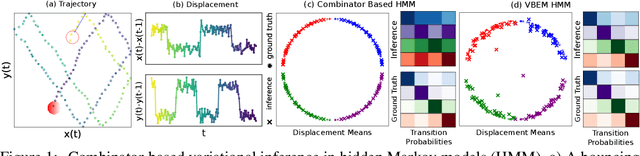

Probabilistic programs with dynamic computation graphs can define measures over sample spaces with unbounded dimensionality, which constitute programmatic analogues to Bayesian nonparametrics. Owing to the generality of this model class, inference relies on `black-box' Monte Carlo methods that are often not able to take advantage of conditional independence and exchangeability, which have historically been the cornerstones of efficient inference. We here seek to develop a `middle ground' between probabilistic models with fully dynamic and fully static computation graphs. To this end, we introduce a combinator library for the Probabilistic Torch framework. Combinators are functions that accept models and return transformed models. We assume that models are dynamic, but that model composition is static, in the sense that combinator application takes place prior to evaluating the model on data. Combinators provide primitives for both model and inference composition. Model combinators take the form of classic functional programming constructs such as map and reduce. These constructs define a computation graph at a coarsened level of representation, in which nodes correspond to models, rather than individual variables. Inference combinators implement operations such as importance resampling and application of a transition kernel, which alter the evaluation strategy for a model whilst preserving proper weighting. Owing to this property, models defined using combinators can be trained using stochastic methods that optimize either variational or wake-sleep style objectives. As a validation of this principle, we use combinators to implement black box inference for hidden Markov models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge