GOLD: Generalized Knowledge Distillation via Out-of-Distribution-Guided Language Data Generation

Knowledge distillation from LLMs is essential for the efficient deployment of language models. Prior works have proposed data generation using LLMs for preparing distilled models. We argue that generating data with LLMs is prone to sampling mainly from the center of original content distribution. This limitation hinders the distilled model from learning the true underlying data distribution and to forget the tails of the distributions (samples with lower probability). To this end, we propose GOLD, a task-agnostic data generation and knowledge distillation framework, which employs an iterative out-of-distribution-guided feedback mechanism for the LLM. As a result, the generated data improves the generalizability of distilled models. An energy-based OOD evaluation approach is also introduced to deal with noisy generated data. Our extensive experiments on 10 different classification and sequence-to-sequence tasks in NLP show that GOLD respectively outperforms prior arts and the LLM with an average improvement of 5% and 14%. We will also show that the proposed method is applicable to less explored and novel tasks. The code is available.

Flexible Diffusion Modeling of Long Videos

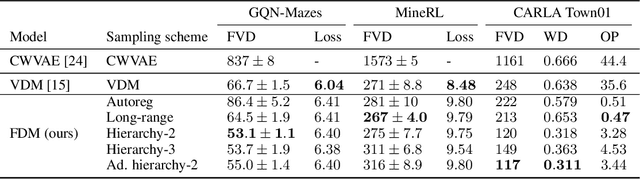
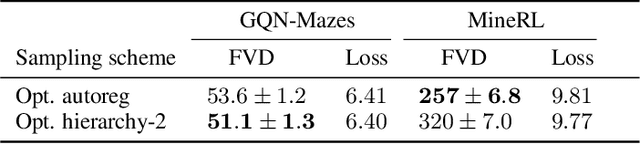
We present a framework for video modeling based on denoising diffusion probabilistic models that produces long-duration video completions in a variety of realistic environments. We introduce a generative model that can at test-time sample any arbitrary subset of video frames conditioned on any other subset and present an architecture adapted for this purpose. Doing so allows us to efficiently compare and optimize a variety of schedules for the order in which frames in a long video are sampled and use selective sparse and long-range conditioning on previously sampled frames. We demonstrate improved video modeling over prior work on a number of datasets and sample temporally coherent videos over 25 minutes in length. We additionally release a new video modeling dataset and semantically meaningful metrics based on videos generated in the CARLA self-driving car simulator.

Beyond Simple Meta-Learning: Multi-Purpose Models for Multi-Domain, Active and Continual Few-Shot Learning

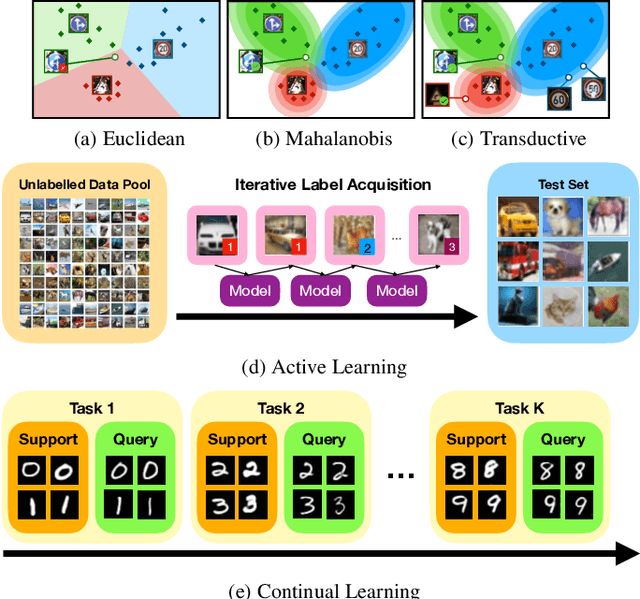
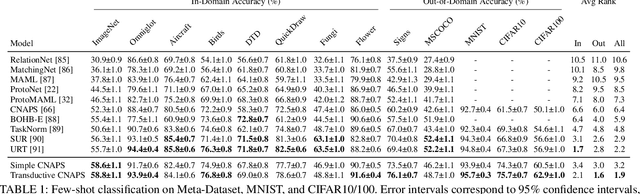
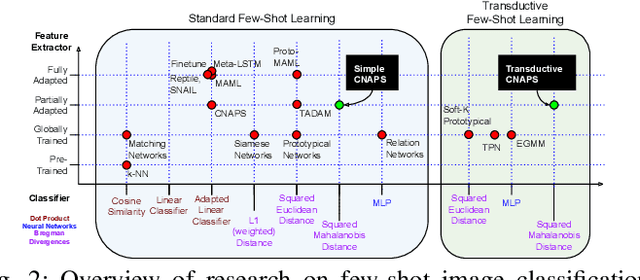
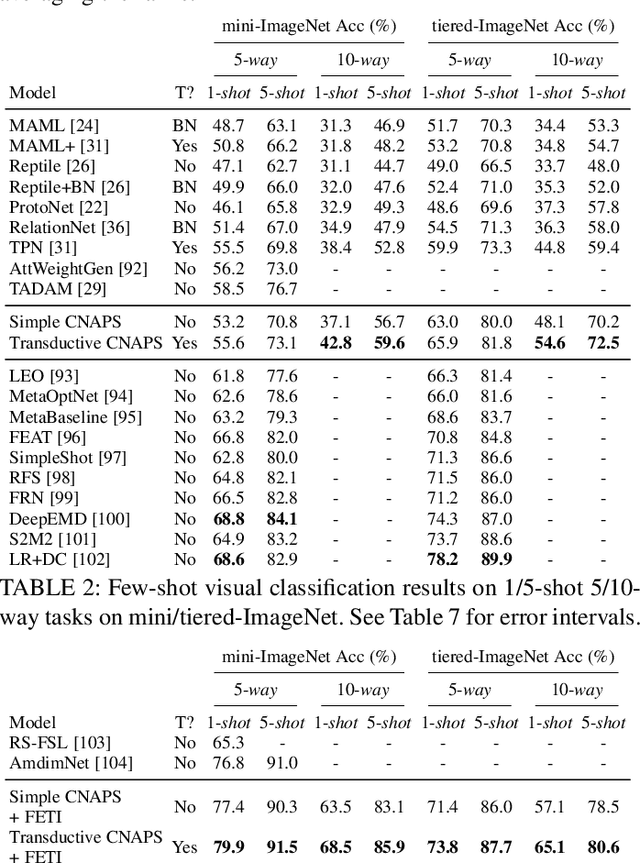
Modern deep learning requires large-scale extensively labelled datasets for training. Few-shot learning aims to alleviate this issue by learning effectively from few labelled examples. In previously proposed few-shot visual classifiers, it is assumed that the feature manifold, where classifier decisions are made, has uncorrelated feature dimensions and uniform feature variance. In this work, we focus on addressing the limitations arising from this assumption by proposing a variance-sensitive class of models that operates in a low-label regime. The first method, Simple CNAPS, employs a hierarchically regularized Mahalanobis-distance based classifier combined with a state of the art neural adaptive feature extractor to achieve strong performance on Meta-Dataset, mini-ImageNet and tiered-ImageNet benchmarks. We further extend this approach to a transductive learning setting, proposing Transductive CNAPS. This transductive method combines a soft k-means parameter refinement procedure with a two-step task encoder to achieve improved test-time classification accuracy using unlabelled data. Transductive CNAPS achieves state of the art performance on Meta-Dataset. Finally, we explore the use of our methods (Simple and Transductive) for "out of the box" continual and active learning. Extensive experiments on large scale benchmarks illustrate robustness and versatility of this, relatively speaking, simple class of models. All trained model checkpoints and corresponding source codes have been made publicly available.

Proof of the impossibility of probabilistic induction

In this short note I restate and simplify the proof of the impossibility of probabilistic induction from Popper (1992). Other proofs are possible (cf. Popper (1985)).

q-Paths: Generalizing the Geometric Annealing Path using Power Means

Many common machine learning methods involve the geometric annealing path, a sequence of intermediate densities between two distributions of interest constructed using the geometric average. While alternatives such as the moment-averaging path have demonstrated performance gains in some settings, their practical applicability remains limited by exponential family endpoint assumptions and a lack of closed form energy function. In this work, we introduce $q$-paths, a family of paths which is derived from a generalized notion of the mean, includes the geometric and arithmetic mixtures as special cases, and admits a simple closed form involving the deformed logarithm function from nonextensive thermodynamics. Following previous analysis of the geometric path, we interpret our $q$-paths as corresponding to a $q$-exponential family of distributions, and provide a variational representation of intermediate densities as minimizing a mixture of $\alpha$-divergences to the endpoints. We show that small deviations away from the geometric path yield empirical gains for Bayesian inference using Sequential Monte Carlo and generative model evaluation using Annealed Importance Sampling.

Differentiable Particle Filtering without Modifying the Forward Pass

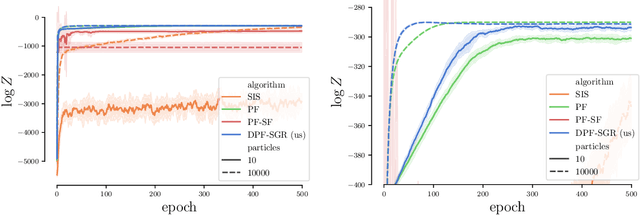
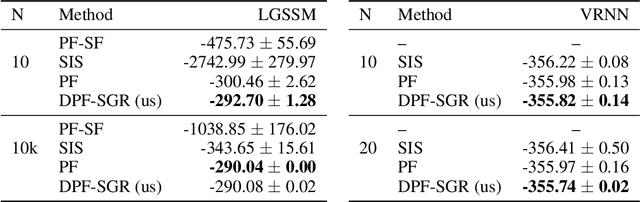
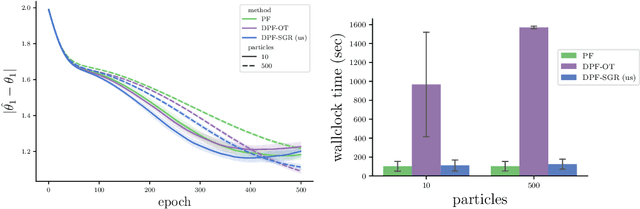
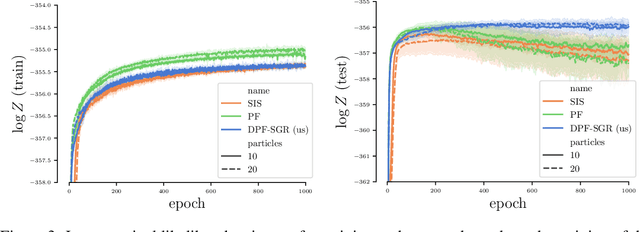
In recent years particle filters have being used as components in systems optimized end-to-end with gradient descent. However, the resampling step in a particle filter is not differentiable, which biases gradients and interferes with optimization. To remedy this problem, several differentiable variants of resampling have been proposed, all of which modify the behavior of the particle filter in significant and potentially undesirable ways. In this paper, we show how to obtain unbiased estimators of the gradient of the marginal likelihood by only modifying messages used in backpropagation, leaving the standard forward pass of a particle filter unchanged. Our method is simple to implement, has a low computational overhead, does not introduce additional hyperparameters, and extends to derivatives of higher orders. We call it stop-gradient resampling, since it can easily be implemented with automatic differentiation libraries using the stop-gradient operator instead of explicitly modifying the backward messages.

Annealed Importance Sampling with q-Paths

Annealed importance sampling (AIS) is the gold standard for estimating partition functions or marginal likelihoods, corresponding to importance sampling over a path of distributions between a tractable base and an unnormalized target. While AIS yields an unbiased estimator for any path, existing literature has been primarily limited to the geometric mixture or moment-averaged paths associated with the exponential family and KL divergence. We explore AIS using $q$-paths, which include the geometric path as a special case and are related to the homogeneous power mean, deformed exponential family, and $\alpha$-divergence.

Gaussian Process Bandit Optimization of the Thermodynamic Variational Objective

Achieving the full promise of the Thermodynamic Variational Objective (TVO), a recently proposed variational lower bound on the log evidence involving a one-dimensional Riemann integral approximation, requires choosing a "schedule" of sorted discretization points. This paper introduces a bespoke Gaussian process bandit optimization method for automatically choosing these points. Our approach not only automates their one-time selection, but also dynamically adapts their positions over the course of optimization, leading to improved model learning and inference. We provide theoretical guarantees that our bandit optimization converges to the regret-minimizing choice of integration points. Empirical validation of our algorithm is provided in terms of improved learning and inference in Variational Autoencoders and Sigmoid Belief Networks.

All in the Exponential Family: Bregman Duality in Thermodynamic Variational Inference

The recently proposed Thermodynamic Variational Objective (TVO) leverages thermodynamic integration to provide a family of variational inference objectives, which both tighten and generalize the ubiquitous Evidence Lower Bound (ELBO). However, the tightness of TVO bounds was not previously known, an expensive grid search was used to choose a "schedule" of intermediate distributions, and model learning suffered with ostensibly tighter bounds. In this work, we propose an exponential family interpretation of the geometric mixture curve underlying the TVO and various path sampling methods, which allows us to characterize the gap in TVO likelihood bounds as a sum of KL divergences. We propose to choose intermediate distributions using equal spacing in the moment parameters of our exponential family, which matches grid search performance and allows the schedule to adaptively update over the course of training. Finally, we derive a doubly reparameterized gradient estimator which improves model learning and allows the TVO to benefit from more refined bounds. To further contextualize our contributions, we provide a unified framework for understanding thermodynamic integration and the TVO using Taylor series remainders.

Planning as Inference in Epidemiological Models

In this work we demonstrate how existing software tools can be used to automate parts of infectious disease-control policy-making via performing inference in existing epidemiological dynamics models. The kind of inference tasks undertaken include computing, for planning purposes, the posterior distribution over putatively controllable, via direct policy-making choices, simulation model parameters that give rise to acceptable disease progression outcomes. Neither the full capabilities of such inference automation software tools nor their utility for planning is widely disseminated at the current time. Timely gains in understanding about these tools and how they can be used may lead to more fine-grained and less economically damaging policy prescriptions, particularly during the current COVID-19 pandemic.