Stochastic uncertainty analysis of gravity gradient tensor components and their combinations

Full tensor gravity (FTG) devices provide up to five independent components of the gravity gradient tensor. However, we do not yet have a quantitative understanding of which tensor components or combinations of components are more important to recover a subsurface density model by gravity inversion. This is mainly because different components may be more appropriate in different scenarios or purposes. Knowledge of these components in different environments can aid with selection of optimal selection of component combinations. In this work, we propose to apply stochastic inversion to assess the uncertainty of gravity gradient tensor components and their combinations. The method is therefore a quantitative approach. The applied method here is based on the geostatistical inversion (Gaussian process regression) concept using cokriging. The cokriging variances (variance function of the GP) are found to be a useful indicator for distinguishing the gravity gradient tensor components. This approach is applied to the New Found dataset to demonstrate its effectiveness in real-world applications.

Active Distance-Based Clustering using K-medoids

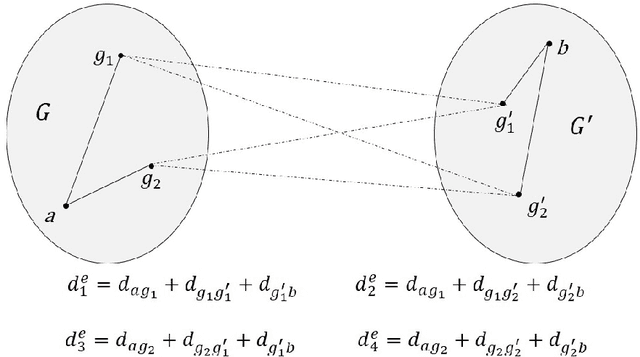
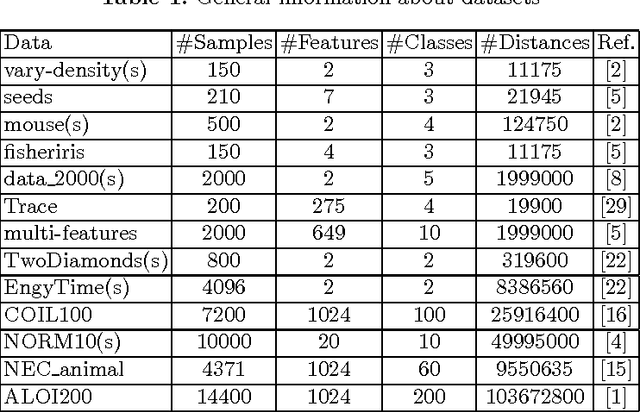
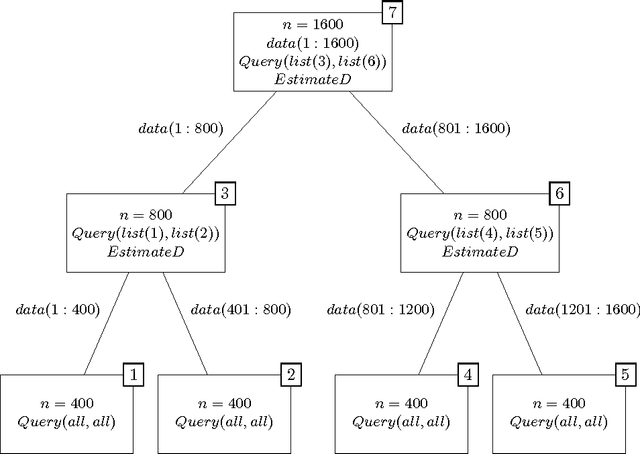
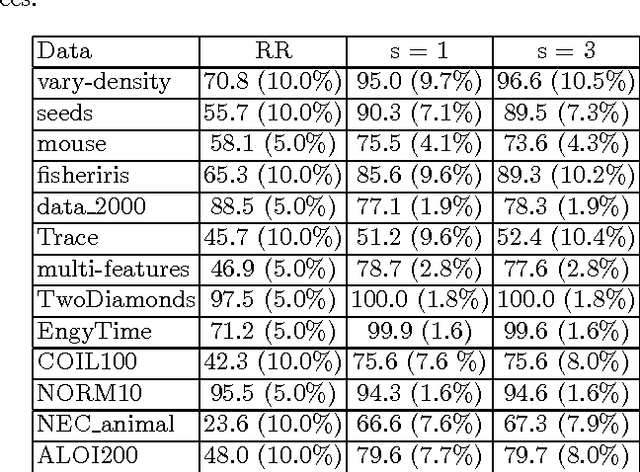
k-medoids algorithm is a partitional, centroid-based clustering algorithm which uses pairwise distances of data points and tries to directly decompose the dataset with $n$ points into a set of $k$ disjoint clusters. However, k-medoids itself requires all distances between data points that are not so easy to get in many applications. In this paper, we introduce a new method which requires only a small proportion of the whole set of distances and makes an effort to estimate an upper-bound for unknown distances using the inquired ones. This algorithm makes use of the triangle inequality to calculate an upper-bound estimation of the unknown distances. Our method is built upon a recursive approach to cluster objects and to choose some points actively from each bunch of data and acquire the distances between these prominent points from oracle. Experimental results show that the proposed method using only a small subset of the distances can find proper clustering on many real-world and synthetic datasets.