Distributed Maximization of "Submodular plus Diversity" Functions for Multi-label Feature Selection on Huge Datasets

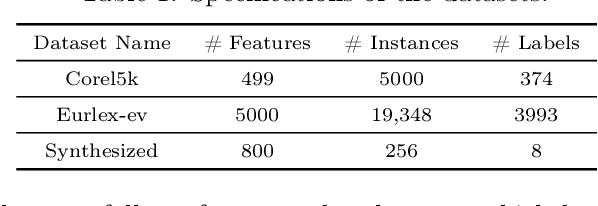
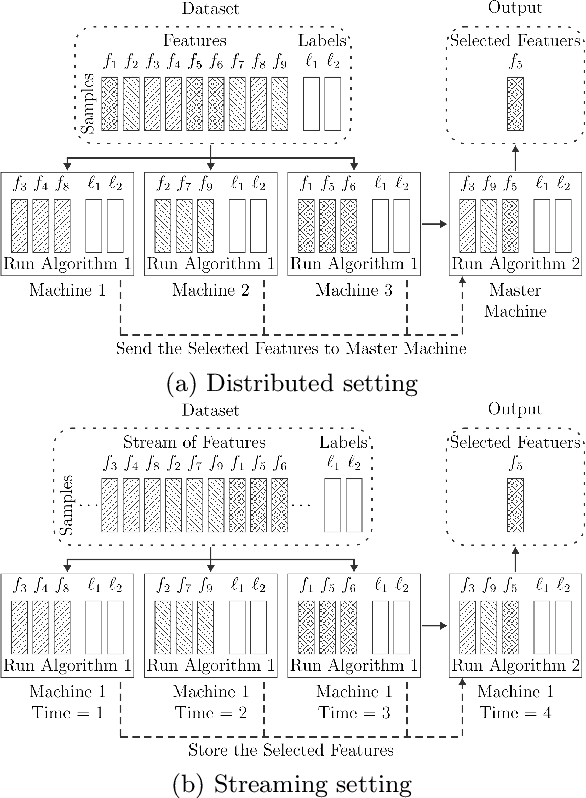
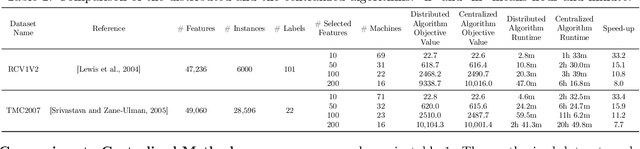
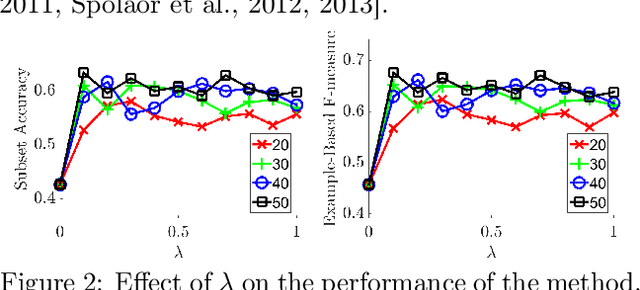
There are many problems in machine learning and data mining which are equivalent to selecting a non-redundant, high "quality" set of objects. Recommender systems, feature selection, and data summarization are among many applications of this. In this paper, we consider this problem as an optimization problem that seeks to maximize the sum of a sum-sum diversity function and a non-negative monotone submodular function. The diversity function addresses the redundancy, and the submodular function controls the predictive quality. We consider the problem in big data settings (in other words, distributed and streaming settings) where the data cannot be stored on a single machine or the process time is too high for a single machine. We show that a greedy algorithm achieves a constant factor approximation of the optimal solution in these settings. Moreover, we formulate the multi-label feature selection problem as such an optimization problem. This formulation combined with our algorithm leads to the first distributed multi-label feature selection method. We compare the performance of this method with centralized multi-label feature selection methods in the literature, and we show that its performance is comparable or in some cases is even better than current centralized multi-label feature selection methods.