On Approximability of $\ell_2^2$ Min-Sum Clustering

The $\ell_2^2$ min-sum $k$-clustering problem is to partition an input set into clusters $C_1,\ldots,C_k$ to minimize $\sum_{i=1}^k\sum_{p,q\in C_i}\|p-q\|_2^2$. Although $\ell_2^2$ min-sum $k$-clustering is NP-hard, it is not known whether it is NP-hard to approximate $\ell_2^2$ min-sum $k$-clustering beyond a certain factor. In this paper, we give the first hardness-of-approximation result for the $\ell_2^2$ min-sum $k$-clustering problem. We show that it is NP-hard to approximate the objective to a factor better than $1.056$ and moreover, assuming a balanced variant of the Johnson Coverage Hypothesis, it is NP-hard to approximate the objective to a factor better than 1.327. We then complement our hardness result by giving the first $(1+\varepsilon)$-coreset construction for $\ell_2^2$ min-sum $k$-clustering. Our coreset uses $\mathcal{O}\left(k^{\varepsilon^{-4}}\right)$ space and can be leveraged to achieve a polynomial-time approximation scheme with runtime $nd\cdot f(k,\varepsilon^{-1})$, where $d$ is the underlying dimension of the input dataset and $f$ is a fixed function. Finally, we consider a learning-augmented setting, where the algorithm has access to an oracle that outputs a label $i\in[k]$ for input point, thereby implicitly partitioning the input dataset into $k$ clusters that induce an approximately optimal solution, up to some amount of adversarial error $\alpha\in\left[0,\frac{1}{2}\right)$. We give a polynomial-time algorithm that outputs a $\frac{1+\gamma\alpha}{(1-\alpha)^2}$-approximation to $\ell_2^2$ min-sum $k$-clustering, for a fixed constant $\gamma>0$.

Can You Solve Closest String Faster than Exhaustive Search?

We study the fundamental problem of finding the best string to represent a given set, in the form of the Closest String problem: Given a set $X \subseteq \Sigma^d$ of $n$ strings, find the string $x^*$ minimizing the radius of the smallest Hamming ball around $x^*$ that encloses all the strings in $X$. In this paper, we investigate whether the Closest String problem admits algorithms that are faster than the trivial exhaustive search algorithm. We obtain the following results for the two natural versions of the problem: $\bullet$ In the continuous Closest String problem, the goal is to find the solution string $x^*$ anywhere in $\Sigma^d$. For binary strings, the exhaustive search algorithm runs in time $O(2^d poly(nd))$ and we prove that it cannot be improved to time $O(2^{(1-\epsilon) d} poly(nd))$, for any $\epsilon > 0$, unless the Strong Exponential Time Hypothesis fails. $\bullet$ In the discrete Closest String problem, $x^*$ is required to be in the input set $X$. While this problem is clearly in polynomial time, its fine-grained complexity has been pinpointed to be quadratic time $n^{2 \pm o(1)}$ whenever the dimension is $\omega(\log n) < d < n^{o(1)}$. We complement this known hardness result with new algorithms, proving essentially that whenever $d$ falls out of this hard range, the discrete Closest String problem can be solved faster than exhaustive search. In the small-$d$ regime, our algorithm is based on a novel application of the inclusion-exclusion principle. Interestingly, all of our results apply (and some are even stronger) to the natural dual of the Closest String problem, called the Remotest String problem, where the task is to find a string maximizing the Hamming distance to all the strings in $X$.

Impossibility of Depth Reduction in Explainable Clustering

Over the last few years Explainable Clustering has gathered a lot of attention. Dasgupta et al. [ICML'20] initiated the study of explainable k-means and k-median clustering problems where the explanation is captured by a threshold decision tree which partitions the space at each node using axis parallel hyperplanes. Recently, Laber et al. [Pattern Recognition'23] made a case to consider the depth of the decision tree as an additional complexity measure of interest. In this work, we prove that even when the input points are in the Euclidean plane, then any depth reduction in the explanation incurs unbounded loss in the k-means and k-median cost. Formally, we show that there exists a data set X in the Euclidean plane, for which there is a decision tree of depth k-1 whose k-means/k-median cost matches the optimal clustering cost of X, but every decision tree of depth less than k-1 has unbounded cost w.r.t. the optimal cost of clustering. We extend our results to the k-center objective as well, albeit with weaker guarantees.

Clustering Categorical Data: Soft Rounding k-modes

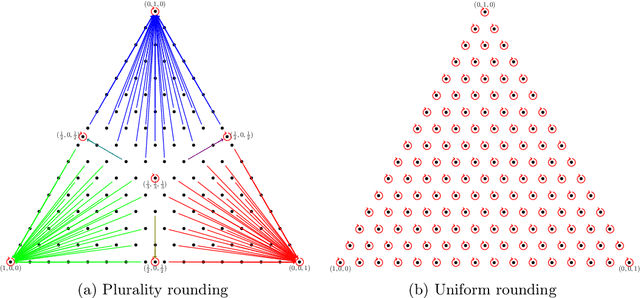
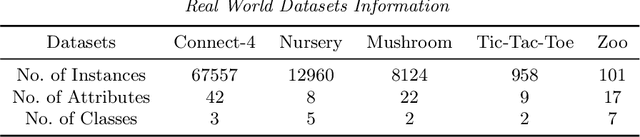
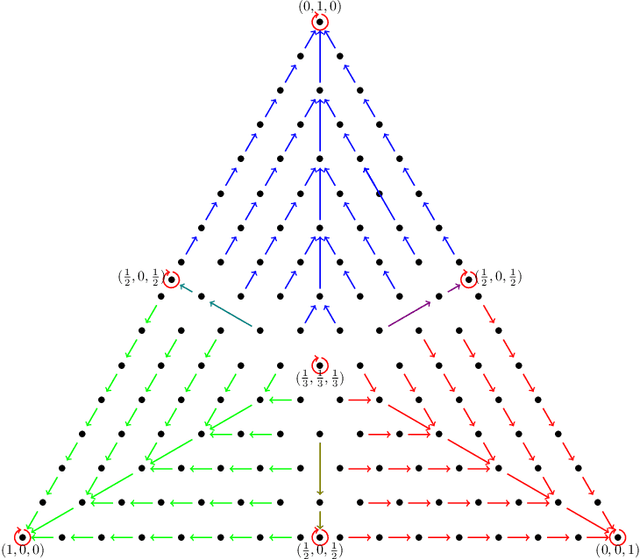
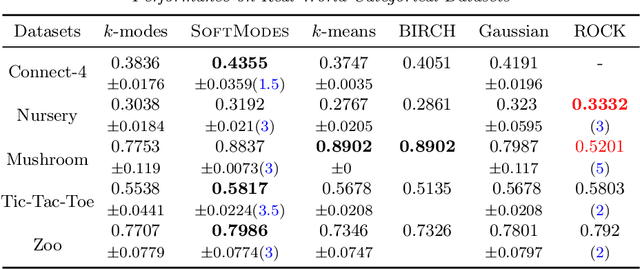
Over the last three decades, researchers have intensively explored various clustering tools for categorical data analysis. Despite the proposal of various clustering algorithms, the classical k-modes algorithm remains a popular choice for unsupervised learning of categorical data. Surprisingly, our first insight is that in a natural generative block model, the k-modes algorithm performs poorly for a large range of parameters. We remedy this issue by proposing a soft rounding variant of the k-modes algorithm (SoftModes) and theoretically prove that our variant addresses the drawbacks of the k-modes algorithm in the generative model. Finally, we empirically verify that SoftModes performs well on both synthetic and real-world datasets.

On Complexity of 1-Center in Various Metrics

We consider the classic 1-center problem: Given a set P of n points in a metric space find the point in P that minimizes the maximum distance to the other points of P. We study the complexity of this problem in d-dimensional $\ell_p$-metrics and in edit and Ulam metrics over strings of length d. Our results for the 1-center problem may be classified based on d as follows. $\bullet$ Small d: We provide the first linear-time algorithm for 1-center problem in fixed-dimensional $\ell_1$ metrics. On the other hand, assuming the hitting set conjecture (HSC), we show that when $d=\omega(\log n)$, no subquadratic algorithm can solve 1-center problem in any of the $\ell_p$-metrics, or in edit or Ulam metrics. $\bullet$ Large d. When $d=\Omega(n)$, we extend our conditional lower bound to rule out sub quartic algorithms for 1-center problem in edit metric (assuming Quantified SETH). On the other hand, we give a $(1+\epsilon)$-approximation for 1-center in Ulam metric with running time $\tilde{O_{\epsilon}}(nd+n^2\sqrt{d})$. We also strengthen some of the above lower bounds by allowing approximations or by reducing the dimension d, but only against a weaker class of algorithms which list all requisite solutions. Moreover, we extend one of our hardness results to rule out subquartic algorithms for the well-studied 1-median problem in the edit metric, where given a set of n strings each of length n, the goal is to find a string in the set that minimizes the sum of the edit distances to the rest of the strings in the set.

On Efficient Low Distortion Ultrametric Embedding

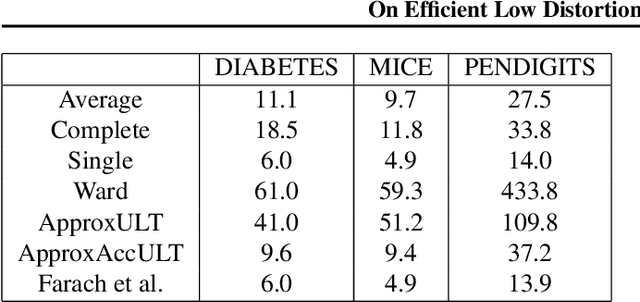
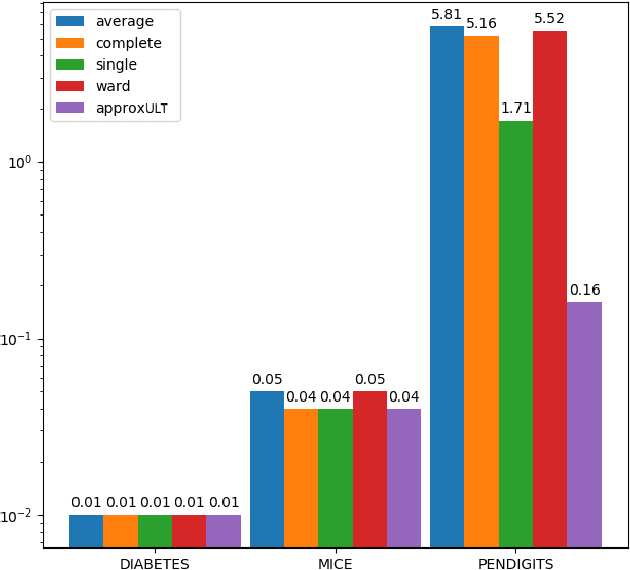
A classic problem in unsupervised learning and data analysis is to find simpler and easy-to-visualize representations of the data that preserve its essential properties. A widely-used method to preserve the underlying hierarchical structure of the data while reducing its complexity is to find an embedding of the data into a tree or an ultrametric. The most popular algorithms for this task are the classic linkage algorithms (single, average, or complete). However, these methods on a data set of $n$ points in $\Omega(\log n)$ dimensions exhibit a quite prohibitive running time of $\Theta(n^2)$. In this paper, we provide a new algorithm which takes as input a set of points $P$ in $\mathbb{R}^d$, and for every $c\ge 1$, runs in time $n^{1+\frac{\rho}{c^2}}$ (for some universal constant $\rho>1$) to output an ultrametric $\Delta$ such that for any two points $u,v$ in $P$, we have $\Delta(u,v)$ is within a multiplicative factor of $5c$ to the distance between $u$ and $v$ in the "best" ultrametric representation of $P$. Here, the best ultrametric is the ultrametric $\tilde\Delta$ that minimizes the maximum distance distortion with respect to the $\ell_2$ distance, namely that minimizes $\underset{u,v \in P}{\max}\ \frac{\tilde\Delta(u,v)}{\|u-v\|_2}$. We complement the above result by showing that under popular complexity theoretic assumptions, for every constant $\varepsilon>0$, no algorithm with running time $n^{2-\varepsilon}$ can distinguish between inputs in $\ell_\infty$-metric that admit isometric embedding and those that incur a distortion of $\frac{3}{2}$. Finally, we present empirical evaluation on classic machine learning datasets and show that the output of our algorithm is comparable to the output of the linkage algorithms while achieving a much faster running time.